基本図形を変形する

  1. ホーム
  2. 壁紙アート
  3. 基本図形を変形する

別記事「基本図形の形状を考える」では、17種類の壁紙群それぞれに対して、ボロノイ図を用いてその基本図形の形状としてどんなものが考えられるのかをみてみました。その結果、基本図形の形状としては三角形、四角形、五角形、六角形が現れました。

ここでは、次のステップとして、基本図形の各辺の形を変形することを考えていきます。これにより、壁紙アートのバリエーションを増やすことができます。特にエッシャーが描いたような絵を自分でもプログラミングして描いていくことができるようになります。

なお、この記事は、書籍「エッシャー・マジック―だまし絵の世界を数理で読み解く」の3.1節から3.3節まで（p.39~p.50）を参考にして考えています。

変形する際のルール

壁紙アートは、基本図形を準備し、それを回転させたり、反転させたりしながら敷き詰めていくことで描きます。つまり、隣り合う基本図形同士の接する辺がぴったりとはまる必要があります。別記事「基本図形の形状を考える」では、17種類の壁紙群についてそれぞれ隣り合う基本図形の各辺にラベル付けをして、どの辺とどの辺が重なるのかを見てきました。変形を考える場合、さらに重なる辺同士の向きを考える必要があります。

これらは、書籍「エッシャー・マジック―だまし絵の世界を数理で読み解く」の3.1節（p.40~p.44）にまとめてありますので、以下はそれを参考に解説していきます。

隣り合う基本図形の辺をはさんで現れる向きとラベルの組合せパターンは、4通りに分類でき、それぞれに許される変形が図に示すように決まります。

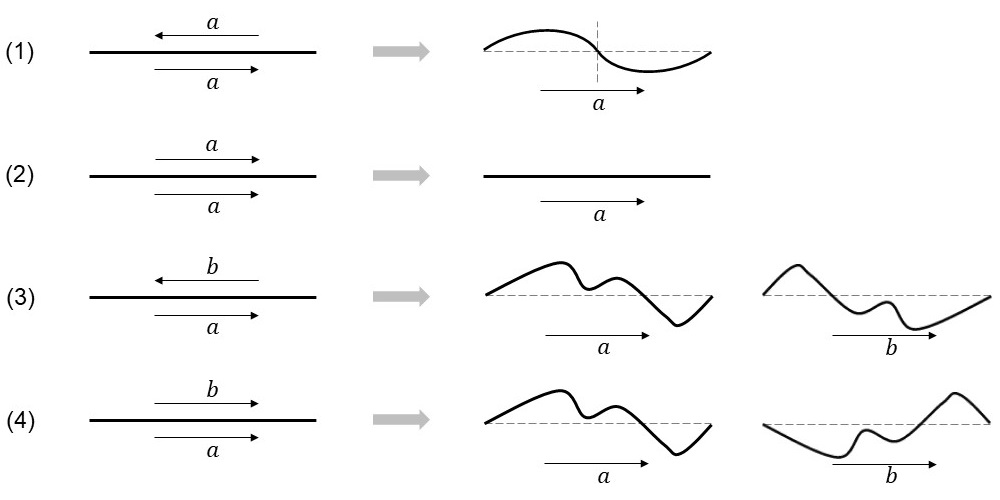
重なる辺のラベルと向きの組合せによって特徴づけられる変形の自由度

（１）両側のラベルが同じで向きが異なるとき、重なる辺は中点に関して点対称な変形が可能です。

（２）両側のラベルが同じで向きも同じとき、この辺は変形できず、線分のみとなります。

（３）両側のラベルが異なり、向きも異なるとき、辺\(a\)は自由に変形することができ、辺\(b\)は辺\(a\)を上下と左右とを反転した形になります。

（４）両側のラベルが異なり、向きは同じとき、辺\(a\)は自由に変形することができ、辺\(b\)は辺\(a\)を上下に反転した形になります。

ただし、上記の変形をする際は、以下を注意する必要があります。

（i）変形した辺同士が交差してはいけない。

（ii）辺の変形は、その両側の基本図形の外へはみ出してはいけない。

（iii）頂点の位置を動かしてはいけない。

変形してみる

では、17種類の壁紙群それぞれの基本図形を変形してみたいと思います。なお、ここでは別記事「渦巻き図形」で作成したプログラムを再利用します。具体的には、基本図形を生成する関数として渦巻きを生成するものではなく、各辺を変形するものに置き換えて利用していきます。

P1群の基本図形の変形

P1群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P1群の基本図形に対する辺のラベルと向き

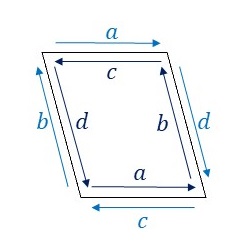
辺\(a\)と辺\(c\)、および辺\(b\)と辺\(d\)がそれぞれ異なる向きに重なっています。つまり、注意点（i）、（ii）、（iii）を考慮して辺\(a\)を変形し、辺\(c\)は、変形した辺\(a\)を上下左右反転した形状に変形します。また辺\(b\)と辺\(d\)についても同じように変形することで、隣り合う基本図形同士を重ねることなくP1群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってP1群の基本図形を下図のように変形してみました。

P1群の基本図形の変形

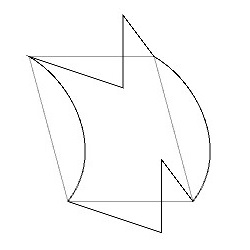
この変形した基本図形をP1群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

Ｐ1群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（P1）」に記載しているプログラムコードのうち、makeRecurParallelogram関数を下記のtransformParallelogram関数に置き換えたものになります。（もう少し細かい話をすると、makeTileP1関数内のmakeRecurParallelogram関数をtransformParallelogram関数に変更する必要があります。また、drawTiling関数内の記述していた「格子点を描く」部分はコメントアウトしています。）

// 平行四辺形を変形する関数（基本図形）
PShape transformParallelogram(){
  
  PVector[] v = new PVector[4]; // 平行四辺形の頂点
  PShape parallelogram = createShape();

  v[0] = base[0].copy();
  v[0].sub(base[1]);
  v[0].mult(-scalar / 2.0);
  v[1] = base[0].copy();
  v[1].add(base[1]);
  v[1].mult(scalar / 2.0);
  v[2] = base[0].copy();
  v[2].sub(base[1]);
  v[2].mult(scalar / 2.0);
  v[3] = base[0].copy();
  v[3].add(base[1]);
  v[3].mult(-scalar / 2.0);

  // 平行四辺形を変形する
  parallelogram.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  // 辺aをジグザグに変形する
  parallelogram.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, 1.0/4.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, -1.0/3.0); 
  parallelogram.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  parallelogram.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  parallelogram.vertex(v[1].x, v[1].y);
  // 辺bをベジエ曲線で変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 3.0/4.0, 1.0/4.0); 
  parallelogram.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[2].x, v[2].y);
  // 辺cを辺aと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[3], v[2], 3.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[3], v[2], 3.0/4.0, -1.0/3.0);
  parallelogram.vertex(auxiliary_point[1].x, auxiliary_point[1].y);  
  parallelogram.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  parallelogram.vertex(v[3].x, v[3].y);
  // 辺dを辺bと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[3], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[3], 3.0/4.0, 1.0/4.0);
  parallelogram.bezierVertex(auxiliary_point[1].x, auxiliary_point[1].y, auxiliary_point[0].x, auxiliary_point[0].y, v[0].x, v[0].y);  

  parallelogram.endShape();
  
  return parallelogram;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

P2群の基本図形の変形

P2群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P2群の基本図形に対する辺のラベルと向き

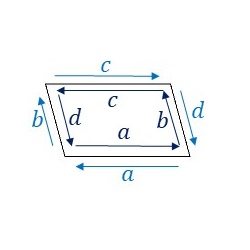
辺\(a\)と辺\(c\)についてはそれぞれ両側のラベルが同じで向きが異なっていますので、中点に関して点対称な変形を行います。辺\(b\)と辺\(d\)は異なる向きに重なっています。つまり、辺\(b\)を適当に変形したあと、辺\(d\)は、変形した辺\(b\)を上下左右反転した形状に変形します。そうすると、隣り合う基本図形同士を重ねることなくP2群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってP2群の基本図形を下図のように変形してみました。

P2群の基本図形の変形

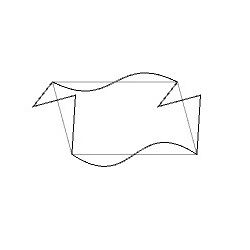
この変形した基本図形をP2群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

Ｐ2群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（P2）」に記載しているプログラムコードのうち、makeRecurParallelogram関数を下記のtransformParallelogram関数に置き換えたものになります。

// 平行四辺形を変形する関数（基本図形）
PShape transformParallelogram(){
  
  PVector[] v = new PVector[4]; // 平行四辺形の頂点
  PShape parallelogram = createShape();

  v[0] = base[0].copy();
  v[0].sub(base[1]);
  v[0].mult(-scalar / 2.0);
  v[1] = base[0].copy();
  v[1].add(base[1]);
  v[1].mult(scalar / 2.0);
  v[2] = base[0].copy();
  v[2].mult(scalar / 2.0);
  v[3] = base[0].copy();
  v[3].mult(-scalar / 2.0);

  // 平行四辺形を変形する
  parallelogram.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  // 辺aをベジエ曲線で中点で対称になるように変形する
  parallelogram.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 1.0/2.0, 1.0/3.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 1.0/2.0, -1.0/3.0); 
  parallelogram.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[1].x, v[1].y);
  // 辺bをジグザクに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 3.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 3.0/4.0, -1.0/3.0);
  parallelogram.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  parallelogram.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  parallelogram.vertex(v[2].x, v[2].y); 
  // 辺cをベジエ曲線で中点で対称になるように変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 1.0/2.0, 1.0/4.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 1.0/2.0, -1.0/4.0); 
  parallelogram.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[3].x, v[3].y);
  // 辺dを辺bと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[3], 3.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[3], 3.0/4.0, -1.0/3.0);
  parallelogram.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  parallelogram.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  parallelogram.vertex(v[0].x, v[0].y);
  
  parallelogram.endShape();
  
  return parallelogram;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

PM群の基本図形の変形

PM群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

PM群の基本図形に対する辺のラベルと向き

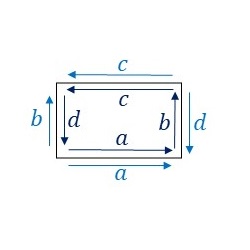
辺\(a\)と辺\(c\)についてはそれぞれ両側のラベルが同じで向きも同じになっていますので、変形できず、線分となります。辺\(b\)と辺\(d\)は異なる向きに重なっています。つまり、辺\(b\)を適当に変形したあと、辺\(d\)は、変形した辺\(b\)を上下左右反転した形状に変形します。そうすると、隣り合う基本図形同士を重ねることなくPM群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってPM群の基本図形を下図のように変形してみました。

PM群の基本図形の変形

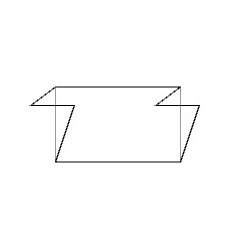
この変形した基本図形をPM群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

ＰM群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（PM）」に記載しているプログラムコードのうち、makeRecurRectangle関数を下記のtransformRectangle関数に置き換えたものになります。

// 長方形を変形する関数（基本図形）
PShape transformRectangle(){
  
  PVector[] v = new PVector[4]; // 長方形の頂点
  PShape rect = createShape();

  v[0] = base[0].copy();
  v[0].sub(base[1]);
  v[0].mult(-scalar / 2.0);
  v[1] = base[0].copy();
  v[1].add(base[1]);
  v[1].mult(scalar / 2.0);
  v[2] = base[0].copy();
  v[2].mult(scalar / 2.0);
  v[3] = base[0].copy();
  v[3].mult(-scalar / 2.0);

  // 長方形を変形する
  rect.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  // 辺aは変形できず、直線のみ。
  rect.vertex(v[0].x, v[0].y);
  rect.vertex(v[1].x, v[1].y);
  // 辺bをジグザクに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 3.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 3.0/4.0, -1.0/3.0);
  rect.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  rect.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  rect.vertex(v[2].x, v[2].y); 
  // 辺cは変形できず、直線のみ。
  rect.vertex(v[3].x, v[3].y);
  // 辺dを辺bと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[3], 3.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[3], 3.0/4.0, -1.0/3.0);
  rect.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  rect.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  rect.vertex(v[0].x, v[0].y);

  rect.endShape();
  
  return rect;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

PG群の基本図形の変形

PG群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

PG群の基本図形に対する辺のラベルと向き

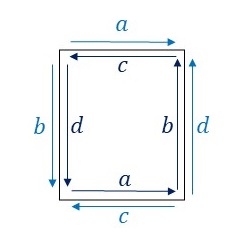
辺\(a\)と辺\(c\)は異なる向きに重なっています。つまり、辺\(a\)を適当に変形したあと、辺\(c\)は、変形した辺\(a\)を上下左右反転した形状に変形します。一方、辺\(b\)と辺\(d\)は同じ向きに重なっています。つまり、辺\(b\)を適当に変形したあと、辺\(d\)は、変形した辺\(b\)を上下反転した形状に変形します。そうすると、隣り合う基本図形同士を重ねることなくPG群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってPG群の基本図形を下図のように変形してみました。

PG群の基本図形の変形

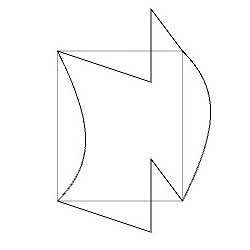
この変形した基本図形をPG群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

ＰG群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（PG）」に記載しているプログラムコードのうち、makeRecurRectangle関数を下記のtransformRectangle関数に置き換えたものになります。

// 長方形を変形する関数（基本図形）
PShape transformRectangle(){
  
  PVector[] v = new PVector[4]; // 長方形の頂点
  PShape rect = createShape();

  rect.beginShape(); // 4点ずつの頂点から長方形を作る
  v[0] = base[0].copy();
  v[0].sub(base[1]);
  v[0].mult(-scalar / 2.0);
  v[1] = base[0].copy();
  v[1].add(base[1]);
  v[1].mult(scalar / 2.0);
  v[2] = base[0].copy();
  v[2].sub(base[1]);
  v[2].mult(scalar / 2.0);
  v[3] = base[0].copy();
  v[3].add(base[1]);
  v[3].mult(-scalar / 2.0);

  // 長方形を変形する
  rect.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  // 辺aをジグザグに変形する
  rect.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, -1.0/3.0);
  rect.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  rect.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  rect.vertex(v[1].x, v[1].y); 
  // 辺bをベジエ曲線で変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 1.0/2.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 3.0/4.0, 1.0/4.0);
  rect.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[2].x, v[2].y);
  // 辺cを辺aを上下左右に反転させた形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 1.0/4.0, -1.0/4.0);
  rect.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  rect.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  rect.vertex(v[3].x, v[3].y); 
  // 辺dを辺bを上下に反転させた形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[3], v[0], 1.0/2.0, -1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[3], v[0], 3.0/4.0, -1.0/4.0);
  rect.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[0].x, v[0].y);

  rect.endShape();
  
  return rect;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

PMM群の基本図形の変形

PMM群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

PMM群の基本図形に対する辺のラベルと向き

辺\(a,b,c,d\)すべてについてそれぞれ両側のラベルが同じで向きも同じになっていますので、全ての辺を変形できず、線分となります。つまり、長方形から形を変えることができません。PMM群については以下省略します。

PMG群の基本図形の変形

PMG群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

PMG群の基本図形に対する辺のラベルと向き

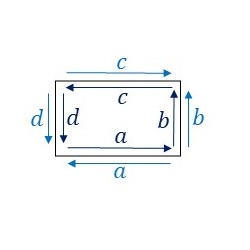
辺\(a\)と辺\(c\)についてはそれぞれ両側のラベルが同じで向きが異なっていますので、中点に関して点対称な変形を行います。辺\(b\)と辺\(d\)についてはそれぞれ両側のラベルが同じで向きも同じになっていますので、変形できず、線分となります。そうすると、隣り合う基本図形同士を重ねることなくPMG群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってPMG群の基本図形を下図のように変形してみました。

PMG群の基本図形の変形

この変形した基本図形をPMG群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

ＰMG群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（PMG）」に記載しているプログラムコードのうち、makeRecurRectangle関数を下記のtransformRectangle関数に置き換えたものになります。

// 長方形を変形する関数（基本図形）
PShape transformRectangle(){
  
  PVector[] v = new PVector[4]; // 長方形の頂点
  PShape rect = createShape();

  v[0] = base[0].copy();
  v[0].sub(base[1]);
  v[0].mult(-scalar / 2.0);
  v[1] = base[0].copy();
  v[1].add(base[1]);
  v[1].mult(scalar / 2.0);
  v[2] = base[0].copy();
  v[2].mult(scalar / 2.0);  
  v[3] = base[0].copy();
  v[3].mult(-scalar / 2.0);

  // 長方形を変形する
  rect.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  // 辺aをベジエ曲線で中点で対称になるように変形する
  rect.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 1.0/2.0, 1.0/3.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 1.0/2.0, -1.0/3.0); 
  rect.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[1].x, v[1].y);
  // 辺bは変形できず、直線のみ。
  rect.vertex(v[2].x, v[2].y);
  // 辺cをジグザグに中点で対称になるように変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 1.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 3.0/4.0, -1.0/4.0);
  rect.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  rect.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  rect.vertex(v[3].x, v[3].y); 
  // 辺dは変形できず、直線のみ。
  rect.vertex(v[0].x, v[0].y);

  rect.endShape();
  
  return rect;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

PGG群の基本図形の変形

PGG群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

PGG群の基本図形に対する辺のラベルと向き

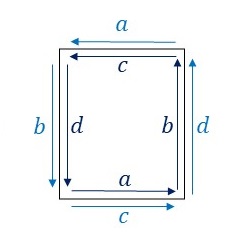
辺\(a\)と辺\(c\)、および辺\(b\)と辺\(d\)はそれぞれ同じ向きに重なっています。つまり、辺\(a\)を適当に変形したあと、辺\(c\)は、変形した辺\(a\)を上下反転した形状に変形します。辺\(b\)と辺\(d\)にも同様の変形を行います。そうすると、隣り合う基本図形同士を重ねることなくPGG群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってPGG群の基本図形を下図のように変形してみました。

PGG群の基本図形の変形

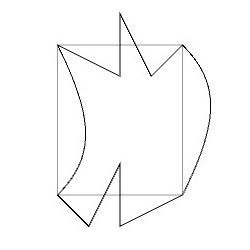
この変形した基本図形をPGG群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

PGG群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（PGG）」に記載しているプログラムコードのうち、makeRecurRectangle関数を下記のtransformRectangle関数に置き換えたものになります。

// 長方形を変形する関数（基本図形）
PShape transformRectangle(){
  
  PVector[] v = new PVector[4]; // 長方形の頂点
  PShape rect = createShape();

  v[0] = base[0].copy();
  v[0].sub(base[1]);
  v[0].mult(-scalar / 2.0);
  v[1] = base[0].copy();
  v[1].add(base[1]);  
  v[1].mult(scalar / 2.0);
  v[2] = base[0].copy();
  v[2].sub(base[1]);
  v[2].mult(scalar / 2.0);
  v[3] = base[0].copy();
  v[3].add(base[1]);
  v[3].mult(-scalar / 2.0);

  // 長方形を変形する
  rect.beginShape(); 
  PVector[] auxiliary_point = new PVector[3];
  // 辺aをジグザグに変形する
  rect.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 1.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 1.0/2.0, -1.0/4.0);
  auxiliary_point[2] = getAuxiliaryPoint(v[0], v[1], 1.0/2.0, 1.0/4.0);
  rect.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  rect.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  rect.vertex(auxiliary_point[2].x, auxiliary_point[2].y);
  rect.vertex(v[1].x, v[1].y); 
  // 辺bをベジエ曲線で変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 1.0/2.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 3.0/4.0, 1.0/4.0);
  rect.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[2].x, v[2].y);
  // 辺cを辺aを上下に反転させた形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 1.0/4.0, -1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 1.0/2.0, 1.0/4.0);
  auxiliary_point[2] = getAuxiliaryPoint(v[2], v[3], 1.0/2.0, -1.0/4.0);
  rect.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  rect.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  rect.vertex(auxiliary_point[2].x, auxiliary_point[2].y);
  rect.vertex(v[3].x, v[3].y); 
  // 辺dを辺bを上下に反転させた形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[3], v[0], 1.0/2.0, -1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[3], v[0], 3.0/4.0, -1.0/4.0);
  rect.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[0].x, v[0].y);

  rect.endShape();
  
  return rect;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

CM群の基本図形の変形

CM群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

CM群の基本図形に対する辺のラベルと向き

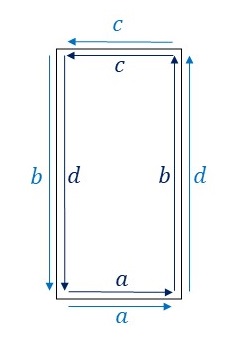
辺\(a\)と辺\(c\)についてはそれぞれ両側のラベルが同じで向きも同じになっていますので、変形できず、線分となります。辺\(b\)と辺\(d\)は同じ向きに重なっています。つまり、辺\(b\)を適当に変形したあと、辺\(d\)は、変形した辺\(b\)を上下反転した形状に変形します。そうすると、隣り合う基本図形同士を重ねることなくCM群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってCM群の基本図形を下図のように変形してみました。

CM群の基本図形の変形

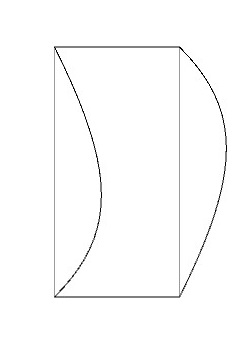
この変形した基本図形をCM群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

CM群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（CM）」に記載しているプログラムコードのうち、makeRecurRectangle関数を下記のtransformRectangle関数に置き換えたものになります。

// 長方形を変形する関数（基本図形）
PShape transformRectangle(){
  
  PVector[] v = new PVector[4]; // 長方形の頂点
  PShape rect = createShape();

  v[0] = new PVector(-base[1].x, base[1].y);
  v[0].mult(scalar);
  v[1] = base[1].copy();
  v[1].mult(scalar);
  v[2] = new PVector(base[1].x, -base[1].y);
  v[2].mult(scalar);
  v[3] = base[1].copy();
  v[3].mult(-scalar);

  // 長方形を変形する
  rect.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  // 辺aは変形できず、直線のみ。
  rect.vertex(v[0].x, v[0].y);
  rect.vertex(v[1].x, v[1].y);
  // 辺bをベジエ曲線で変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 1.0/2.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 3.0/4.0, 1.0/4.0);
  rect.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[2].x, v[2].y);
  // 辺cは変形できず、直線のみ。
  rect.vertex(v[3].x, v[3].y);
  // 辺dを辺bを上下に反転させた形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[3], v[0], 1.0/2.0, -1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[3], v[0], 3.0/4.0, -1.0/4.0);
  rect.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[0].x, v[0].y);

  rect.endShape();
  
  return rect;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

CMM群の基本図形の変形

CMM群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

CMM群の基本図形に対する辺のラベルと向き

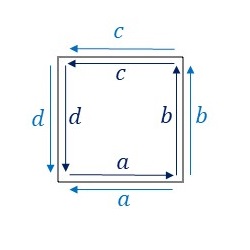
辺\(a\)については両側のラベルが同じで向きが異なっていますので、中点に関して点対称な変形を行います。残りの辺\(b, c, d\)についてはそれぞれ両側のラベルが同じで向きも同じになっていますので、変形できず、線分となります。そうすると、隣り合う基本図形同士を重ねることなくCMM群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってCMM群の基本図形を下図のように変形してみました。

CMM群の基本図形の変形

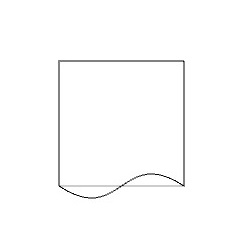
この変形した基本図形をCMM群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

CMM群の変形した基本図形による図形

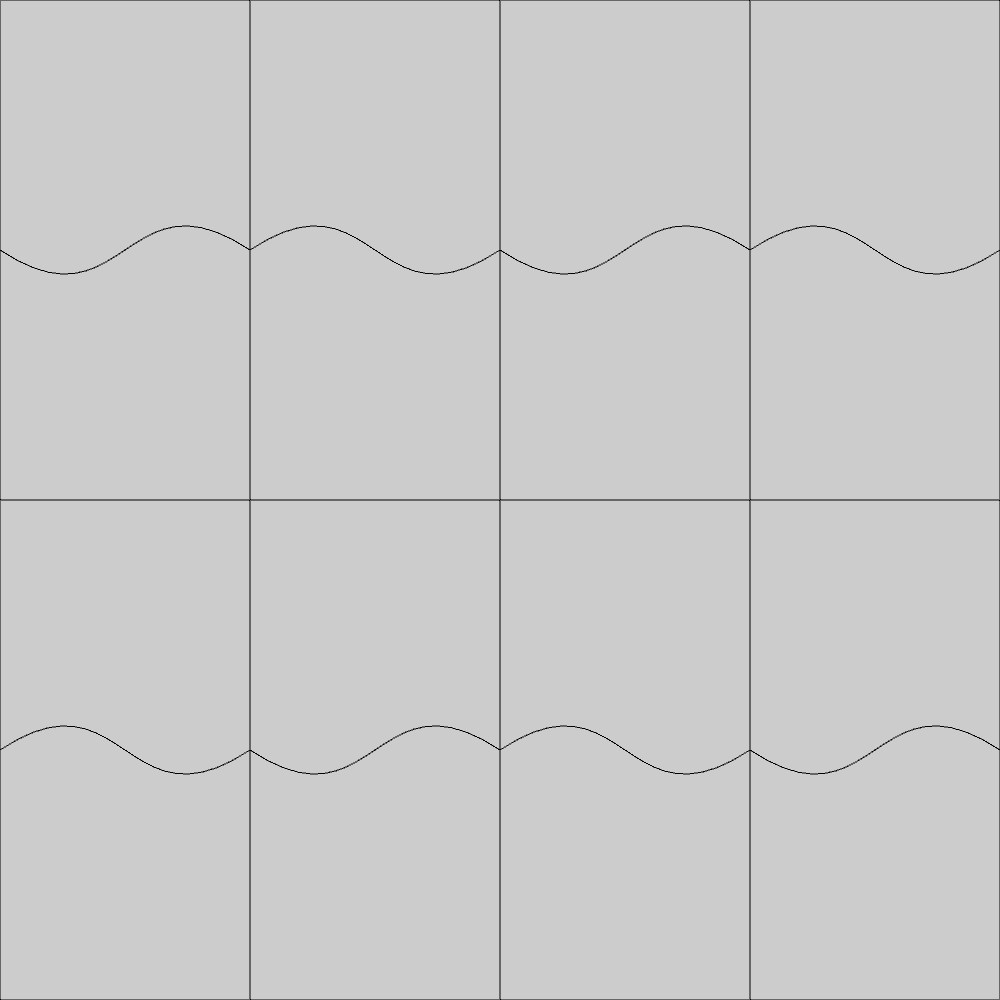
なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（CMM）」に記載しているプログラムコードのうち、makeRecurRectangle関数を下記のtransformRectangle関数に置き換えたものになります。

// 長方形を変形する関数（基本図形）
PShape transformRectangle(){
  
  PVector[] v = new PVector[4]; // 長方形の頂点
  PShape rect = createShape();

  v[0] = base[1].copy().sub(base[0].copy().mult(0.5));
  v[0].mult(scalar);
  v[1] = base[1].copy().add(base[0].copy().mult(0.5));
  v[1].mult(scalar);
  v[2] = base[0].copy();
  v[2].mult(scalar);
  v[3] = new PVector(0.0, 0.0);

  // 長方形を変形する
  rect.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  rect.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 1.0/2.0, 1.0/3.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 1.0/2.0, -1.0/3.0); 
  rect.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[1].x, v[1].y);
  // 辺cは変形できず、直線のみ。
  rect.vertex(v[2].x, v[2].y);
  // 辺cは変形できず、直線のみ。
  rect.vertex(v[3].x, v[3].y);
  // 辺cは変形できず、直線のみ。
  rect.vertex(v[0].x, v[0].y);

  rect.endShape();
  
  return rect;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

P4群の基本図形の変形

P4群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P4群の基本図形に対する辺のラベルと向き

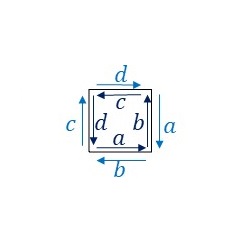
辺\(a\)と辺\(b\)、および辺\(c\)と辺\(d\)がそれぞれ異なる向きに重なっています。つまり、辺\(a\)を適当に変形したあと、辺\(b\)は、変形した辺\(a\)を上下左右反転した形状に変形します。また辺\(c\)と辺\(d\)についても同じように変形します。ただし、条件として上図正方形の左上の頂点が正方格子の点となるようにする必要があります。そうすると、隣り合う基本図形同士を重ねることなくP4群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってP4群の基本図形を下図のように変形してみました。

P4群の基本図形の変形

この変形した基本図形をP4群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

P4群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（P4）」に記載しているプログラムコードのうち、makeRecurSquare関数を下記のtransformSquare関数に置き換えたものになります。

// 正方形を変形する関数（基本図形）
PShape transformSquare(){
  
  PVector[] v = new PVector[4]; // 正方形の頂点
  PShape square = createShape();

  v[0] = base[1].copy();
  v[0].mult(scalar / 2.0);
  v[1] = base[0].copy();
  v[1].add(base[1]);
  v[1].mult(scalar / 2.0);  
  v[2] = base[0].copy();
  v[2].mult(scalar / 2.0);
  v[3] = new PVector(0.0,0.0);

  // 正方形を変形する
  square.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  // 辺aをジグザグに変形する
  square.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 1.0/4.0, 1.0/4.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 1.0/4.0, -1.0/6.0); 
  square.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  square.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  square.vertex(v[1].x, v[1].y);
  // 辺bを辺aと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[1], 1.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[1], 1.0/4.0, -1.0/6.0);
  square.vertex(auxiliary_point[1].x, auxiliary_point[1].y);  
  square.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  square.vertex(v[2].x, v[2].y);
  // 辺cをベジエ曲線で変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 3.0/4.0, 1.0/4.0); 
  square.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[3].x, v[3].y);
  // 辺dを辺cと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[3], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[3], 3.0/4.0, 1.0/4.0);
  square.bezierVertex(auxiliary_point[1].x, auxiliary_point[1].y, auxiliary_point[0].x, auxiliary_point[0].y, v[0].x, v[0].y);  

  square.endShape();
  
  return square;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

P4M群の基本図形の変形

P4M群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P4M群の基本図形に対する辺のラベルと向き

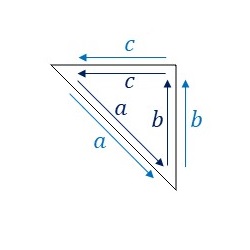
辺\(a,b,c\)すべてについてそれぞれ両側のラベルが同じで向きも同じになっていますので、全ての辺を変形できず、線分となります。つまり、直角二等辺三角形から形を変えることができません。P4M群については以下省略します。

P4G群の基本図形の変形

P4G群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P4G群の基本図形に対する辺のラベルと向き

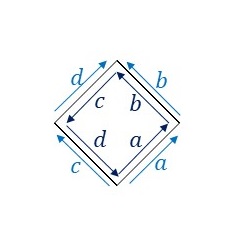
辺\(a\)と辺\(b\)についてそれぞれ両側のラベルが同じで向きも同じになっていますので、変形できず、線分となります。 辺\(c\)と辺\(d\)は異なる向きに重なっています。つまり、辺\(c\)を適当に変形したあと、辺\(d\)は、変形した辺\(c\)を上下左右反転した形状に変形します。そうすると、隣り合う基本図形同士を重ねることなくP4G群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってP4G群の基本図形を下図のように変形してみました。

P4G群の基本図形の変形

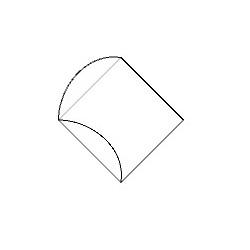
この変形した基本図形をP4G群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

P4G群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（P4G）」に記載しているプログラムコードのうち、makeRecurSquare関数を下記のtransformSquare関数に置き換えたものになります。

// 正方形を変形する関数（基本図形）
PShape transformSquare(){
  
  PVector[] v = new PVector[4]; // 正方形の頂点
  PShape square = createShape();

  v[0] = base[1].copy();
  v[0].mult(scalar / 2.0);
  v[1] = base[0].copy();
  v[1].mult(scalar / 2.0);
  v[2] = base[1].copy();
  v[2].mult(-scalar / 2.0);
  v[3] = base[0].copy();
  v[3].mult(-scalar / 2.0);

  // 正方形を変形する
  square.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  // 辺aは変形できず、直線のみ。
  square.vertex(v[0].x, v[0].y);
  square.vertex(v[1].x, v[1].y);
  // 辺bは変形できず、直線のみ。
  square.vertex(v[2].x, v[2].y);
  // 辺cをベジエ曲線で変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 3.0/4.0, 1.0/4.0); 
  square.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[3].x, v[3].y);
  // 辺dを辺cと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[3], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[3], 3.0/4.0, 1.0/4.0);
  square.bezierVertex(auxiliary_point[1].x, auxiliary_point[1].y, auxiliary_point[0].x, auxiliary_point[0].y, v[0].x, v[0].y);  

  square.endShape();
  
  return square;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

P3群の基本図形の変形

P3群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P3群の基本図形に対する辺のラベルと向き

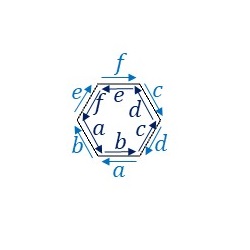
辺\(a\)と辺\(b\)、辺\(c\)と辺\(d\)、および辺\(e\)と辺\(f\)がそれぞれ異なる向きに重なっています。つまり、辺\(a\)を適当に変形したあと、辺\(b\)は、変形した辺\(a\)を上下左右反転した形状に変形します。また辺\(c\)と辺\(d\)、辺\(e\)と辺\(f\)についても同じように変形します。そうすると、隣り合う基本図形同士を重ねることなくP3群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってP3群の基本図形を下図のように変形してみました。

P3群の基本図形の変形

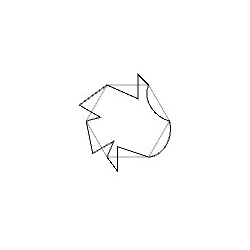
この変形した基本図形をP3群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

P3群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（P3）」に記載しているプログラムコードのうち、makeRecurHexagon関数を下記のtransformHexagon関数に置き換えたものになります。

// 正六角形を変形する関数（基本図形）
PShape transformHexagon(){
  
  PVector[] v = new PVector[6]; // 正六角形の頂点
  PShape hexagon = createShape();
  
  for (int i=0; i<6; i++){
    v[i] = PVector.fromAngle(-i * PI / 3 + PI).mult(scalar / 3.0);
    v[i].add( base[1].copy().mult(scalar / 3.0) );
  }

  hexagon.beginShape(); // 6点ずつの頂点から正六角形の頂点を作る
  PVector[] auxiliary_point = new PVector[2];
  // 辺aをジグザグに変形する
  hexagon.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, 1.0/4.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, -1.0/3.0); 
  hexagon.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  hexagon.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  hexagon.vertex(v[1].x, v[1].y);
  // 辺bを辺aと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[1], 3.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[1], 3.0/4.0, -1.0/3.0);
  hexagon.vertex(auxiliary_point[1].x, auxiliary_point[1].y);  
  hexagon.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  hexagon.vertex(v[2].x, v[2].y);
  // 辺cをベジエ曲線で変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 3.0/4.0, 1.0/4.0); 
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[3].x, v[3].y);
  // 辺dを辺cと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[4], v[3], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[4], v[3], 3.0/4.0, 1.0/4.0);
  hexagon.bezierVertex(auxiliary_point[1].x, auxiliary_point[1].y, auxiliary_point[0].x, auxiliary_point[0].y, v[4].x, v[4].y);  
  // 辺eをジグザグに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[4], v[5], 1.0/4.0, 1.0/4.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[4], v[5], 1.0/4.0, -1.0/3.0); 
  hexagon.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  hexagon.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  hexagon.vertex(v[5].x, v[5].y);
  // 辺fを辺eと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[5], 1.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[5], 1.0/4.0, -1.0/3.0);
  hexagon.vertex(auxiliary_point[1].x, auxiliary_point[1].y);  
  hexagon.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  hexagon.vertex(v[0].x, v[0].y);

  hexagon.endShape();
  
  return hexagon;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

P3M1群の基本図形の変形

P3M1群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P3M1群の基本図形に対する辺のラベルと向き

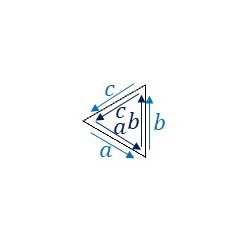
辺\(a,b,c\)すべてについてそれぞれ両側のラベルが同じで向きも同じになっていますので、全ての辺を変形できず、線分となります。つまり、正三角形から形を変えることができません。P3M1群については以下省略します。

P31M群の基本図形の変形

P31M群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P31M群の基本図形に対する辺のラベルと向き

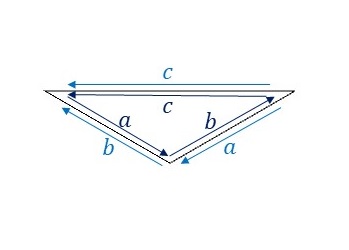
辺\(a\)と辺\(b\)が異なる向きに重なっています。つまり、辺\(a\)を適当に変形したあと、辺\(b\)は、変形した辺\(a\)を上下左右反転した形状に変形します。辺\(c\)は両側のラベルが同じで向きも同じになっていますので、変形できず、線分となります。そうすると、隣り合う基本図形同士を重ねることなくP31M群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってP31M群の基本図形を下図のように変形してみました。

P31M群の基本図形の変形

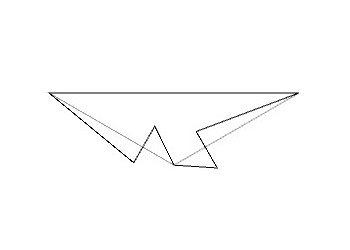
この変形した基本図形をP31M群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

P31M群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（P31M）」に記載しているプログラムコードのうち、makeRecurTriangle関数を下記のtransformTriangle関数に置き換えたものになります。

// 二等辺三角形を変形する関数（基本図形）
PShape transformTriangle(){

  PVector[] v = new PVector[3]; // 二等辺三角形の頂点
  PShape tri = createShape();
  
  v[2] = new PVector(0,0);
  v[0] = PVector.fromAngle(0.0);
  v[0].mult(2.0 * scalar);
  v[1] = PVector.fromAngle(PI / 6);
  v[1].mult(2.0 * scalar / sqrt(3));

  // 二等辺三角形を変形する
  tri.beginShape();
  PVector[] auxiliary_point = new PVector[2];
  // 辺aをジグザグに変形する
  tri.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, 1.0/8.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, -1.0/6.0); 
  tri.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  tri.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  tri.vertex(v[1].x, v[1].y);
  // 辺bを辺aと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[1], 3.0/4.0, 1.0/8.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[1], 3.0/4.0, -1.0/6.0);
  tri.vertex(auxiliary_point[1].x, auxiliary_point[1].y);  
  tri.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  tri.vertex(v[2].x, v[2].y);
  // 辺cは変形できず、直線のみ。
  tri.vertex(v[0].x, v[0].y);
  
  tri.endShape(CLOSE);
  
  return tri;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

P6群の基本図形の変形

P6群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P6群の基本図形に対する辺のラベルと向き

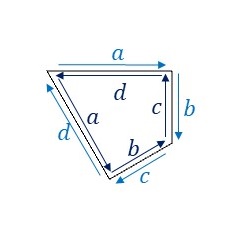
辺\(a\)と辺\(d\)、および辺\(b\)と辺\(c\)がそれぞれ異なる向きに重なっています。つまり、辺\(a\)を適当に変形したあと、辺\(d\)は、変形した辺\(a\)を上下左右反転した形状に変形します。また辺\(b\)と辺\(c\)についても同じように変形します。そうすると、隣り合う基本図形同士を重ねることなくP6群の対称性に従って敷き詰めることができます。ここでは、このルールに従ってP6群の基本図形を下図のように変形してみました。

P6群の基本図形の変形

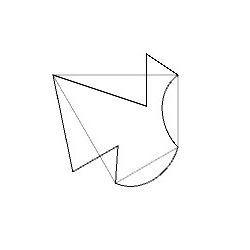
この変形した基本図形をP6群の対称性を考慮して並べていくと、下図のような図形を得ることができます。

P6群の変形した基本図形による図形

なお、この図形を作成するためのプログラムコードは、別記事「渦巻き図形（P6）」に記載しているプログラムコードのうち、makeRecurKite関数を下記のtransformKite関数に置き換えたものになります。

// 凧型を変形する関数（基本図形）
PShape transformKite(){

  PVector[] v = new PVector[4]; // 凧型の頂点
  PShape kite = createShape();

  v[0] = new PVector(0,0);
  v[1] = PVector.fromAngle(PI / 3);
  v[1].mult(scalar);
  v[2] = PVector.fromAngle(PI / 6);
  v[2].mult(2.0 * scalar / sqrt(3));
  v[3] = new PVector(1.0,0.0);
  v[3].mult(scalar);

  // 凧型を変形する
  kite.beginShape(); 
  PVector[] auxiliary_point = new PVector[2];
  // 辺aをジグザグに変形する
  kite.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, 1.0/4.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 3.0/4.0, -1.0/6.0); 
  kite.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  kite.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
  kite.vertex(v[1].x, v[1].y);
  // 辺bをベジエ曲線で変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 3.0/4.0, 1.0/4.0); 
  kite.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[2].x, v[2].y);
  // 辺cを辺bと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[3], v[2], 1.0/4.0, 1.0/3.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[3], v[2], 3.0/4.0, 1.0/4.0);
  kite.bezierVertex(auxiliary_point[1].x, auxiliary_point[1].y, auxiliary_point[0].x, auxiliary_point[0].y, v[3].x, v[3].y);  
  // 辺dを辺aと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[3], 3.0/4.0, 1.0/4.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[3], 3.0/4.0, -1.0/6.0);
  kite.vertex(auxiliary_point[1].x, auxiliary_point[1].y);  
  kite.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
  kite.vertex(v[0].x, v[0].y);
  kite.endShape();
  
  return kite;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

P6M群の基本図形の変形

P6M群の基本図形について、隣り合う基本図形同士の辺のラベルと向きをみてみます。

P6M群の基本図形に対する辺のラベルと向き

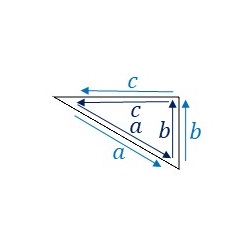
辺\(a,b,c\)すべてについてそれぞれ両側のラベルが同じで向きも同じになっていますので、全ての辺を変形できず、線分となります。つまり、直角三角形から形を変えることができません。P6M群については以下省略します。

コメントを残す