渦巻き図形（P6M）

  1. ホーム
  2. 壁紙アート
  3. 渦巻き図形
  4. 渦巻き図形（P6M）

ここでは、P6Mのパターンで渦巻き図形による壁紙アートを作成しています。結果は以下のようになりました。

渦巻き図形による壁紙アート（P6M）

この壁紙アートにおける基本図形とタイルは以下のようなものです。タイルは基本図形と基本図形を反転させたものを組み合わせて正三角形を作り、その正三角形を順に60°回転させたものを組み合わせて作成しています。

P6Mの基本図形（左）とタイル（右）

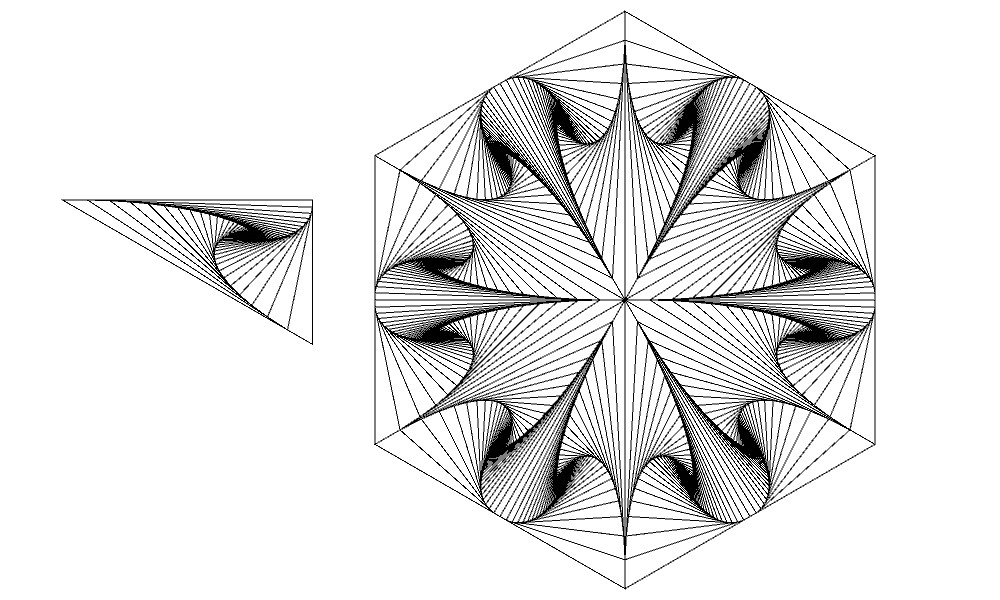
以下、この図形を描画するためのプログラムソースコードを載せておきます（Processingで動きます）。

PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
PVector[] base = new PVector[2]; // 格子を張るベクトル
int col_num = 4; // 描画するタイルの列の数
float scalar; // タイルの辺の長さ

void setup(){

  size(1000, 1000, P2D);
  scalar = width * 1.0 / col_num; // 描画ウィンドウと行の数からタイルの大きさを決定
  makeTriangleVector(); // 三角格子を張るベクトルの生成
  makeLattice(); // 格子点ベクトルを生成
  makeTileP6M(); // タイルを生成
  drawTiling(); // タイリングを描画
  
  save("P6M_spiral.jpg");
}

// 三角格子を張るベクトルを生成する関数
void makeTriangleVector(){
  base[0] = new PVector(1.0, 0.0);
  base[1] = PVector.fromAngle(PI / 3);
}

// 三角格子を生成する関数
void makeLattice(){
  int row_num = ceil(col_num / base[1].x); // 行の数
  lattice = new PVector[col_num + 3][row_num + 1];
  for (int i = 0; i < col_num + 3; i++){
    for (int j = 0; j < row_num + 1; j++){
      PVector v = PVector.mult(base[0], i * scalar); 
      v.add(PVector.mult(base[1], j * scalar));
      lattice[i][j] = new PVector(v.x % ((col_num+3)*scalar) - 2 * scalar, v.y); // x軸方向にscalarの2倍だけ左にシフト
    }
  }
}

// 再帰的な直角三角形を生成する関数（基本図形）
PShape makeRecurRightTriangle(){
  float gap = 0.1; // 再帰的な直角三角形を作るパラメータ
  PVector[] v = new PVector[3]; // 直角三角形の頂点

  PShape rightTri = createShape();
  v[2] = new PVector(0,0);
  v[0] = new PVector(1.0,0.0);
  v[0].mult(scalar);
  v[1] = PVector.fromAngle(PI / 6);
  v[1].mult(2.0 * scalar / sqrt(3));

  rightTri.beginShape(TRIANGLES); // 3点ずつの頂点から直角三角形を作る
  while( v[0].dist(v[1]) > 1){
    for (int i=0; i<3; i++){
      rightTri.vertex(v[i].x, v[i].y);
    }
    v = getVector(v, gap); // gapの分だけずらした直角三角形の頂点を取得
  }
  
  rightTri.endShape();
    
  return rightTri;
}

PVector[] getVector(PVector[] v, float gap){
  PVector[] nextVec = new PVector[3];
  for (int i=0; i<3; i++){
    PVector dir = PVector.sub(v[(i+1)%3], v[i]);
    if(i == 0){
      dir.mult(gap/2.0); // 図形の形状を少しずつ変形していく
    } else {
      dir.mult(gap);
    }
    nextVec[i] = PVector.add(v[i], dir);
  }
  return nextVec;
}

// タイルを生成する関数
void makeTileP6M(){
  tile = createShape(GROUP); // PShapeのグループを作る
  for (int i=0; i<6; i++){
    PShape positiveTri = createShape(GROUP); // 直角三角形を2つ合わせて正三角形を生成
    for (int j=0; j<2; j++){
      PShape rightTri = makeRecurRightTriangle(); // 再帰的な直角三角形の生成
      rightTri.scale(1, pow(-1, j)); // x軸を中心に鏡映
      positiveTri.addChild(rightTri);
    }
    positiveTri.rotate(PI * i / 3.0); // 60度回転
    tile.addChild(positiveTri); // グループに追加
  }
}

// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
  background(255);
  for (int i=0; i<lattice.length; i++){
    for (int j=0; j<lattice[0].length; j++){
      if( i%2 == 0 && j%2 == 0 ){
        tile.resetMatrix();
        tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
        shape(tile); // タイルを描画
      }
    }
  }
  // 格子点を描く
  for (int i=0; i<lattice.length; i++){
    for (int j=0; j<lattice[0].length; j++){
      circle(lattice[i][j].x, lattice[i][j].y, 10);
    }
  }
}

コメントを残す