ここでは、正三角形と正方形によるタイリング(2通りあるうちの1つで「正三角形と正方形②」とします)を再現してみました。なお、今回のタイリングを作成するにあたって、書籍「アートで魅せる数学の世界」の「2種類以上の正多角形によるタイリング」(p.94)を参考にしました。
Contents
正三角形と正方形②
タイリング〈正三角形と正方形②〉は以下のような図形になります。

以下で、このタイリング〈正三角形と正方形②〉の描き方について解説していきます。
正三角形と正方形②の描き方
対称性について
まず、このタイリング〈正三角形と正方形②〉の対称性について考えます。

上図のように、タイリングのパターンをじっくり見ていくと、上図の赤丸の周りの180°回転、および赤四角の周りの90°回転に対して図形は回転対称になっていることが分かります。そして縦横の赤色の線に対して図形は鏡映対称であり、赤色の点線の軸に対して図形はすべり鏡映対称であることがわかります。また、黒色の点を格子としてみると、近接する4つの黒色の点同士が正方形を形作っていることから、黒色の点は正方格子になっていることが分かります。これらをまとめると、タイリング〈正三角形と正方形②〉は、壁紙群P4Gの対称性を持つことが分かります。
アイソヘドラルタイリングの観点でみると、IH56(P4G)、IH63(P4G)のいずれにも分類することができますが、今回は基本図形が一番細かくなるIH56(P4G)で再現しました。なお、以下では、IH56(P4G)の拡張版の方がわかりやすいと思いますので、そちらで解説しています。
基本図形の準備
タイリング〈正三角形と正方形②〉に現れる正三角形や正方形の一辺の長さを\(1\)とすると、タイリング〈正三角形と正方形②〉の基本図形は、斜辺の長さが\(1\)となる直角二等辺三角形と、斜辺の長さが\(1\)となる30°、60°、90°の直角三角形を組み合わせたものになります(下図参照)。
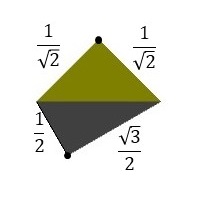
正方格子の準備
また、正方格子は、上図の基本図形で示したように、直角二等辺三角形の直角となる頂点と、30°、60°、90°の直角三角形の直角となる頂点が近接する正方格子点となるように準備します。
壁紙群P4Gの対称性に合わせて並べる
ここまで準備ができたら、あとは壁紙群P4Gの対称性に合わせて基本図形を並べていくことでタイリング〈正三角形と正方形②〉を作成することができます。
ソースコード
今回再現したタイリング〈正三角形と正方形②〉のプログラムのソースコードを示しておきます。
PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
PVector[] base = new PVector[2]; // 格子を張るベクトル
int col_num = 8; // 描画するタイルの列の数
float scalar; // タイルの辺の長さ
void setup(){
size(1000, 1000, P2D);
noFill();
noLoop();
scalar = width * 1.0 / col_num; // 描画ウィンドウと行の数からタイルの大きさを決定
makeSquareVector(); // 正方格子を張るベクトルの生成
makeLattice(); // 格子点ベクトルを生成
makeTileP4G(); // タイルを生成
drawTiling(); // タイリングを描画
}
// 正方格子を張るベクトルを生成する関数
void makeSquareVector(){
PVector[] v = new PVector[4]; // 四角形の頂点
v[3] = new PVector(0.0,0.0);
v[1] = new PVector(1.0,0.0).mult(scalar);
v[0] = PVector.fromAngle( radians(60.0) ).mult( scalar / 2.0);
v[2] = PVector.fromAngle( -radians(45.0) ).mult( scalar / sqrt(2.0));
base[1] = v[0].copy().sub(v[2].copy());
base[0] = base[1].copy().rotate( -radians(90.0) );
}
// 正方格子を生成する関数
void makeLattice(){
int row_num = ceil(height / base[1].y); // 行の数
lattice = new PVector[col_num + 5][row_num + 5];
for (int i = 0; i < col_num + 5; i++){
for (int j = 0; j < row_num + 5; j++){
PVector v = PVector.mult(base[0], i-2);
v.add(PVector.mult(base[1], j-2));
lattice[i][j] = new PVector(v.x, v.y);
}
}
}
// 四角形を生成する関数(基本図形)
PShape makeRectangle(){
PVector[] v = new PVector[4]; // 四角形の頂点
v[3] = new PVector(0.0,0.0);
v[1] = new PVector(1.0,0.0).mult(scalar);
v[0] = PVector.fromAngle( radians(60.0) ).mult( scalar / 2.0);
v[2] = PVector.fromAngle( -radians(45.0) ).mult( scalar / sqrt(2.0));
PVector dir = v[2].copy();
for(int i=0; i<4; i++){
v[i].sub(dir.copy());
}
PShape rect = createShape(GROUP);
// 直角二等辺三角形を描く
fill(128,128,0);
noStroke();
PShape tri1 = createShape();
tri1.beginShape();
tri1.vertex(v[1].x, v[1].y);
tri1.vertex(v[2].x, v[2].y);
tri1.vertex(v[3].x, v[3].y);
tri1.endShape(CLOSE);
rect.addChild(tri1);
// 30,60,90の直角三角形を描く
fill(64,64,64);
noStroke();
PShape tri2 = createShape();
tri2.beginShape();
tri2.vertex(v[0].x, v[0].y);
tri2.vertex(v[1].x, v[1].y);
tri2.vertex(v[3].x, v[3].y);
tri2.endShape(CLOSE);
rect.addChild(tri2);
// 三角形の一部の輪郭を描く
stroke(0,0,0);
PShape tri2_line = createShape();
tri2_line.beginShape();
tri2_line.vertex(v[0].x, v[0].y);
tri2_line.vertex(v[3].x, v[3].y);
tri2_line.vertex(v[0].x, v[0].y);
tri2_line.endShape(CLOSE);
rect.addChild(tri2_line);
return rect;
}
// タイルを生成する関数
void makeTileP4G(){
float angle = PVector.angleBetween( base[0], new PVector(1.0,0.0) );
tile = createShape(GROUP); // PShapeのグループを作る
for(int j=0; j<2; j++){
for(int i=0; i<4; i++){
PShape square = makeRectangle(); // 変形した四角形の生成
square.scale(pow(-1,j),1); // 四角形の反転
square.rotate(i*radians(90) + 2.0 * angle * j); // 四角形の回転
square.translate(j*( base[0].x + base[1].x ), j*( base[0].y + base[1].y )); // 四角形の位置を調整
tile.addChild(square); // グループに追加
}
}
}
// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
// background(255);
for (int i=0; i<lattice.length; i++){
for (int j=0; j<lattice[0].length; j++){
if( i%2 == 0 && j%2==0 ){
tile.resetMatrix();
tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
shape(tile); // タイルを描画
}
}
}
}参考
参考までに、アイソヘドラルタイリングIH63(P4G)とみなしたときの基本図形を示しておきます。
