ここでは、書籍「アートで魅せる数学の世界」のp.105-109で解説されているフォーデルベルク・タイリングについて再現を試みています。
Contents
フォーデルベルク・タイリング
今回再現したフォーデルベルク・タイリングを示します。
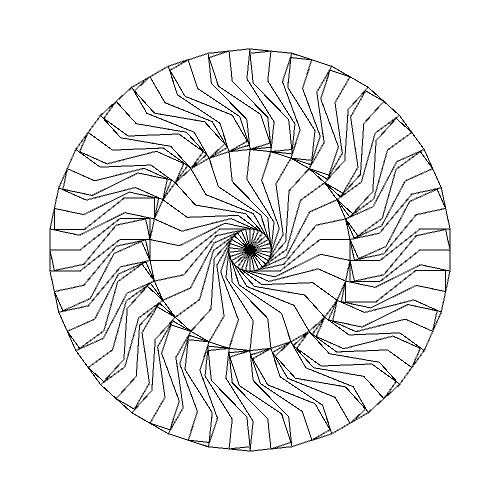

フォーデルベルク・タイリングは非周期タイリングの一つで、以下の九角形の基本図形をうまく組み合わせて並べていくことで実現できます。
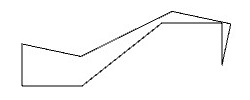
この九角形の基本図形の作り方は書籍「アートで魅せる数学の世界」のp.107-108で丁寧に解説されていますので、ここでは省略します。
ソースコード
フォーデルベルク・タイリングのプログラムのソースコードを示しておきます。なお、最初のsetup関数内で「drawVoderbergTiling1()」を指定すると上記左側のフォーデルベルク・タイリングが描画され、「drawVoderbergTiling2()」を指定すると右側のフォーデルベルク・タイリングが描画されます。
float nonagon_size = 100.0; // 九角形の基準サイズ
void setup(){
size(500, 500, P2D);
noFill();
noLoop();
background(255,255,255);
translate(width/2.0, height/2.0);
drawVoderbergTiling1();
// drawVoderbergTiling2();
}
// 九角形(nonagon)の頂点を取得する関数
PVector[] getNonagon(){
// 基本図形の標準的な高さ
float fundamental_height = nonagon_size * tan(radians(6.0));
PVector[] v = new PVector[9];
v[0] = new PVector(0.0, 0.0);
v[4] = new PVector(-nonagon_size, -fundamental_height);
v[5] = new PVector(-nonagon_size, fundamental_height);
float theta = radians(35.0);
v[6] = new PVector( - nonagon_size + 2.0 * fundamental_height / tan(theta), fundamental_height);
v[7] = new PVector( -2.0 * fundamental_height / tan(theta), -2.0 * fundamental_height);
v[8] = new PVector( 0.0, -2.0 * fundamental_height);
v[1] = v[8].copy().rotate( radians(12.0) );
v[2] = v[7].copy().rotate( radians(12.0) );
v[3] = v[6].copy().rotate( radians(12.0) );
return v;
}
// 九角形を図形の中心周りで180°回転する関数
PVector[] getRotation180(
PVector[] v // 回転する元の図形の頂点座標
){
PVector[] rot = new PVector[9];
float angle = 180.0; // 回転角度
PVector dir = v[6].copy().add( v[7].copy().sub(v[6].copy()).mult(0.5) );
for(int i=0; i<9; i++){
PVector temp = v[i].copy().sub(dir.copy());
PVector p = temp.copy().rotate(radians(angle));
rot[i] = dir.copy().add(p.copy());
}
return rot;
}
// フォーデルベルク・タイリング1を生成する関数
void drawVoderbergTiling1(){
PVector[] v_base = getNonagon();
PVector[] v_base_rot = getRotation180(v_base);
// 基本となる図形を準備
PShape fundamental1 = createShape(GROUP);
PShape nonagon = createShape();
nonagon.beginShape();
for(int j=0; j<9; j++){
nonagon.vertex(v_base[j].x, v_base[j].y);
}
nonagon.endShape(CLOSE);
fundamental1.addChild(nonagon);
PVector[] v = new PVector[9];
PVector dir = v_base[5].copy();
PShape nonagon2 = createShape();
nonagon2.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base[j].copy().rotate(-radians(12.0)).add(dir);
nonagon2.vertex(v[j].x, v[j].y);
}
nonagon2.endShape(CLOSE);
fundamental1.addChild(nonagon2);
PShape nonagon3 = createShape();
nonagon3.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base[j].copy().rotate(-radians(12.0)*2.0).add(dir);
nonagon3.vertex(v[j].x, v[j].y);
}
nonagon3.endShape(CLOSE);
fundamental1.addChild(nonagon3);
PShape nonagon4 = createShape();
nonagon4.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base_rot[j].copy().rotate(-radians(12.0)*2.0).add(dir);
nonagon4.vertex(v[j].x, v[j].y);
}
nonagon4.endShape(CLOSE);
fundamental1.addChild(nonagon4);
// 基本図形を回転させながら30個描く
for(int i=0; i<30; i++){
fundamental1.rotate(radians(12.0));
shape(fundamental1);
}
}
// フォーデルベルク・タイリング2を生成する関数
void drawVoderbergTiling2(){
PVector[] v_base = getNonagon();
PVector[] v_base_rot = getRotation180(v_base);
PVector[] v = new PVector[9];
PShape nonagon, nonagon_rot;
PVector dir = v_base[6].copy().add( v_base[7].copy().sub(v_base[6].copy()).mult(0.5) ).mult(-1.0);
color[] colors = new color[2];
colors[0] = color(255,0,0); // 赤色
colors[1] = color(0,0,0); // 黒色
noStroke();
// 基本図形を回転させながら15個描く
for(int i=0; i<15; i++){
fill(colors[i%2]);
nonagon = createShape();
nonagon.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base[j].copy().rotate(i*radians(12.0)).add(dir);
nonagon.vertex(v[j].x, v[j].y);
}
nonagon.endShape(CLOSE);
shape(nonagon);
}
// 3つの基本図形を組み合わせたものをシフト、回転させながら15個描く
for(int i=0; i<15; i++){
fill(colors[(i+1)%2]);
nonagon = createShape();
nonagon.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base[j].copy().rotate((15+i)*radians(12.0)).add(dir);
nonagon.vertex(v[j].x, v[j].y);
}
nonagon.endShape(CLOSE);
shape(nonagon);
dir = v[1].copy();
fill(colors[i%2]);
nonagon_rot = createShape();
nonagon_rot.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base_rot[j].copy().rotate((15+i)*radians(12.0)).add(dir);
nonagon_rot.vertex(v[j].x, v[j].y);
}
nonagon_rot.endShape(CLOSE);
shape(nonagon_rot);
fill(colors[(i+1)%2]);
nonagon = createShape();
nonagon.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base[j].copy().rotate((15+i)*radians(12.0)).add(dir);
nonagon.vertex(v[j].x, v[j].y);
}
nonagon.endShape(CLOSE);
shape(nonagon);
}
// もう一つの螺旋を描いていく
dir = v_base[6].copy().add( v_base[7].copy().sub(v_base[6].copy()).mult(0.5) );
colors[0] = color(0,0,0); // 黒色
colors[1] = color(0,0,255); // 青色
// 基本図形を回転させながら15個描く
for(int i=0; i<15; i++){
fill(colors[i%2]);
nonagon = createShape();
nonagon.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base[j].copy().rotate((15+i)*radians(12.0)).add(dir);
nonagon.vertex(v[j].x, v[j].y);
}
nonagon.endShape(CLOSE);
shape(nonagon);
}
// 3つの基本図形を組み合わせたものをシフト、回転させながら15個描く
for(int i=0; i<15; i++){
fill(colors[(i+1)%2]);
nonagon = createShape();
nonagon.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base[j].copy().rotate((30+i)*radians(12.0)).add(dir);
nonagon.vertex(v[j].x, v[j].y);
}
nonagon.endShape(CLOSE);
shape(nonagon);
dir = v[1].copy();
fill(colors[i%2]);
nonagon_rot = createShape();
nonagon_rot.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base_rot[j].copy().rotate(i*radians(12.0)).add(dir);
nonagon_rot.vertex(v[j].x, v[j].y);
}
nonagon_rot.endShape(CLOSE);
shape(nonagon_rot);
fill(colors[(i+1)%2]);
nonagon = createShape();
nonagon.beginShape();
for(int j=0; j<9; j++){
v[j] = v_base[j].copy().rotate(i*radians(12.0)).add(dir);
nonagon.vertex(v[j].x, v[j].y);
}
nonagon.endShape(CLOSE);
shape(nonagon);
}
}