IH16（P31M）

  1. ホーム
  2. 壁紙アート
  3. アイソヘドラルタイリング
  4. IH16（P31M）

ここでは、アイソヘドラルタイリングIH16（P31M）について、解説します。

IH16（P31M）

アイソヘドラルタイリングIH16（P31M）の基本図形は以下のような形になります。

IH16（P31M）の基本図形

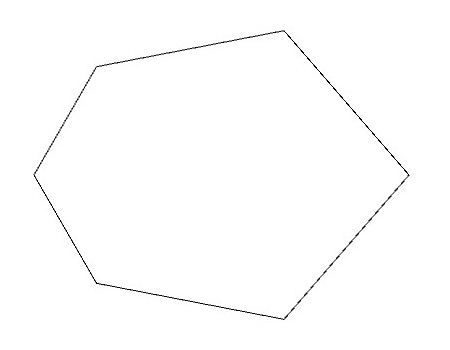
これは、記事「基本図形の形を考える」で示したP31M群の基本図形の各辺の長さを調整したものを2つ組み合わせたものになっています。

IH16（P31M）の基本図形のサイズ

この基本図形の各辺に以下の図のように、ラベルを振ります。

IH16（P31M）の基本図形のサイズ

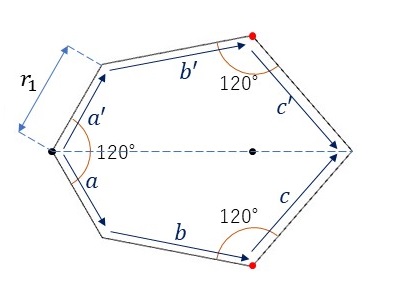
IH16（P31M）の基本図形は六角形で、上図のように点線で2つの四角形に分けると、各四角形は記事「基本図形の形を考える」で示したP31M群の基本図形の各辺の長さを調整したものであり、2つの四角形は点線でお互いに線対称になっています。

今回、上図のように、六角形の１つの頂点を１つの三角格子点（黒点）と一致するようにとり、その他の2つの頂点（赤点）がそれぞれ隣接する３つの三角格子の重心との一致するようにとります。また、六角形の3つの頂点（黒点および赤点）のそれぞれの内角は120°になるように設定します。あと、上図の\(r_1\)は基本図形の形を見ながら、調整していきます。

IH16（P31M）の基本図形を並べる

このIH16（P31M）の基本図形をP31M群の対称性を保ちながら並べると、以下のような図形が得られます。

IH16（P31M）による図形

IH16（P31M）の基本図形の変形

基本図形の変形を行うために、基本図形の各辺にラベルをふって、隣り合う基本図形との辺の対応関係を見てみます。

IH16（P31M）の基本図形に対する辺のラベルと向き

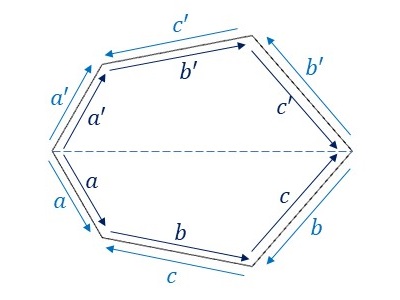
辺\(a\)と辺\(a’\)、辺\(b\)と辺\(b’\)、辺\(c\)と辺\(c’\)はそれぞれ同じ辺となります。

辺\(b\)と辺\(c\)が異なる向きに重なっていますので、辺\(b\)を変形し、辺\(c\)は変形した辺\(b\)を上下左右反転した形状に変形します。辺\(a\)は両側のラベルが同じで向きも同じになっています。これは、辺\(a\)が変形できないことを示しています。これらの変形により、隣り合う基本図形同士を重ねることなくP31G群の対称性に従って敷き詰めることができます。

ここでは、書籍「装飾パターンの法則」のp.96にあるIH16（P31M）の例を参考に、このルールに従ってIH16（P31M）の基本図形を下図のように変形してみました。

IH16（P31M）の基本図形の変形

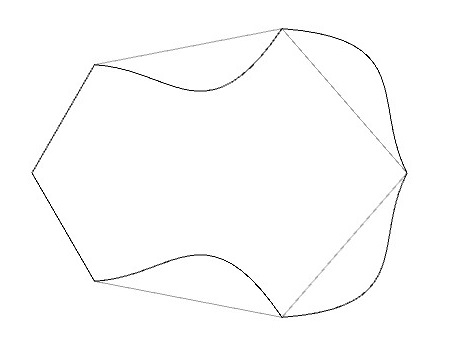
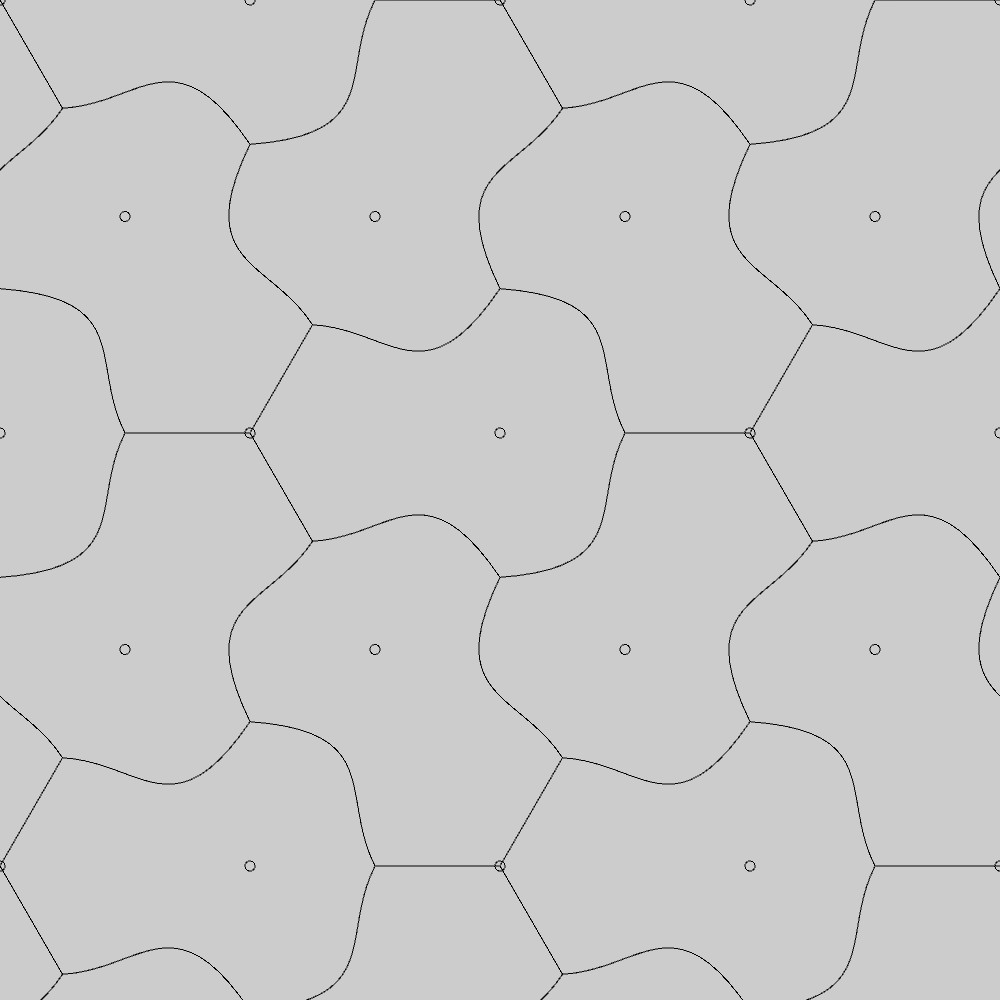
この変形した基本図形をP31M群の対称性を考慮して並べていくと、下図のような図形を得ることができます。なお、今回は三角格子点も示しています。

IH16（P31M）の変形した基本図形による図形

プログラムコード

今回の図形を作成するためのプログラムコードを示します。

PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
PVector[] base = new PVector[2]; // 格子を張るベクトル
int col_num = 4; // 描画するタイルの列の数
float scalar; // タイルの辺の長さ

void setup(){

  size(1000, 1000, P2D);
  noFill();
  scalar = width * 1.0 / col_num; // 描画ウィンドウと行の数からタイルの大きさを決定
  makeTriangleVector(); // 三角格子を張るベクトルの生成
  makeLattice(); // 格子点ベクトルを生成
  makeTileP31M(); // タイルを生成
  drawTiling(); // タイリングを描画

  save("IH16_P31M_transformation.jpg");
}

// 三角格子を張るベクトルを生成する関数
void makeTriangleVector(){
  base[0] = PVector.fromAngle(0.0);
  base[1] = PVector.fromAngle(PI / 3);
}

// 三角格子を生成する関数
void makeLattice(){
  int row_num = ceil(col_num / base[1].x); // 行の数
  lattice = new PVector[col_num + 3][row_num + 1];
  for (int i = 0; i < col_num + 3; i++){
    for (int j = 0; j < row_num + 1; j++){
      PVector v = PVector.mult(base[0].copy(), i * scalar); 
      v.add(PVector.mult(base[1].copy(), j * scalar));
      if(j%4 == 0){
        lattice[i][j] = new PVector(v.x - (j/2) * scalar, v.y);
      } else {
        lattice[i][j] = new PVector(v.x - (j/2+1) * scalar, v.y);
      }
    }
  }
}

// 六角形を変形する関数（基本図形）
PShape transformHexagon(){
  
  PVector[] v = new PVector[6]; // 六角形の頂点
  float r1;
  r1 = 1.0/2.0 * scalar;

  v[0] = new PVector(0.0, 0.0);
  v[1] = new PVector(r1, 0.0);
  v[1].rotate(radians(60));
  v[2] = new PVector(scalar, scalar / sqrt(3.0));
  v[3] = v[1].copy().sub(v[2].copy());
  v[3].rotate(radians(120));
  v[3].add(v[2].copy());
  v[4] = new PVector(scalar, -scalar / sqrt(3.0));
  v[5] = new PVector(r1, 0.0);
  v[5].rotate(-radians(60));

  // 六角形を変形する
  PShape hexagon = createShape();
  hexagon.beginShape(); 
  PVector[] auxiliary_point = new PVector[11];
  // 辺aは変形しない
  hexagon.vertex(v[0].x, v[0].y);
  hexagon.vertex(v[1].x, v[1].y);
  // 辺bを変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 2.0/5.0, -1.0/10.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 1.0/2.0, -1.0/2.0);
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[2].x, v[2].y); 
  // 辺cは辺bと同じ形を上下左右反転した形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 1.0/2.0, 1.0/2.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 3.0/5.0, 1.0/10.0);
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[3].x, v[3].y); 
  // 辺c'を辺cと同じ形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[3], v[4], 2.0/5.0, 1.0/10.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[3], v[4], 1.0/2.0, 1.0/2.0);
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[4].x, v[4].y); 
  // 辺b'を辺bと同じ形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[4], v[5], 1.0/2.0, -1.0/2.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[4], v[5], 3.0/5.0, -1.0/10.0);
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[5].x, v[5].y); 
  // 辺a'は変形しない
  hexagon.vertex(v[0].x, v[0].y);  
  
  hexagon.endShape();
  
  return hexagon;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

// タイルを生成する関数
void makeTileP31M(){
  tile = createShape(GROUP); // PShapeのグループを作る
  for (int i=0; i<3; i++){
    PShape hexagon = transformHexagon(); // 変形した六角形の生成
    hexagon.rotate(2 * PI * i / 3); // 120度回転
    if( i != 0 ){
      hexagon.translate(2.0 * scalar * base[i-1].x, 2.0 * scalar * base[i-1].y); // 組み合わせて正六角形となるようにシフト
    }
    tile.addChild(hexagon); // グループに追加
  }
}

// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
//  background(255);
  for (int i=0; i<lattice.length; i++){
    for (int j=0; j<lattice[0].length; j++){
      if( i%2 == 0 && j%2 == 0 ){
        tile.resetMatrix();
        tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
        shape(tile); // タイルを描画
      }
    }
  }
  
  // 格子点を描く
  for (int i=0; i<lattice.length; i++){
    for (int j=0; j<lattice[0].length; j++){
      circle(lattice[i][j].x, lattice[i][j].y, 10);
    }
  }
}

コメントを残す