リチュース螺旋

ここでは、書籍「アートで魅せる数学の世界」のp.139の図3.41に示してある、リチュース螺旋を再現してみました。

リチュース螺旋

今回再現してみたリチュース螺旋は以下のような図形になります。

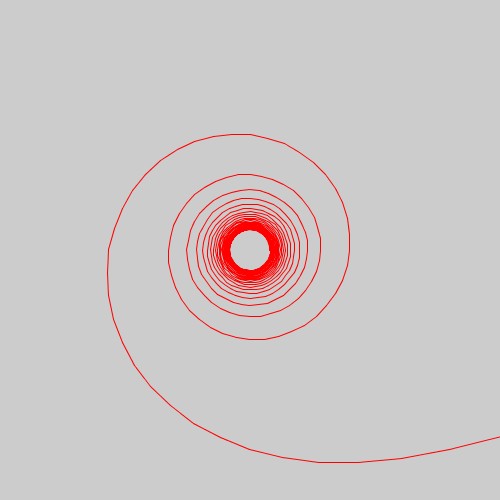
リチュース螺旋の式

リチュース螺旋の式は、\[ x(t) = \frac{a}{\sqrt{\theta}} \cos \theta, \ \ y(t) = \frac{a}{\sqrt{\theta}} \sin \theta \]で表されます。今回も糸掛けバージョンのように、\( \theta \to 2 \pi i N / M \)と置き換えて\[ x_i = a \sqrt{\frac{ M }{2 \pi i N}} \cos ( 2 \pi i N / M ), \ \ y_i = a \sqrt{\frac{ M }{2 \pi i N}} \sin ( 2 \pi i N / M ) \ \ ( i=1,2, \cdots, P) \]として\((x_i,y_i)\)を計算し、順にそれらの座標点を線分で結んでいくことでリチュース螺旋を描いています。ただし、\(i=0\)のときは計算できませんので、点列から外しています。

なお、今回は\( M=40, \ \ N=1, \ \ P=1000 \)として描いています。\(N\)の値を変えて糸掛けバージョンを試みてみましたが、リチュース螺旋では特に面白い図形は得られないようです。

ソースコード

リチュース螺旋のプログラムのソースコードを示しておきます。

void setup(){
  size(500,500);
  translate(width/2.0, height/2.0);
  noFill();

  // リチュース螺旋を描画
  stroke(255,0,0);
  drawLituusSpiral(250.0, 1.0, 40.0, 1000); 
}

// リチュース螺旋を描く関数
void drawLituusSpiral(
  float a, // 円の半径の初期値
  float N, // 糸掛係数
  float M, // 周期
  int P // データ数
){   
  float x, y, theta; 
  beginShape();
  for(int i=1; i<=P; i++){
    theta = 2.0 * PI * i * N / M;
    x = a / sqrt(theta) * cos( theta );
    y = a / sqrt(theta) * sin( theta );
    vertex(x,y);
  }
  endShape();
}