双曲螺旋

ここでは、書籍「アートで魅せる数学の世界」のp.139の図3.40に示してある、双曲螺旋を再現してみました。

双曲螺旋

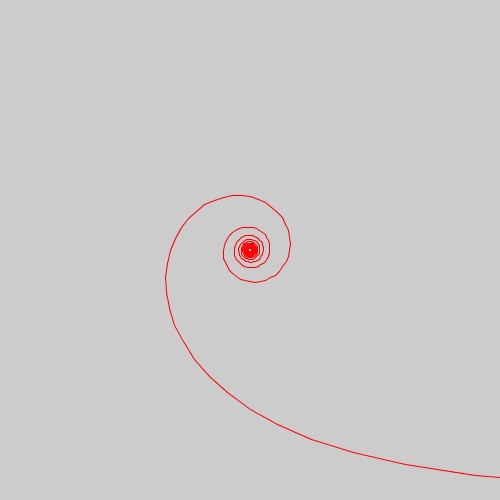
今回再現してみた双曲螺旋は以下のような図形になります。

双曲螺旋の式

双曲螺旋の式は、\[ x(t) = \frac{a}{\theta} \cos \theta, \ \ y(t) = \frac{a}{\theta} \sin \theta \]で表されます。今回も糸掛けバージョンのように、\( \theta \to 2 \pi i N / M \)と置き換えて\[ x_i = \frac{ a M }{2 \pi i N} \cos ( 2 \pi i N / M ), \ \ y_i = \frac{ a M }{2 \pi i N} \sin ( 2 \pi i N / M ) \ \ ( i=1,2, \cdots, P) \]として\((x_i,y_i)\)を計算し、順にそれらの座標点を線分で結んでいくことで双曲螺旋を描いています。ただし、\(i=0\)のときは計算できませんので、点列から外しています。

なお、今回は\( M=40, \ \ N=1, \ \ P=1000 \)として描いています。\(N\)の値を変えて糸掛けバージョンを試みてみましたが、双曲螺旋では特に面白い図形は得られないようです。

ソースコード

双曲螺旋のプログラムのソースコードを示しておきます。

void setup(){
  size(500,500);
  translate(width/2.0, height/2.0);
  noFill();

  // 双曲螺旋を描画
  stroke(255,0,0);
  drawHyperbolicSpiral(250.0, 1.0, 40.0, 1000); 
}

// 双曲螺旋を描く関数
void drawHyperbolicSpiral(
  float a, // 円の半径の初期値
  float N, // 糸掛係数
  float M, // 周期
  int P // データ数
){   
  float x, y, theta; 
  beginShape();
  for(int i=1; i<=P; i++){
    theta = 2.0 * PI * i * N / M;
    x = a / theta * cos( theta );
    y = a / theta * sin( theta );
    vertex(x,y);
  }
  endShape();
}