クロソイド曲線

ここでは、書籍「アートで魅せる数学の世界」のp.140の図3.42に示してある、クロソイド曲線（オイラー螺旋）を再現してみました。

クロソイド曲線

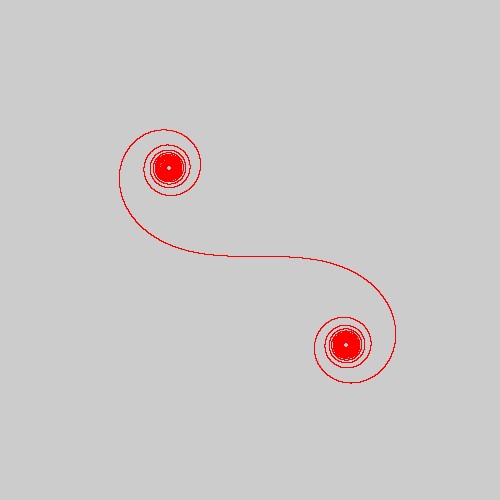
今回再現してみたクロソイド曲線は以下のような図形になります。

クロソイド曲線の式

クロソイド曲線の式は、微分方程式\[ \frac{d x(t)}{dt} = \cos \frac{t^2}{2}, \ \ \frac{d y(t)}{dt} = \cos \frac{t^2}{2} \]で表されます。この微分方程式を差分化により\[ x_{i+1} = x_i + \Delta t \cos \frac{t_i^2}{2}, \ \ y_{i+1} = y_i + \Delta t \sin \frac{t_i^2}{2}, \ \ t_i = ( i – \frac{P}{2} ) \Delta t \ \ ( i=0,1,2, \cdots, P) \]として\((x_i,y_i)\)を計算し、順にそれらの座標点を線分で結んでいくことでクロソイド曲線を描いています。また、糸掛係数\(N\)を導入して、\[ x_{i+1} = x_i + \Delta t \cos \frac{N t_i^2}{2}, \ \ y_{i+1} = y_i + \Delta t \sin \frac{N t_i^2}{2} \]とすると、糸掛けバージョンとすることができます。

上記のクロソイド曲線は\( N=1, \ \ P=80000 \)として描いています。

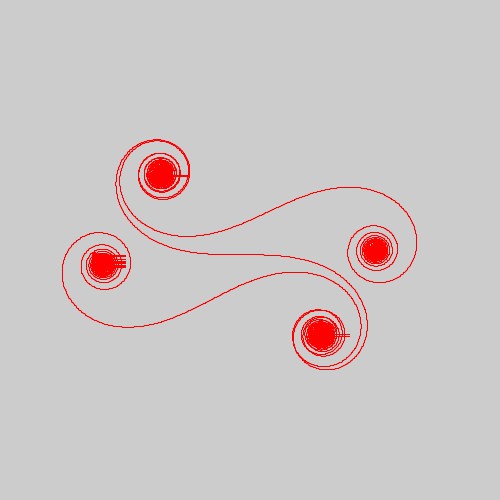
また、\( N=121, \ \ P=200000 \)とすると、書籍「アートで魅せる数学の世界」のp.142の図3.45のクロソイド曲線が得られます。

ソースコード

クロソイド曲線のプログラムのソースコードを示しておきます。

void setup(){
  size(500,500);
  translate(width * 1.0/3.0, height * 1.0/3.0);
  noFill();

  // クロソイド曲線（オイラー螺旋）を描画
  stroke(255,0,0);
  drawClothoidCurve(100.0, 1.0, 80000, 0.001); 
}

// クロソイド曲線（オイラー螺旋）を描く関数
void drawClothoidCurve(
  float a, // サイズを調整するパラメータ
  float N, // 糸掛係数
  int P, // データ数
  float dt // 測度
){   
  float x, y, t, start;
  x = 0.0;
  y = 0.0;
  start = - P * dt / 2.0;
  beginShape();
  for(int i=0; i<P; i++){
    t = start + dt * i;
    x += a * dt * cos( t *  t * N / 2.0 );
    y += a * dt * sin( t *  t * N / 2.0 );
    vertex(x,y);
  }
  endShape();
}