ここでは、書籍「アートで魅せる数学の世界」のp.135-142で解説されている螺旋のアートについて再現を試みています。
螺旋の描き方については記事「螺旋を描く」でも紹介していますが、今回は螺旋に「糸掛け」の技術を付加することでよりバリエーションの高い図形を描くことができます。
アルキメデス螺旋
書籍「アートで魅せる数学の世界」のp.137の図3.37左図に示してある、アルキメデス螺旋の糸掛けバージョンを再現してみました。

対数螺旋
書籍「アートで魅せる数学の世界」のp.137の図3.37右図に示してある、対数螺旋の糸掛けバージョンを再現してみました。

放物螺旋
書籍「アートで魅せる数学の世界」のp.138の図3.39に示してある、放物螺旋(フェルマー螺旋)の糸掛けバージョンとひまわりの種の配置を再現してみました。


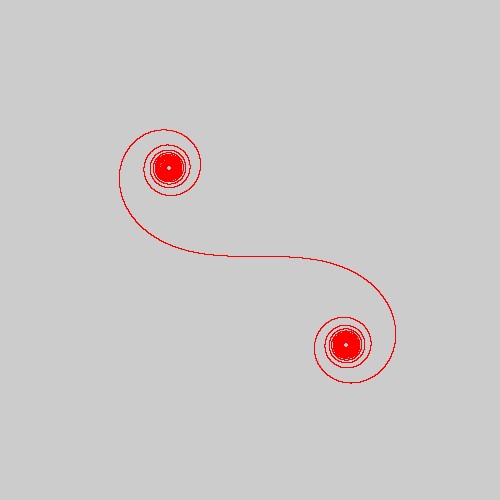
双曲螺旋
書籍「アートで魅せる数学の世界」のp.139の図3.40に示してある、双曲螺旋を再現してみました。
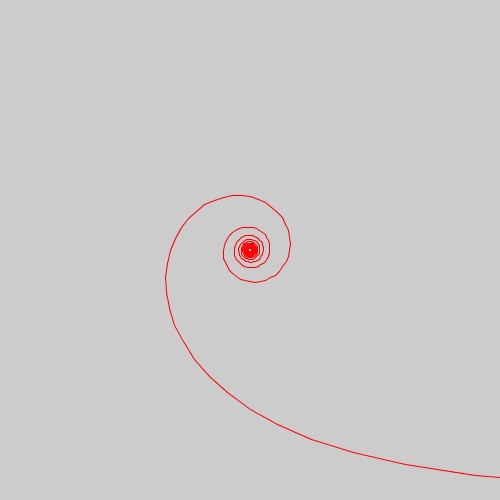
リチュース螺旋
書籍「アートで魅せる数学の世界」のp.139の図3.41に示してある、リチュース螺旋を再現してみました。
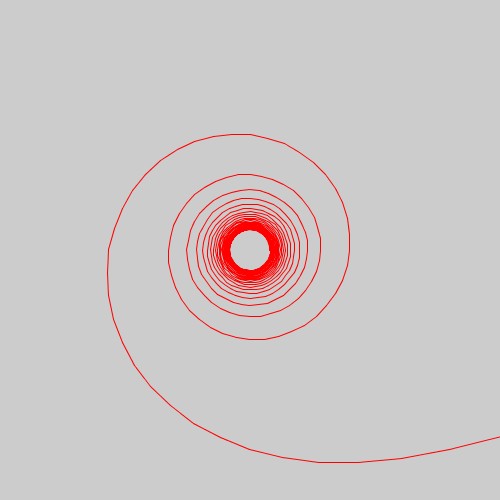
クロソイド曲線
書籍「アートで魅せる数学の世界」のp.140の図3.42に示してある、クロソイド曲線(オイラー螺旋)を再現してみました。