多項式型の数列

書籍「アートで魅せる数学の世界」のp.160で解説されている多項式型の数列を用いたストリング・アートについて再現を試みています。

Contents

1 多項式型の数列
2 \( \alpha = 2 \)の場合
- 2.1 ソースコード
3 \( \alpha = 3 \)の場合
- 3.1 失敗の原因は丸め誤差
- 3.2 ソースコード（修正版）

多項式型の数列は以下のようなものです。\[ s_4(i) = i^{\alpha} (i=0,1,2,\cdots,P) \]この数列によるストリング・アートを\(\alpha = 2\)の場合と\(\alpha = 3\)の場合とに分けて解説します。

\( \alpha = 2 \)の場合

まず、\( \alpha = 2 \)の場合の多項式型の数列によるストリング・アートを再現してみました。

ソースコード

多項式型の数列によるストリング・アートのプログラムのソースコードを示しておきます。

void setup(){
  size(500,500);
  translate(width/2.0, height/2.0);
  noFill();

  // 多項式型の数列によるストリング・アートを描画
  background(255,255,255);  

  int P = 1000;
  float[] s4 = makeSequence_s4(2.0, P);
  
  stroke(220,220,0);
  strokeWeight(0.1);  
  drawSequence(200.0, s4, 691.0, P);
}

// 多項式型の数列s4を生成する関数
float[] makeSequence_s4(
  float alpha,
  int P
){
  float[] s = new float[P+1];
  for(int i=0; i<=P; i++){
    s[i] = pow((float)i, alpha);
  }
  
  return s;
}

// 数列によるストリング・アートを描く関数
void drawSequence(
  float R, // 振幅
  float[] s, // 数列
  float M, // 周期
  int P // データ数
){   
  float x, y, theta; 
  beginShape();
  for(int i=0; i<=P; i++){
    theta = 2.0 * PI * s[i] / M;
    x = R * cos( theta );
    y = R * sin( theta );
    vertex(x,y);
  }
  endShape();
}

\( \alpha = 3 \)の場合

次に、\( \alpha = 3 \)の場合の多項式型の数列によるストリング・アートを再現してみました。上記に示したソースコードで\(\alpha=3\)として描きましたが、書籍「アートで魅せる数学の世界」のp.160の図3.76の下2つの図とは異なる結果となりました。

失敗の原因は丸め誤差

\( \alpha = 3 \)の場合の多項式型の数列によるストリング・アートの描画で失敗した理由は、どうも丸め誤差が原因のようです。例えば、\(999^3\)をProcessingで2通りの方法で計算してみます。

println(999*999*999); // int型の999を3回掛ける
println(pow(999.0,3.0)); // float型の999.0をpow関数で3乗する

結果は、

997002999
9.9700301E8

となります。つまり、float型では有効数字が7桁であるため丸め誤差が生じており、int型で計算した数「\(997002999\)」と異なる値になります。この丸め誤差の発生を抑える形でソースコードを修正した結果、以下のように書籍「アートで魅せる数学の世界」のp.160の図3.76の下2つの図と同じ結果を得ることができました。

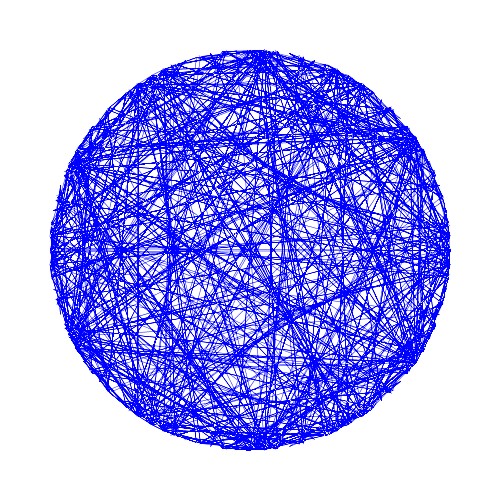
ソースコード（修正版）

\(\alpha=3\)の場合にも対応できるように修正した、多項式型の数列によるストリング・アートのプログラムのソースコードを示しておきます。

void setup(){
  size(500,500);
  translate(width/2.0, height/2.0);
  noFill();

  // 多項式型の数列によるストリング・アートを描画
  background(255,255,255);  

  int P = 1000;
  float M = 330.0;
  float[] s4 = makeSequence_s4_rev2(3, M, P);
  
  stroke(0,0,255);
  strokeWeight(0.5);  
  drawSequence(200.0, s4, M, P);
}

// 多項式型の数列s4を生成する関数（修正バージョン）
float[] makeSequence_s4_rev2(
  int alpha,
  float M,
  int P
){
  int m = (int)M;
  int s_temp;
  float[] s = new float[P+1];
  for(int i=0; i<=P; i++){
    s_temp = 1;
    for(int j=0; j<alpha; j++){ 
      s_temp *= i;
    }
    s[i] = (float)(s_temp % m);
  }
  
  return s;
}

// 数列によるストリング・アートを描く関数
void drawSequence(
  float R, // 振幅
  float[] s, // 数列
  float M, // 周期
  int P // データ数
){   
  float x, y, theta; 
  beginShape();
  for(int i=0; i<=P; i++){
    theta = 2.0 * PI * s[i] / M;
    x = R * cos( theta );
    y = R * sin( theta );
    vertex(x,y);
  }
  endShape();
}