書籍「アートで魅せる数学の世界」のp.156-159で解説されている場合分け型の数列を用いたストリング・アートについて再現を試みています。
場合分け型の数列1
1つ目の場合分け型の数列は以下のようなものです。\[ s_1(i) = \begin{cases} 0 & (i \text{が偶数}) \\ i & (i \text{が奇数}) \end{cases} \]この数列によるストリング・アートは以下のようになります。

場合分け型の数列2(コラッツ予想)
2つ目の場合分け型の数列は以下のようなものです。\[ s_2(i) = \begin{cases} i/2 & (i \text{が偶数}) \\ 3i+1 & (i \text{が奇数}) \end{cases} \]この数列によるストリング・アートは以下のようになります。

場合分け型の数列3
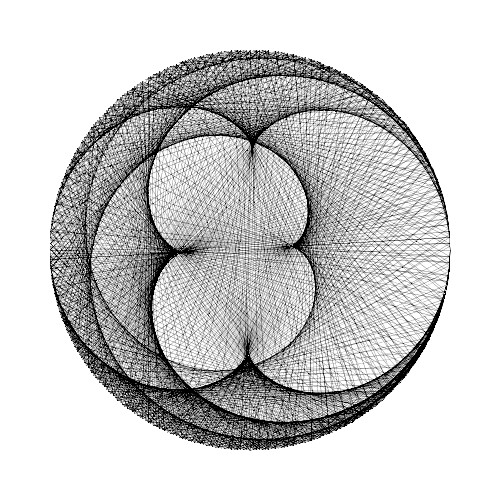
2つ目の場合分け型の数列は以下のようなものです。\[ s_2(i) = \begin{cases} ai & (i \text{が3の倍数}) \\ bi & (i \text{が3で割って1余る}) \\ ci & (i \text{が3で割って2余る}) \end{cases} \]この数列によるストリング・アートは以下のようになります。
ソースコード
場合分け型の数列によるストリング・アートのプログラムのソースコードを示しておきます。
void setup(){
size(500,500);
translate(width/2.0, height/2.0);
noFill();
// 場合分け型の数列によるストリング・アートを描画
background(255,255,255);
int P = 1000;
float[] s3 = makeSequence_s3(1.0, 2.0, 3.0, P);
stroke(0,0,0);
strokeWeight(0.1);
drawSequence(200.0, s3, 400.0, P);
}
// 数列s3を生成する関数
float[] makeSequence_s3(
float a,
float b,
float c,
int P
){
float[] s = new float[P+1];
for(int i=0; i<=P; i++){
if( i%3 == 0 ){
s[i] = a*i;
} else if (i%3 == 1){
s[i] = b*i;
} else {
s[i] = c*i;
}
}
return s;
}
// 数列を用いたストリング・アートを描く関数
void drawSequence(
float R, // 振幅
float[] s, // 数列
float M, // 周期
int P // データ数
){
float x, y, theta;
beginShape();
for(int i=0; i<=P; i++){
theta = 2.0 * PI * s[i] / M;
x = R * cos( theta );
y = R * sin( theta );
vertex(x,y);
}
endShape();
}