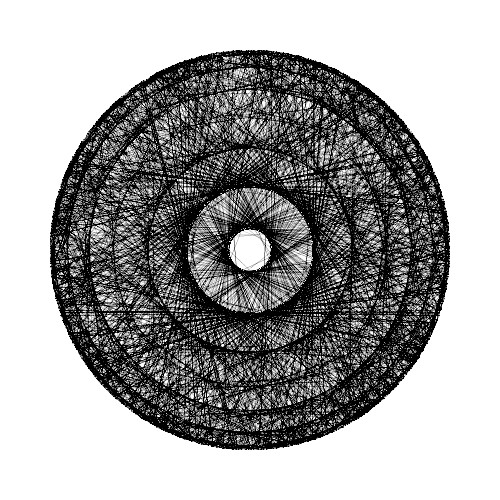
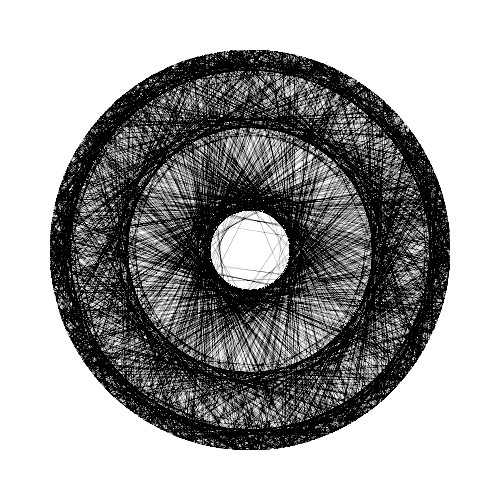
ここでは、書籍「アートで魅せる数学の世界」のp.155-162で解説されている様々な数列を用いたストリング・アートについて再現を試みています。
数列によるストリング・アート
これまでのストリング・アートは、与えられた座標の式\( ( x(\theta), y(\theta) ) \)に対して、\(\theta \to 2 \pi i N / M \)のようにパラメータを変更することで糸掛けバージョンとしていましたが、今回は、数列\( s(i) \ \ ( i=0,1,2, \cdots , P) \)を用いて、\(\theta \to 2 \pi s(i) / M \)と置き換えて糸掛けバージョンを作ることを考えます。なお、ここで扱う座標の式は\[ x(\theta) = R \cos \theta, \ \ y(\theta) = R \sin \theta \]となります。
場合分け型の数列
書籍「アートで魅せる数学の世界」のp.156-159で解説されている場合分け型の数列を用いたストリング・アートについて再現を試みています。


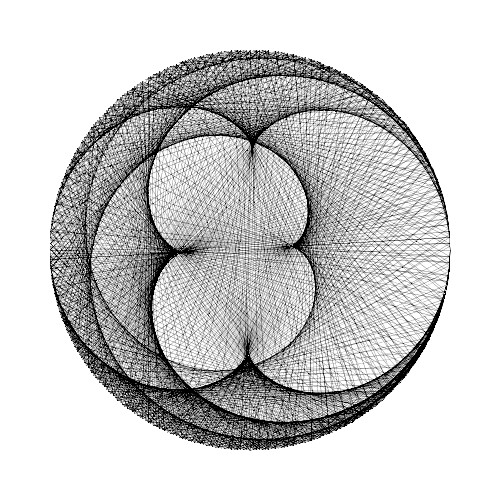
多項式型の数列
書籍「アートで魅せる数学の世界」のp.160で解説されている多項式型の数列を用いたストリング・アートについて再現を試みています。


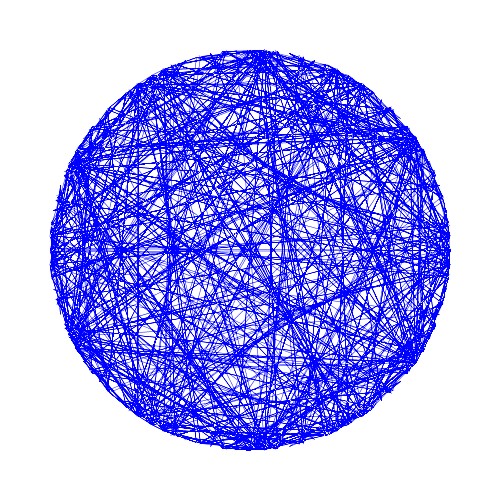
素数列
書籍「アートで魅せる数学の世界」のp.161-162で解説されている素数列を用いたストリング・アートについて再現を試みています。