糸掛け曼荼羅

ここでは、書籍「アートで魅せる数学の世界」のp.126-135で解説されている糸掛け曼荼羅について再現を試みています。

糸掛け曼荼羅

糸掛け曼荼羅とは以下のような図形になります。

なお、これら3つの糸掛け曼荼羅は、書籍「アートで魅せる数学の世界」のp.130の図3.27をProcessingを利用して再現したものになります。

糸掛け曼荼羅の考え方

糸掛け曼荼羅の考え方について説明します。

まず、円を考え、その円周上に等間隔に\(M\)個の点を打ちます。そのうちの任意の1点と、その点から時計回り（または反時計回り）に回った\(N\)個先の点とを線で結びます。次に、先ほど選んだ\(N\)個先の点と、さらにその点から\(N\)個先に進んだ点とを線で結びます。この操作を繰り返していくことで、糸掛け曼荼羅と呼ばれる美しい図形を得ることができます。

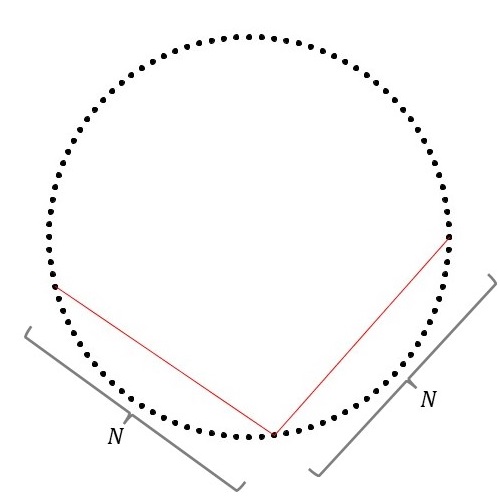
以上のことを数式で表すと、以下のように簡単な式で表すことができます。\[ x_i = r \cos ( 2 \pi i N / M ), \ \ y_i = r \sin ( 2 \pi i N / M ) \ \ ( i = 0, 1, 2, \cdots, P ) \]つまり、\( (x_i, y_i) \)を計算し、順にそれらの座標点を線分で結んでいくことで糸掛け曼荼羅を描くことができます。なお、\(r\)は基になる円の半径、\(P+1\)は糸掛け曼荼羅の頂点の数になります。

パラメータ\(M, N, P \)の選択によって、様々な形の糸掛け曼荼羅を描くことができます。例えば、書籍「アートで魅せる数学の世界」では他に\(M\)が無理数の場合などが紹介されています。

糸掛け曼荼羅を重ねる

糸掛け曼荼羅はいくつかの糸掛け曼荼羅を重ね合わせるとよりきれいな図形を描くことができます。ここでは、上記で示した３つの糸掛け曼荼羅を重ね合わせてみました。

ソースコード

最後に、糸掛け曼荼羅を描くプログラムのソースコードを示しておきます。

void setup(){
  size(500,500);
  translate(width/2.0, height/2.0);
  noFill();

  // 3つの糸掛け曼荼羅を色を変えて重ねる
  stroke(255,0,0);
  drawMandala(200.0, 23.0, 100.0, 100);
  stroke(0,255,0);
  drawMandala(200.0, 23.0, 60.0, 100); 
  stroke(0,0,255);
  drawMandala(200.0, 23.0, 150.0, 100); 

}

void drawMandala(
  float r, // 円の半径
  float N, // 糸掛係数
  float M, // 周期
  int P // データ数
){   
  float x, y; 
  beginShape();
  for(int i=0; i<=P; i++){
    x = r * cos( 2.0 * PI * i * N / M);
    y = r * sin( 2.0 * PI * i * N / M);
    vertex(x,y);
  }
  endShape();
}