ハイポトロコイド

ここでは、書籍「アートで魅せる数学の世界」のp.147-150で紹介されている、ハイポトロコイドの糸掛けバージョンを再現してみました。

ハイポトロコイド

今回再現してみたハイポトロコイドは以下のような図形になります。

ハイポトロコイドとは

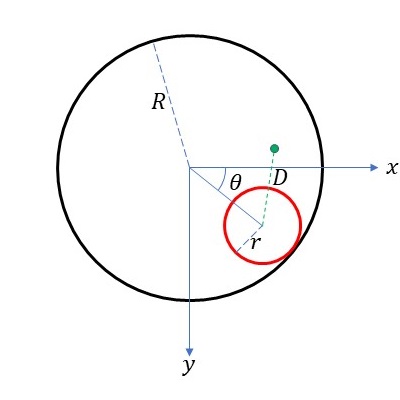
ハイポトロコイドとは、半径\(R\)の大きな円の内周を半径\(r\)の小さな円が滑らずに転がっていくときに、小さな円の中心から距離\(D\)だけ離れた一点が描く軌跡のことを言います。これは、ハイポサイクロイドの拡張版ということができると思います。

ハイポトロコイドの式

ハイポトロコイドの式は、上図の\(D\)を小さい円の半径との比として\(D = r / d\)と表すと、\[ x = (R-r) \cos \theta + \frac{r}{d} \cos \left( \frac{R-r}{r} \theta \right), \ \ y = (R-r) \sin \theta – \frac{r}{d} \sin \left( \frac{R-r}{r} \theta \right) \]で表されます。今回は糸掛けバージョンとなりますので、\( \theta \to 2 \pi i N / M \)と置き換えて、\[ x_i = (R-r) \cos \frac{2 \pi i N}{M} + \frac{r}{d} \cos \left( \frac{R-r}{r} \frac{2 \pi i N}{M} \right), \ \ y_i = (R-r) \sin \frac{2 \pi i N}{M} – \frac{r}{d} \sin \left( \frac{R-r}{r} \frac{2 \pi i N}{M} \right) \ \ ( i=0,1,2, \cdots, P) \]として\((x_i,y_i)\)を計算し、順にそれらの座標点を線分で結んでいくことでハイポトロコイドの糸掛けバージョンを描くことができます。

上記のハイポトロコイドは\( M=100, \ \ N=1, \ \ R=234, \ \ r=138, \ \ d=2 \)として描いています。

ハイポトロコイド×糸掛け

書籍「アートで魅せる数学の世界」のp.150で紹介されている、ハイポトロコイドの糸掛けバージョンを再現してみました。

まず、図3.59の2つの図形を再現します。

次に、図3.60の2つの図形を再現します。背景を黒色、線を白色で描き、また線を細く描くことで神秘的な図形を描くことができます。

ソースコード

ハイポトロコイドの糸掛けバージョンのプログラムのソースコードを示しておきます。

void setup(){
  size(500,500);
  translate(width/2.0, height/2.0);
  noFill();

  // ハイポトロコイドを描画
  background(255,255,255);  
  stroke(0,0,255);
  strokeWeight(1.0);  
  drawHypotrochoid(6.0*39.0,6.0*23.0, 2.0, 1.0, 100.0, 10000); 
}

// ハイポトロコイドを描く関数
void drawHypotrochoid(
  float R, // 大きい円の半径
  float r, // 小さい円の半径
  float d, // 点の位置（小さい円の半径との比）
  float N, // 糸掛係数
  float M, // 周期
  int P // データ数
){   
  float x, y, theta; 
  beginShape();
  for(int i=1; i<=P; i++){
    theta = 2.0 * PI * i * N / M;
    x = (R-r) * cos( theta ) + (r/d) * cos( (R-r)/r * theta );
    y = (R-r) * sin( theta ) - (r/d) * sin( (R-r)/r * theta );
    vertex(x,y);
  }
  endShape();
}