ここでは、正四面体を例にして立体視の原理を説明したいと思います。なお、ここでの解説は書籍「ステレオグラムをつくろう―あなたも3Dアーティスト」のp.46を参考にしています。
Contents
正四面体
正四面体とは、下図のように正三角形4枚を組み合わせて作る、立体図形となります。
今回は、この正四面体を\(z\)軸方向から見て紙から飛び出してみえるように平面上に立体視用の図形を描いてみます。
立体視の原理
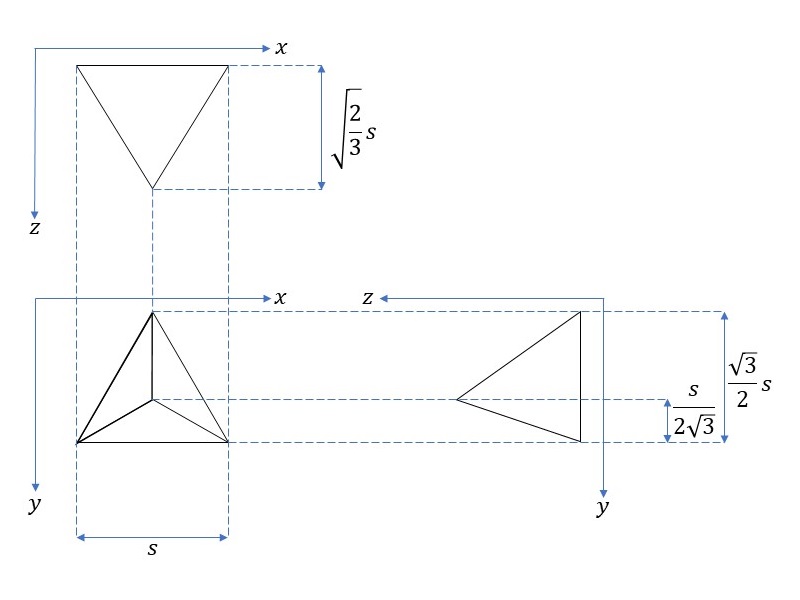
立体視の原理を説明するために、正四面体を三面図で表しておきます。
立体視の原理(横方向)
まず立体視の横方向に関してその原理を説明したいと思います。ここで、横方向と縦方向とは人間の両目を結んだ方向を横方向(座標軸で言えば\(x\)軸方向)と呼び、その方向に垂直となる方向を縦方向(座標軸で言えば\(y\)軸方向)と呼ぶことにします。
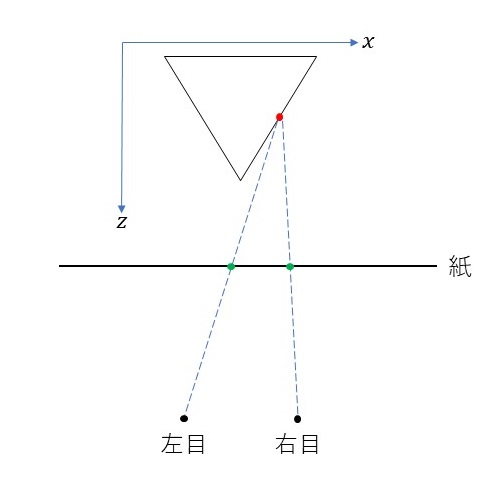
正四面体上のある一点(赤点)を\(z\)軸方向から見ることを考えます。そのときの両目の位置を上図のように配置します(黒点)。両目から赤点をみるときの視線は点線のようになります。ここで、両目と正四面体の間に紙をはさみます。このとき、赤点をみるときの視線と紙が交わる点は緑色の点のようになります。これら左目用の緑色の点と右目用の緑色の点を紙上にプロットします。これで立体視を行う準備は完了です。つまり、紙上にプロットした左目用の点を左目で、右目用の点を右目でみて、焦点をうまく合わせることで、あたかも赤点の部分が紙面から浮き出たように見ることができます。
立体視の原理(縦方向)
次に立体視の縦方向に関してみてみます。
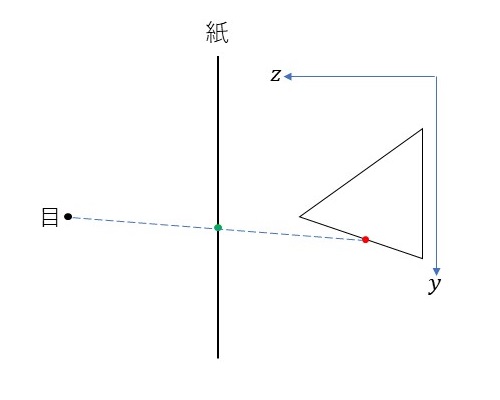
横方向のときと同様に、正四面体上のある一点(赤点)を\(z\)軸方向から見ることを考えます。そのときの両目の縦方向の位置は左右同じ高さになりますので、上図のように配置します(黒点)。目から赤点をみるときの視線は点線のようになります。ここで、両目と正四面体の間に紙をはさみます。このとき、赤点をみるときの視線と紙が交わる点は緑色の点のようになります。つまり、紙上にプロットした左目用の点と右目用の点の縦方向の位置は同じ高さになるようにとる必要があることが分かります。
立体視用の図形
立体視用の図形を描く準備(横方向)
上記の立体視の原理を利用して、実際に紙上に立体視用の図形を描いていきます。そのために紙上に描かれる左目用の点と右目用の点の位置を算出します。
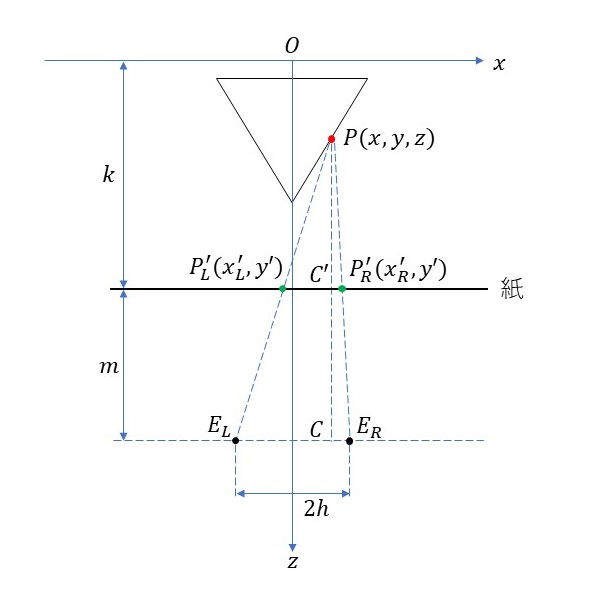
\(z\)軸が正四面体の一つの頂点を通るように、座標系を設定します。また、紙は\(xy\)平面と平行になるように設定し、両目の位置を結んだ線\(E_LE_R\)は\(x\)軸と平行になるように設定します(上図)。そして、紙と\(xy\)平面との間の距離を\(k\)とし、紙と目との間の距離を\(m\)、両目間の距離を\(2h\)とします。
立体視したい図形上の点(赤点)の位置を\(P(x,y,z)\)とし、左目の位置を\(E_L(-h,0,m+k)\)、右目の位置を\(E_R(h,0,m+k)\)とし、このとき紙上にプロットされる左目用の点を\(P’_L(x’_L,y’,k)\)、右目用の点を\(P’_R(x’_R,y’,k)\)とおきます。また、補助点として両目を結ぶ線上に位置して、点\(P\)と\(x\)座標が一致する点\(C(x,0,m+k)\)、およびこの点\(C\)と点\(P\)を結ぶ線と紙が交わる点を\(C'(x,y’,k)\)とします。
\(\bigtriangleup PCE_L\)と\(\bigtriangleup PC’P’_L\)は相似の関係になります。したがって、\(C’P’_L/CE_L = PC’/PC \)となるので、
\[ \frac{x’_L-x}{h+x} = \frac{k-z}{m+k-z} \]
となり、これから
\[ x’_L = \frac{mx+hz-hk}{m+k-z} \]
という計算式が得られます。同様に、\(\bigtriangleup PCE_R\)と\(\bigtriangleup PC’P’_R\)は相似の関係になります。したがって、\(C’P’_R/CE_R = PC’/PC \)となるので、
\[ \frac{x’_R-x}{h-x} = \frac{k-z}{m+k-z} \]
から
\[ x’_R = \frac{mx-hz+hk}{m+k-z} \]
という計算式が得られます。
立体視用の図形を描く準備(縦方向)
次に紙上に描かれる点の縦方向(\(y\)軸方向)の位置を算出します。
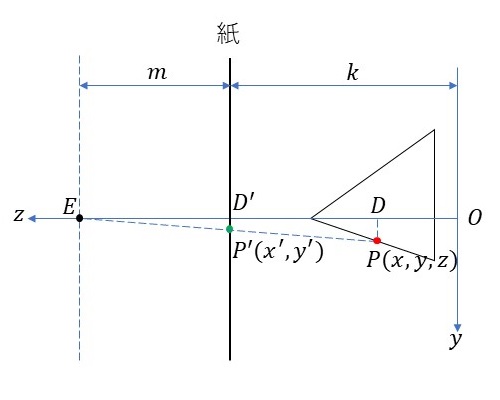
立体視したい図形上の点(赤点)の位置を\(P(x,y,z)\)とします。この場合、左目も右目も同じ高さになりますので、左目の位置も右目の位置も共通して\(E(\pm h, 0, m+h)\)とおき、紙上にプロットされる左目用の点の位置と右目用の点の位置も\(P'(x’,y’,k)\)とおきます。また、補助点として点\(P\)から\(xz\)平面への垂線が交わる点を\(D(x,0,z)\)、およびこの点\(D\)と点\(E\)を結ぶ線と紙が交わる点を\(D'(x’,0,k)\)とします。
\(\bigtriangleup EDP\)と\(\bigtriangleup ED’P’\)は相似の関係になります。したがって、\(D’P’/DP = ED’/ED \)となるので、
\[ \frac{y’}{y} = \frac{m}{m+k-z} \]
となり、これから
\[ y’ = \frac{my}{m+k-z} \]
という計算式が得られます。
立体視用の図形を描いてみる
以上で立体視用の図形を描くための準備が整いました。後は立体視したい立体図形(ここでは正四面体)上の各点に対して、左目用の点\(P’_L(x’_L,y’,k)\)、右目用の点\(P’_R(x’_R,y’,k)\)を計算して紙上にプロットしていくだけになります(紙上にプロットする際には\(z\)軸方向の値は無視します。)。
実際に、正四面体の立体視用に図形を作ってみます。なお、正四面体上のすべての点を対象にすることは大変なので、今回は正四面体の辺上に乗っている点に着目して描いてみました。

この画像を紙に印刷して、紙と目を近づけていってください。そうすると、紙上の2つの正四面体が3つの正四面体に見えるようになってきます。その真ん中の正四面体は最初2つの像が重なってずれて見えますが、1つの像に見えるように少し根気強く目のピントを合わせてみてください。ピントが合うと、真ん中の正四面体が立体的に見えるはずです。
プログラムコード
今回の正四面体の立体視用の図形を描くためのプログラムコード(Processing)を示しておきます。
void setup(){
size(1000,500,P2D);
background(255,255,255);
float k = 500.0; // 座標原点から紙までの距離
float m = 500.0; // 紙から目までの距離
float h = 150.0; // 目と目の間の距離の半分
PVector point3d; // 立体視したい図形上の点
float x_r, x_l, y_eye; // 紙上の点
float triangular_pyramid_size = 200.0; // 正四面体のサイズ
// 三角錐の4つの頂点のベクトル
PVector triangular_pyramid[] = new PVector[4];
triangular_pyramid[0] = new PVector(0.0, 0.0, sqrt(2.0/3.0)*triangular_pyramid_size);
triangular_pyramid[1] = new PVector(0.0, -1.0/sqrt(3.0)*triangular_pyramid_size, 0.0);
triangular_pyramid[2] = triangular_pyramid[1].copy().rotate(radians(120));
triangular_pyramid[3] = triangular_pyramid[1].copy().rotate(radians(240));
translate(width/2, height/2);
// 紙の上に正四面体を射影する
for(int i=0; i<4; i++){
for(int j=i+1; j<4; j++){
for(int d=0; d<100; d++){
point3d = triangular_pyramid[i].copy().add(triangular_pyramid[j].copy().sub(triangular_pyramid[i].copy()).mult(d/100.0));
x_r = (m * point3d.x - h * point3d.z + h*k) / (m + k - point3d.z);
x_l = (m * point3d.x + h * point3d.z - h*k) / (m + k - point3d.z);
y_eye = m * point3d.y / (m + k - point3d.z);
point(x_r, y_eye);
point(x_l, y_eye);
}
}
}
save("stereogram_triangular_pyramid.jpg");
}