文字「ステレオ」

  1. ホーム
  2. 立体視（ステレオグラム）
  3. 文字「ステレオ」

ここでは、空間上に浮かんだような文字の立体図形をランダムドット・ステレオグラムで再現してみたいと思います。なお、この作品は書籍「ステレオグラムをつくろう―あなたも3Dアーティスト」のp.58を参考にしています。

文字「ステレオ」

今回は「ステレオ」という文字をランダムドット・ステレオグラムで作成したいと思います。そのために下記のような画像を準備しました。

文字「ステレオ」の画像

文字「ステレオ」のランダムドット・ステレオグラム

今回作成した文字「ステレオ」のランダムドット・ステレオグラムは次のようになりました。

文字「ステレオ」のランダムドット・ステレオグラム

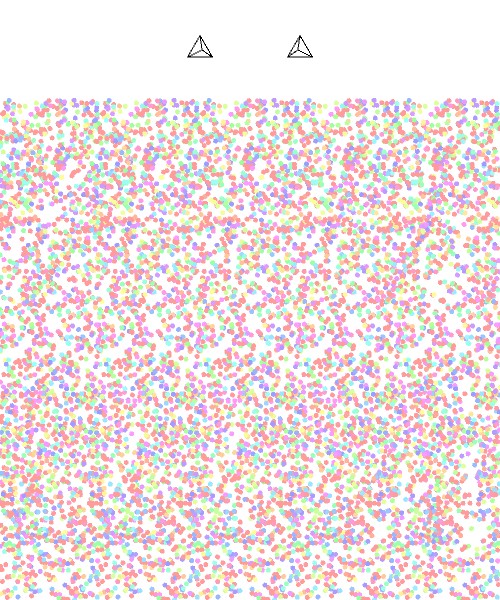
この画像を紙に印刷してじっと眺めてみてください。文字「ステレオ」が浮かび上がってくるはずです。ランダムドット・ステレオグラムの見方については、記事「ランダムドット・ステレオグラム」で解説していますので、そちらもご覧ください。

視線と文字との交点の算出

ランダムドット・ステレオグラムの作成方法については、記事「ランダムドット・ステレオグラム」で解説しています。この文字形状をランダムドット・ステレオグラム化するにあたってのポイントは、目の位置と紙上の点の位置との延長線上に文字との交点を求めるところですが、比較的簡単に求めることができます。

  1. 文字を浮かして表示するときの高さ（\(z\)方向の位置）を決める。
  2. 目の位置と紙上の点の位置との延長線と1で決めた高さにある平面との交点を求める。
  3. 2で求めた交点の\(xy\)座標位置にある文字画像の画素を調べて、その画素が文字上の画素であれば2で求めた交点をそのまま利用し、文字上の画素でなければ交点を目の位置と紙上の点の位置との延長線と\(z=0\)の平面との交点に更新する。

プログラムコード

文字「ステレオ」のランダムドット・ステレオグラムを作成したときのプログラムコード（Processing）を載せておきます。

float k = 500.0; // 座標原点から紙までの距離
float m = 500.0; // 紙から目までの距離
float h = 100.0; // 目と目の間の距離の半分

float diff = 100.0; // 文字を浮かせる幅

void setup(){
  size(500,600,P2D);
  background(255,255,255);
  
  PVector point3d; // 立体視したい図形上の点
  float x_r, x_l, y_eye; // 紙上の点
  
  float triangular_pyramid_size = 50.0; // 三角錐のサイズ
  // 三角錐の4つの頂点のベクトル
  PVector triangular_pyramid[] = new PVector[4];
  triangular_pyramid[0] = new PVector(0.0, 0.0, sqrt(2.0/3.0)*triangular_pyramid_size);
  triangular_pyramid[1] = new PVector(0.0, -1.0/sqrt(3.0)*triangular_pyramid_size, 0.0);
  triangular_pyramid[2] = triangular_pyramid[1].copy().rotate(radians(120));
  triangular_pyramid[3] = triangular_pyramid[1].copy().rotate(radians(240)); 

  translate(width/2, 50);

  // 紙の上に三角錐を左目用と右目用にそれぞれ射影する

  for(int i=0; i<4; i++){
    for(int j=i+1; j<4; j++){
      for(int d=0; d<100; d++){
        point3d = triangular_pyramid[i].copy().add(triangular_pyramid[j].copy().sub(triangular_pyramid[i].copy()).mult(d/100.0)); 
        x_r = (m * point3d.x - h * point3d.z + h*k) / (m + k - point3d.z);
        x_l = (m * point3d.x + h * point3d.z - h*k) / (m + k - point3d.z);
        y_eye = m * point3d.y / (m + k - point3d.z);
        point(x_r, y_eye);
        point(x_l, y_eye);
      }
    }
  }
  translate(0, 300);

  // 文字画像を取り込む
  PImage img = loadImage("moji.jpg");
 
  float x_ini, y_ini;
  for(int i=0; i<2000; i++){
    colorMode(HSB);
    fill(random(360),100,1000);
    noStroke();

    x_ini = random(width)-width/2; // 紙上の点の初期値x座標
    y_ini = random(width)-width/2; // 紙上の点の初期値y座標

    // まず初期値が左目からの座標として処理する
    x_l = x_ini;
    y_eye = y_ini;
    ellipse(x_l, y_eye, 5, 5);
    while(true){
      // この左目からの位置に対応する対称物体の上の点の位置を算出する。
      point3d = get3Dpoint(img, x_l, y_eye, -h);
      // この対称物体上の点に対応する、右目からの紙上の座標位置を算出する。
      x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
      if( abs(x_r) < width/2.0 ){ 
        ellipse(x_r, y_eye, 5, 5);
        x_l = x_r;
      } else {
        break;
      }
    }
    
    // 次に初期値を右目からの座標として処理する
    x_r = x_ini;
    while(true){
      // この右目からの位置に対応する対称物体の上の点の位置を算出する。
      point3d = get3Dpoint(img, x_r, y_eye, h);
      // この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
      x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
      if( abs(x_l) < width/2.0 ){ 
        ellipse(x_l, y_eye, 5, 5);
        x_r = x_l;
      } else {
        break;
      }
    }
  }
      
  save("stereogram_moji.jpg");
  
}

PVector get3Dpoint(
  PImage img, // 元となる文字画像
  float x_on_paper, // 紙上の点のx座標
  float y_on_paper, // 紙上の点のy座標
  float eye_pos_x // 左目の場合-h, 右目の場合h
){
  float t = (m+k-diff)/m;
  float x, y, z;
  x = eye_pos_x + (x_on_paper - eye_pos_x)*t;
  y = y_on_paper * t;
  z = m + k - m * t;
  int loc = int(x) + img.width/2 + (int(y) + img.width/2) * img.width;
  if( red(img.pixels[loc]) < 128.0 ){
    t = (m+k)/m;
    x = eye_pos_x + (x_on_paper - eye_pos_x)*t;
    y = y_on_paper * t;
    z = m + k - m * t;
  }    

  PVector result = new PVector(x,y,z);
  return result;
}

コメントを残す