ここでは、真ん中が空いていて曲がった四角と丸が鎖のように絡み合った形状の立体図形をランダムドット・ステレオグラムで再現してみたいと思います。なお、この作品は書籍「ステレオグラムをつくろう―あなたも3Dアーティスト」のp.56を参考にしています。
四角と丸
今回、ランダムドット・ステレオグラムで作成する形状は以下のような立体図形を上から見たような図形となります。

四角と丸のランダムドット・ステレオグラム
今回作成した四角と丸のランダムドット・ステレオグラムは次のようになりました。

この画像を紙に印刷してじっと眺めてみてください。四角と丸の形状が浮かび上がってくるはずです。ランダムドット・ステレオグラムの見方については、記事「ランダムドット・ステレオグラム」で解説していますので、そちらもご覧ください。
視線と立体との交点の算出
ランダムドット・ステレオグラムの作成方法については、記事「ランダムドット・ステレオグラム」で解説しています。この四角と丸の形状をランダムドット・ステレオグラム化するにあたりポイントとなるところは、やはり目の位置と紙上の点の位置との延長線上に立体との交点を求めるところです。ただ、バウムクーヘンやたまごパックのときのようにニュートン法などを利用して数値的に求める必要はありません。以下に、四角と丸の立体図形の三面図を示します。
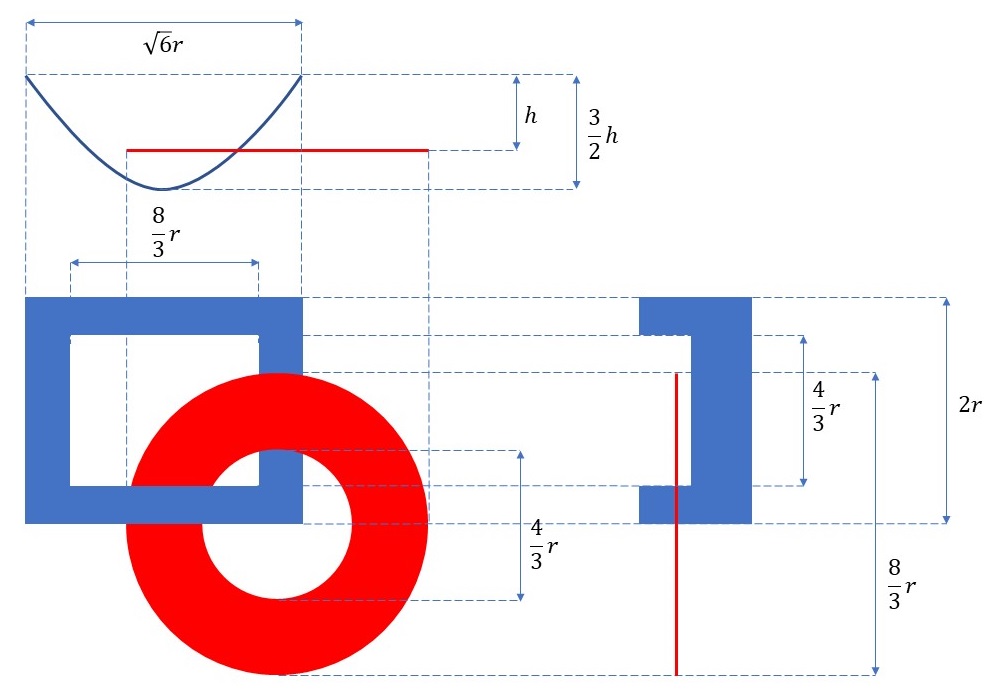
今回、四角形状の曲がった部分を2次関数で表すことにしました(左上図)。そのため、曲がった四角の形状と視線の交点は2次方程式を解けばよく、丸との交点も平面との交点となり計算で求めることができます。
ただし、交点については場合分けが必要になります。今回は以下のように考えました。
- 目の位置と紙上の点の位置との延長線と四角の部分と交点があるか確認する。
- 四角の部分との交点があれば、一旦この交点を交点候補として保持、交点でなければ改めて目の位置と紙上の点の位置との延長線と底面(\(z=0\)平面)の交点を求めて交点候補とする。
- 次に、目の位置と紙上の点の位置との延長線と丸の部分と交点があるか確認する。
- 丸の部分と交点があれば、この交点と2で求めた交点候補を比べて、\(z\)座標が大きい方を交点とする。丸の部分と交点がなければ、2で求めた交点候補を交点とする。
プログラムコード
四角と丸の形状のランダムドット・ステレオグラムを作成したときのプログラムコード(Processing)を載せておきます。
float k = 500.0; // 座標原点から紙までの距離
float m = 500.0; // 紙から目までの距離
float h = 100.0; // 目と目の間の距離の半分
float radius = 150.0; // 円の半径
float circle_pos_z = 100.0; // 円のz軸方向の位置
void setup(){
size(500,600,P2D);
background(255,255,255);
PVector point3d; // 立体視したい図形上の点
float x_r, x_l, y_eye; // 紙上の点
float triangular_pyramid_size = 50.0; // 三角錐のサイズ
// 三角錐の4つの頂点のベクトル
PVector triangular_pyramid[] = new PVector[4];
triangular_pyramid[0] = new PVector(0.0, 0.0, sqrt(2.0/3.0)*triangular_pyramid_size);
triangular_pyramid[1] = new PVector(0.0, -1.0/sqrt(3.0)*triangular_pyramid_size, 0.0);
triangular_pyramid[2] = triangular_pyramid[1].copy().rotate(radians(120));
triangular_pyramid[3] = triangular_pyramid[1].copy().rotate(radians(240));
// 三角錐の位置
translate(width/2, 50);
// 紙の上に三角錐を左目用と右目用にそれぞれ射影する
for(int i=0; i<4; i++){
for(int j=i+1; j<4; j++){
for(int d=0; d<100; d++){
point3d = triangular_pyramid[i].copy().add(triangular_pyramid[j].copy().sub(triangular_pyramid[i].copy()).mult(d/100.0));
x_r = (m * point3d.x - h * point3d.z + h*k) / (m + k - point3d.z);
x_l = (m * point3d.x + h * point3d.z - h*k) / (m + k - point3d.z);
y_eye = m * point3d.y / (m + k - point3d.z);
point(x_r, y_eye);
point(x_l, y_eye);
}
}
}
// ステレオグラムを描く位置
translate(0, 300);
float x_ini, y_ini;
for(int i=0; i<3000; i++){
colorMode(HSB);
fill(random(360),100,1000);
noStroke();
x_ini = random(width)-width/2; // 紙上の点の初期値x座標
y_ini = random(width)-width/2; // 紙上の点の初期値y座標
// まず紙上の点の初期値が左目からの座標として処理する
x_l = x_ini;
y_eye = y_ini;
ellipse(x_l, y_eye, 3, 3);
while(true){
// この左目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_l, y_eye, -h);
// この対称物体上の点に対応する、右目からの紙上の座標位置を算出する。
x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
if( abs(x_r) < width/2.0 ){
ellipse(x_r, y_eye, 3, 3);
x_l = x_r;
} else {
// 紙の範囲を外れたらループを抜ける
break;
}
}
// 次に紙上の点の初期値を右目からの座標として処理する
x_r = x_ini;
while(true){
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_r, y_eye, h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
if( abs(x_l) < width/2.0 ){
ellipse(x_l, y_eye, 3, 3);
x_r = x_l;
} else {
// 紙の範囲を外れたらループを抜ける
break;
}
}
}
save("stereogram_circleAndRect.jpg");
}
// 対称物体上の点の位置を算出する関数
PVector get3DPoint(
float x_on_paper, // 紙上の点のx座標
float y_on_paper, // 紙上の点のy座標
float eye_pos_x // 左目の場合-h, 右目の場合h
){
// 視点(左目or右目)と紙上の点を通る直線をパラメータ表示したときの係数
float ax = x_on_paper - eye_pos_x;
float bx = eye_pos_x;
float ay = y_on_paper;
float by = 0.0;
float az = -m;
float bz = m + k;
// 四角形が乗る曲面を2次関数で現したときの係数(z=-A(x+alpha)^2+B)
float A = circle_pos_z / radius / radius;
float B = circle_pos_z * 3.0 / 2.0;
float alpha = 2.0/3.0 * radius;
// 上記の直線と2次関数の曲面との交点を算出するための2次方程式の係数
float a = A * ax * ax;
float b = 2.0 * A * ax *(bx + alpha) + az;
float c = A*(bx + alpha) * (bx + alpha) + bz - B;
// 2次方程式の解
float t = (m+k)/m; // tの初期値(z=0平面と交わる時の値)、解がなければこの値を利用
float tp, zp, tm, zm;
if( b*b - 4.0*a*c >= 0.0 ){
tp = (-b + sqrt(b*b - 4.0*a*c))/2.0/a;
tm = (-b - sqrt(b*b - 4.0*a*c))/2.0/a;
zp = m + k - m * tp;
zm = m + k - m * tm;
// 2つの解の内、zの値が大きくなるtを選ぶ
if( zp > zm ){
t = tp;
} else {
t = tm;
}
}
float x, y, z; // 交点の座標
// 直線と2次関数の曲面との交点、または直線とz=0平面の交点を算出
x = eye_pos_x + (x_on_paper - eye_pos_x)*t;
y = y_on_paper * t;
z = m + k - m * t;
// 真ん中が空いた四角形上に交点が乗っていないか、確認する。
if (z < 0.0 || y > radius/3.0 || y < -radius * 5.0/3.0
|| ( ( x > -3.0/2.0*radius && x < radius/6.0 ) && ( y > -4.0/3.0*radius && y < 0.0 ) )
){
// 乗っていなければ、直線とz=0平面の交点に置き換える
t = (m+k)/m;
x = eye_pos_x + (x_on_paper - eye_pos_x)*t;
y = y_on_paper * t;
z = m + k - m * t;
}
// 次に、直線と円環が乗る平面(z=circle_pos_z)との交点を算出する
float temp_x, temp_y, temp_z;
t = (m+k-circle_pos_z)/m;
temp_x = eye_pos_x + (x_on_paper - eye_pos_x)*t;
temp_y = y_on_paper * t;
temp_z = m + k - m * t;
// 交点が円環上に乗っているかを確認する
if( (sqrt((temp_x-radius/3.0) * (temp_x-radius/3.0) + (temp_y-radius/3.0) * (temp_y-radius/3.0)) <= 4.0/3.0*radius)
&& (sqrt((temp_x-radius/3.0) * (temp_x-radius/3.0) + (temp_y-radius/3.0) * (temp_y-radius/3.0)) >= 2.0/3.0*radius)
&& (temp_z > z) // 円環上の点がz=0平面、または穴の開いた四角形よりz軸方向で上になっているか
){
// 交点を円環上の交点に更新する
x = temp_x;
y = temp_y;
z = temp_z;
}
PVector result = new PVector(x,y,z);
return result;
}