ここでは、方程式\(z=\cos \sqrt{ x^2+y^2 } \)で表されるバウムクーヘンのような形状の立体図形をランダムドット・ステレオグラムで再現してみたいと思います。なお、この作品は書籍「ステレオグラムをつくろう―あなたも3Dアーティスト」のp.54を参考にしています。
バウムクーヘン
今回、ランダムドット・ステレオグラムで作成する形状は以下のような立体図形となります。
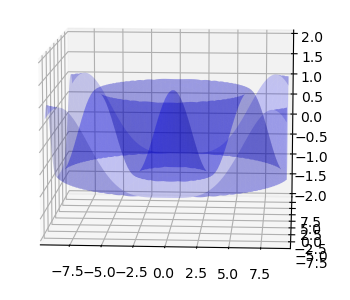
関数で表すと、\(z=A\cos \alpha \sqrt{x^2+y^2} \)となります。
バウムクーヘンのランダムドット・ステレオグラム
今回作成したバウムクーヘン形状のランダムドット・ステレオグラムは次のようになりました。
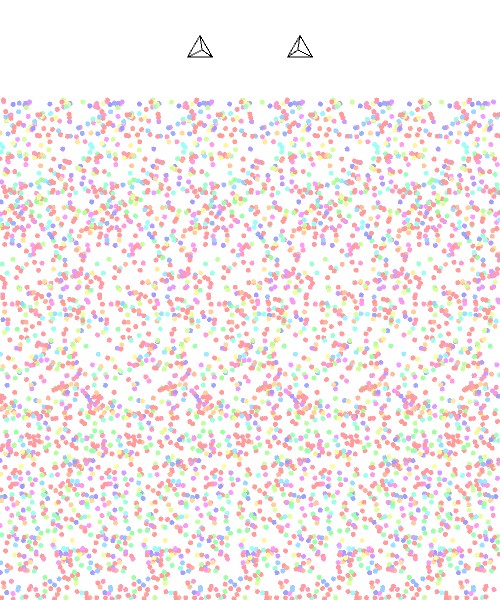
この画像を紙に印刷してじっと眺めてみてください。バウムクーヘンの形状が浮かび上がってくるはずです。ランダムドット・ステレオグラムの見方については、記事「ランダムドット・ステレオグラム」で解説していますので、そちらもご覧ください。
視線と立体との交点の算出
ランダムドット・ステレオグラムの作成方法については、記事「ランダムドット・ステレオグラム」で解説しています。このバウムクーヘンの形状をランダムドット・ステレオグラム化するにあたり一番苦労するところは、やはり目の位置と紙上の点の位置との延長線上に立体との交点を求めるところです。
今回の場合、バウムクーヘンの形状として方程式\(z=A\cos \alpha \sqrt{x^2+y^2} \)が用意されているので、目の位置と紙上の点の位置とを結ぶ直線の方程式\(x=x_E+(x’-x_E)t, \ \ y=y’t, \ \ z=m+k-mt \)を代入して\(t\)についての方程式を解くことで交点の位置を計算することができます。ですが、この\(t\)についての方程式を解析的に解くことはできません。
そのため、今回はこの\(t\)についての方程式をニュートン法を用いて数値的に解くことにしました。ニュートン法については方程式の数値的な解法として初歩的なもので、解説記事もネット検索すればいくつも出てきますので、解説は省略します。
プログラムコード
バウムクーヘンのランダムドット・ステレオグラムを作成したときのプログラムコード(Processing)を載せておきます。
float k = 500.0; // 座標原点から紙までの距離
float m = 500.0; // 紙から目までの距離
float h = 100.0; // 目と目の間の距離の半分
float baumkuchen_size = 100.0; // バウムクーヘンのサイズ
void setup(){
size(500,600,P2D);
background(255,255,255);
PVector point3d; // 立体視したい図形上の点
float x_r, x_l, y_eye; // 紙上の点
float triangular_pyramid_size = 50.0; // 三角錐のサイズ
// 三角錐の4つの頂点のベクトル
PVector triangular_pyramid[] = new PVector[4];
triangular_pyramid[0] = new PVector(0.0, 0.0, sqrt(2.0/3.0)*triangular_pyramid_size);
triangular_pyramid[1] = new PVector(0.0, -1.0/sqrt(3.0)*triangular_pyramid_size, 0.0);
triangular_pyramid[2] = triangular_pyramid[1].copy().rotate(radians(120));
triangular_pyramid[3] = triangular_pyramid[1].copy().rotate(radians(240));
translate(width/2, 50);
// 紙の上に三角錐を左目用と右目用にそれぞれ射影する
for(int i=0; i<4; i++){
for(int j=i+1; j<4; j++){
for(int d=0; d<100; d++){
point3d = triangular_pyramid[i].copy().add(triangular_pyramid[j].copy().sub(triangular_pyramid[i].copy()).mult(d/100.0));
x_r = (m * point3d.x - h * point3d.z + h*k) / (m + k - point3d.z);
x_l = (m * point3d.x + h * point3d.z - h*k) / (m + k - point3d.z);
y_eye = m * point3d.y / (m + k - point3d.z);
point(x_r, y_eye);
point(x_l, y_eye);
}
}
}
translate(0, 300);
float x_ini, y_ini;
for(int i=0; i<1000; i++){
colorMode(HSB);
fill(random(360),100,1000);
noStroke();
x_ini = random(width)-width/2; // 紙上の点の初期値x座標
y_ini = random(width)-width/2; // 紙上の点の初期値y座標
// まず初期値が左目からの座標として処理する
x_l = x_ini;
y_eye = y_ini;
ellipse(x_l, y_eye, 5, 5);
while(true){
// この左目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_l, y_eye, -h);
// この対称物体上の点に対応する、右目からの紙上の座標位置を算出する。
x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
if( abs(x_r) < width/2.0 ){
ellipse(x_r, y_eye, 5, 5);
x_l = x_r;
} else {
break;
}
}
// 次に初期値を右目からの座標として処理する
x_r = x_ini;
while(true){
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_r, y_eye, h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
if( abs(x_l) < width/2.0 ){
ellipse(x_l, y_eye, 5, 5);
x_r = x_l;
} else {
break;
}
}
}
save("stereogram_baumkuchen.jpg");
}
// 対称物体上の点の位置を算出する関数
PVector get3DPoint(
float x_on_paper, // 紙上の点のx座標
float y_on_paper, // 紙上の点のy座標
float eye_pos_x // 左目の場合-h, 右目の場合h
){
float t = (m+k)/m;
float eps = 0.001;
float t_diff = 1.0;
float x, y, z;
// 交点の算出にニュートン法を用いる
while(true){
x = eye_pos_x + (x_on_paper - eye_pos_x)*t;
y = y_on_paper * t;
z = m + k - m * t;
float alpha = 2.0 * PI / width;
float f = baumkuchen_size*cos(alpha * sqrt(x*x+y*y)) - z;
float fx = - baumkuchen_size * alpha * sin(alpha * sqrt(x*x+y*y)) * x / sqrt(x*x+y*y);
float fy = - baumkuchen_size * alpha * sin(alpha * sqrt(x*x+y*y)) * y / sqrt(x*x+y*y);
float fz = -1.0;
float xt = x_on_paper - eye_pos_x;
float yt = y_on_paper;
float zt = -m;
float ft = fx * xt + fy * yt + fz * zt;
t_diff = -f/ft;
t = t + t_diff;
if ( abs(t_diff) < eps ){
break;
}
}
PVector result = new PVector(x,y,z);
return result;
}