ここでは、ボロノイ図について解説します。
ボロノイ図とは
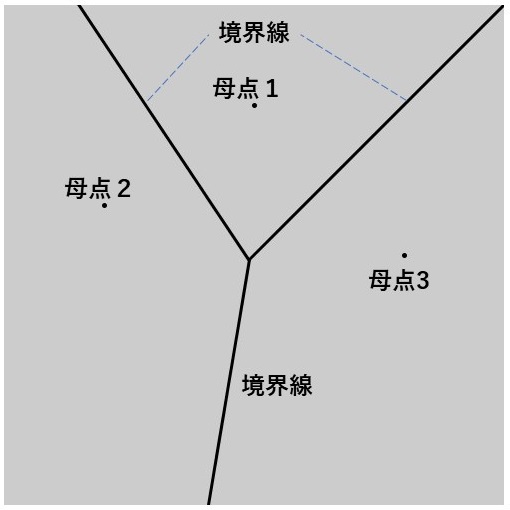
平面上にいくつかの点を打ちます。これらの点を母点と呼びます。次に、平面を母点を一つだけ含む領域に分けていきます。このとき、分割された領域内の任意の点はその領域の母点が他の領域の母点よりも近くなるようにします。このようにして平面上の領域を分割したものをボロノイ図と呼びます。
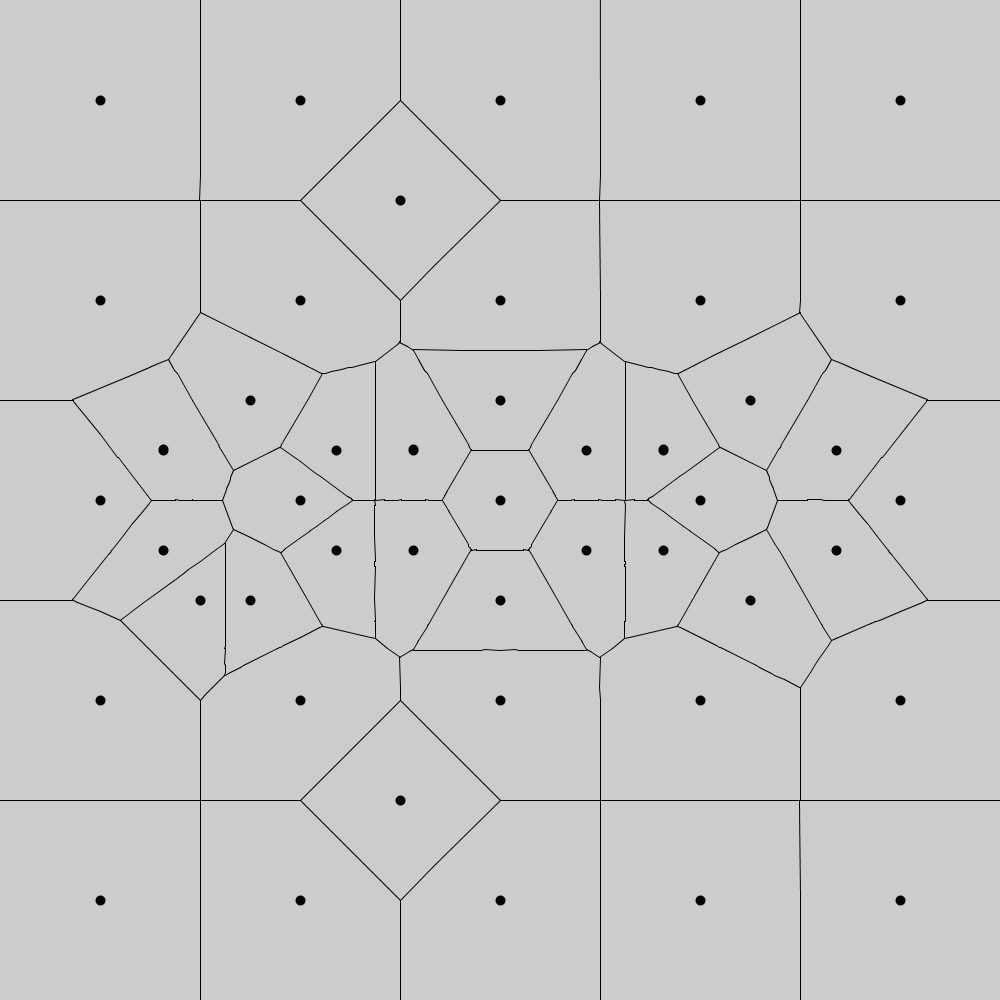
ボロノイ図を作る(Fortune’s Algorithm)
では、これらのボロノイ図を作るプログラムを作成します。
ボロノイ図は、平面上に母点を与えてこれらの母点に近い領域に平面を分割していけばよいので一見簡単そうですが、ちょっと考えるとそう単純ではないことが分かります。
素朴に考えると・・・
2つの母点を結ぶ線分の垂直二等分線を描けば、この線は選ばれた2つの母点から等距離にある点の集合と考えることができますので、ちょうどボロノイ図の境界線となりえます。
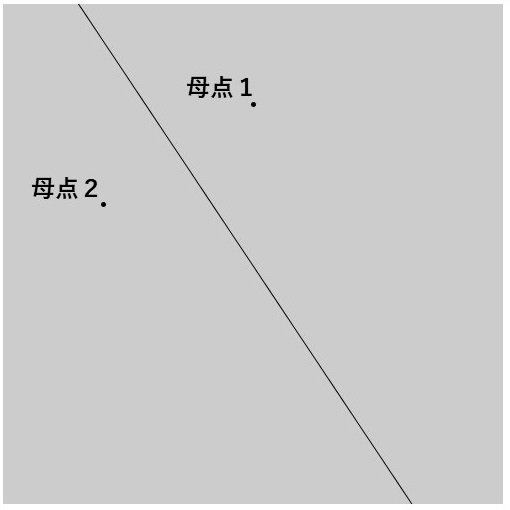
この考え方をもとに3つの母点がある場合での領域分割を考えてみます。3つの垂直二等分線を描くことができ、それらは1つの交点で交わります。
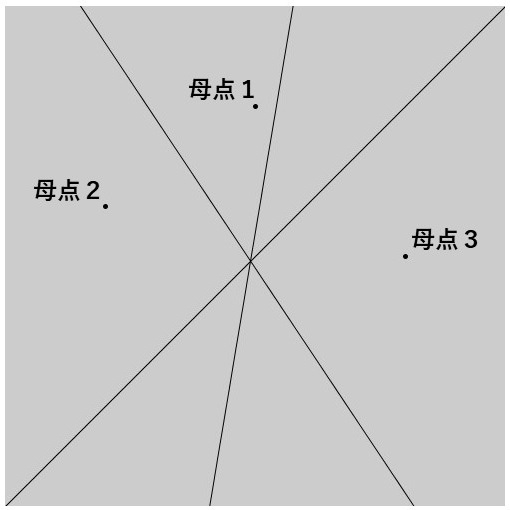
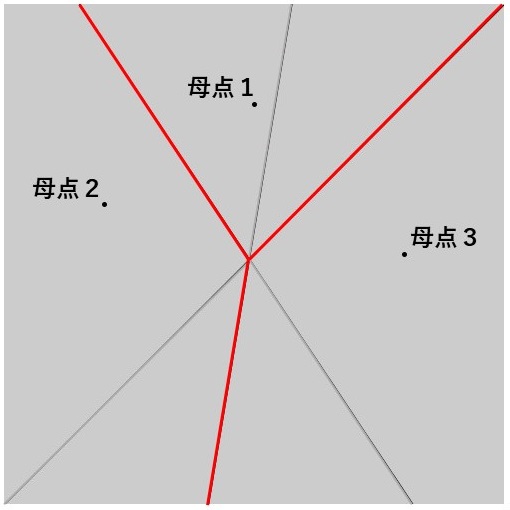
そのため、この交点を求めてそれぞれの垂直二等分線を2つの線分に分けて必要な線分(下図の赤い線分)を選択していくことでボロノイ図を生成することができそうです。ただ、「必要な線分をどう選択していくか」ということは考える必要がありそうです。
では、4つの母点がある場合はどうでしょうか。6つの垂直二等分線を描くことができますが、それぞれの線分の交点は結構複雑になってきますし、交点で分割した線分のうちどれを選んでいけばいいのか、さらによくわからなくなってきます。
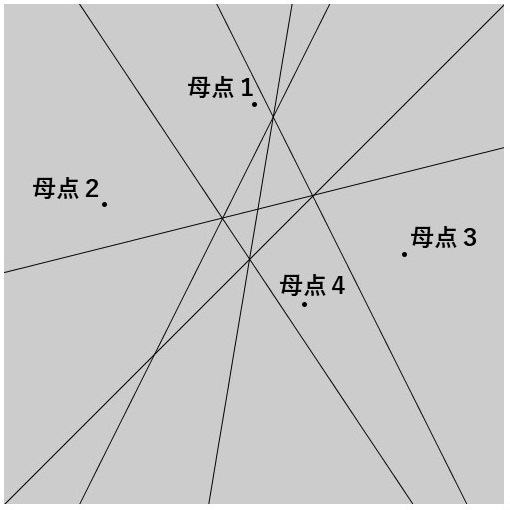
母点が4つ程度であれば、まだ目視で確認することで何とかボロノイ図は作ることができそうです。
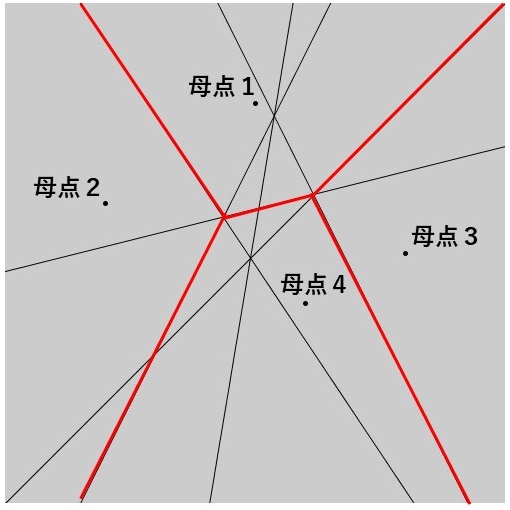
ただ、4つの母点の場合でさえもボロノイ図を作るために必要な線分を選択する処理を考え付くことは結構むずかしそうですし、さらに母点が増えればさらに複雑になることは明らかです。
Fortune’s Algorithm
というわけで、素朴に考えるとちょっと難しそうなボロノイ図の作成ですが、すでにボロノイ図を作る方法はいくつかあるようです。その中で、今回は「Fortune’s Algorithm」を用いた方法でボロノイ図を作りましたので、紹介したいと思います。なお、Ysmr-Ryさんのブログ記事「ボロノイ図を描く! ~Fortune’s Algorithm~ ゆるふわブログ」やこのブログで紹介されている資料を参考にしています。
放物線を利用する
Fortune’s Algorithmの一番のポイントは、ボロノイ図の境界線を求めるために各母点に対応する放物線を利用するところです。ここではまずその放物線について解説します。
「ある定直線\(y=\rho\)(これを準線と呼ぶ)とその直線上にない定点\(F\)(これを焦点と呼ぶ)があるとき、\(y=\rho\)と\(F\)から等距離にある点の軌跡は放物線である」
実際にこの放物線を描いてみると、下記の図のようになります。
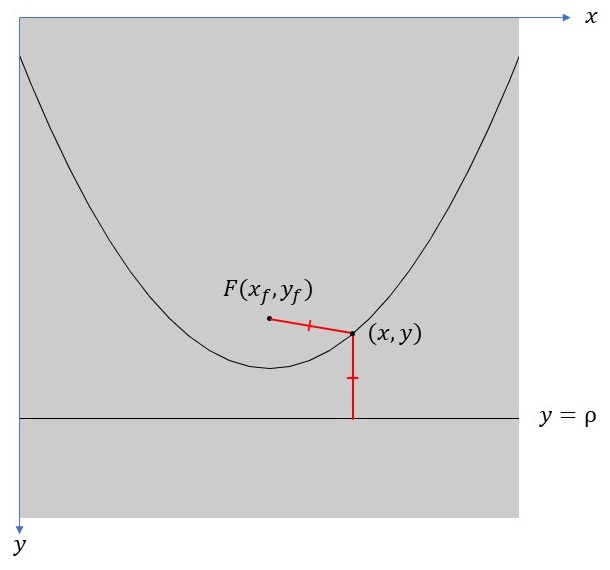
また、焦点\(F\)を\((x_f,y_f)\)とし、この放物線上の点を\((x,y)\)で表すと、放物線の式は、\[ y=-\frac{1}{2(\rho-y_f)}(x-x_f)^2+\frac{\rho+y_f}{2} \]となります。
放物線を利用する利点
母点を焦点とする放物線を2つ描いてみます。ただし、準線は2つの母点よりも下にくるように選びます。すると、2つの放物線は1つまたは2つの交点を持ちます。例えば、下の図のようになります。
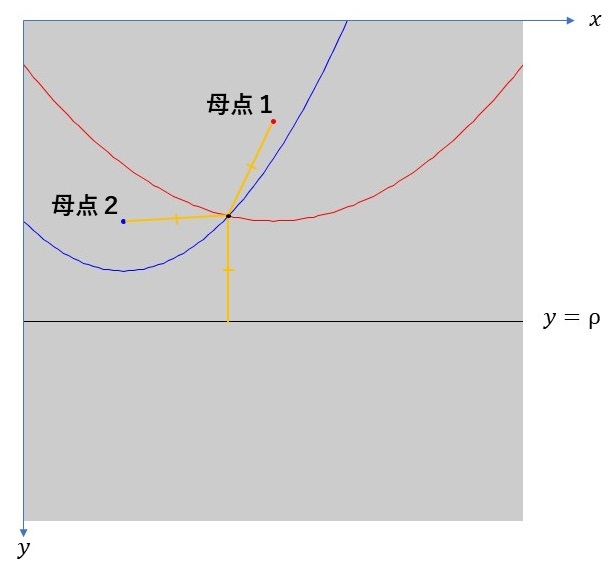
放物線上の点は焦点(ここでは母点)と準線から等距離にあります。したがって、2つの放物線の交点は2つの母点から等距離にあるということができます(2つの放物線の交点は準線からの距離が同じになるからです)。
このことから、準線を変化させていったとき、2つの放物線の交点が描く軌跡は2つの母点から等距離にある点の集合、つまりボロノイ図の境界線になりえるということが分かります。実際、下図に示すように、境界線が描かれます。
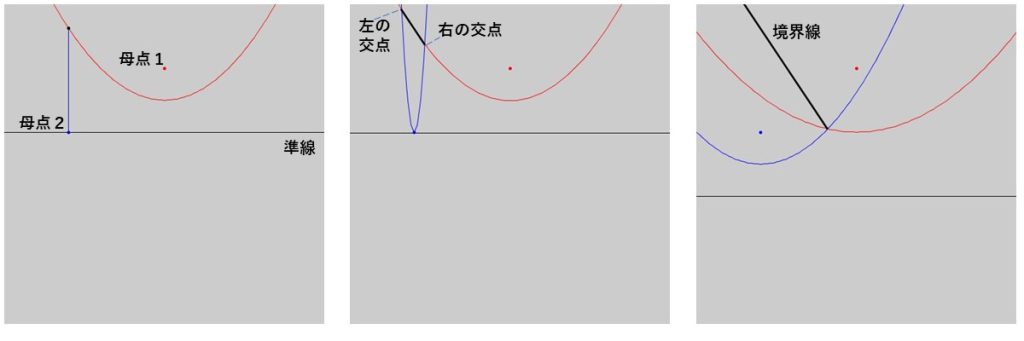
最初準線を母点2を通るところから始めると、母点1の放物線と母点2の放物線の2つの交点(左の交点と右の交点と呼ぶ)が1つに重なった状態で現れます(左図)。準線を下に動かすと左の交点と右の交点が離れる方向に移動していきます(中央図)。さらに準線を下に動かしていくと、左の交点と右の交点がそれぞれ描く軌跡が母点1と母点2の領域の境界線として描かれていきます(右図)。
放物線を利用する利点2
準線を画像の上部(\(y=0\))から始めてだんだん下に下げていくと、準線より上に出てくる母点が増えていきます。このとき、放物線の交点の軌跡を追いかけていくことでボロノイ図の境界線を描くことができます。ただこれだけであれば、垂直二等分線で十分で、放物線を利用しなくてもよさそうです。
放物線を利用する利点の2つ目は、準線より上に母点が3点以上出てくるときに現われてきます。下の図は準線を画像上部から動かして、準線より上に母点が3点出てきたときに3つの放物線の交点の軌跡を追いかけて境界線を描いたものになります。
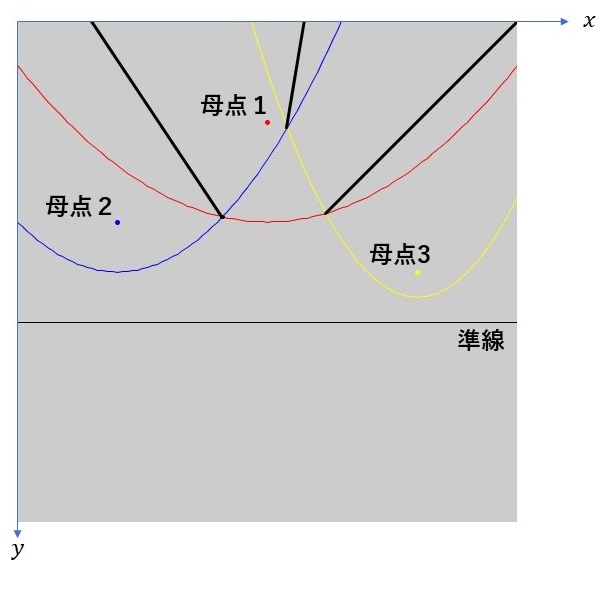
3つの境界線のうち、真ん中の境界線(母点2と母点3の放物線の交点による軌跡)はボロノイ図の境界線ではありません。図で見ても明らかに母点1の領域に入っています。そのため、本来なら描きたくない線です。垂直二等分線で考えたときもこれが問題になりました。
実はこのような余分な境界線は放物線の交点で考えると簡単に除外することができます。下の図のように、各放物線のうち最前線の部分を集めたものを考えます。この線を汀線と呼びます。
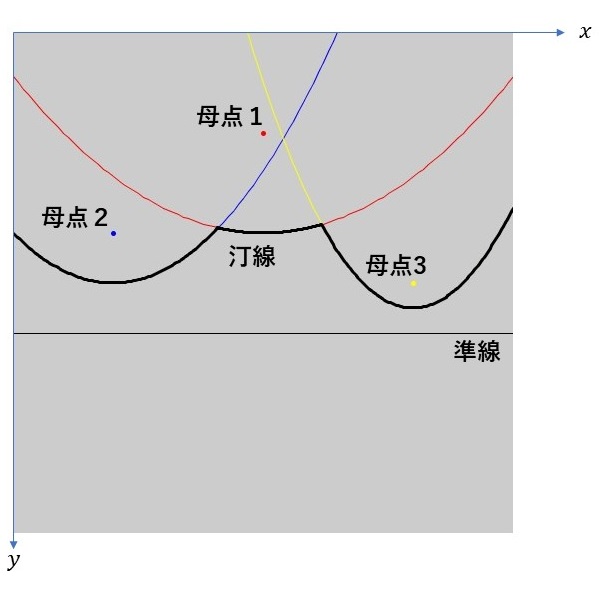
結論からいうと、放物線の交点のうちボロノイ図の境界線として利用するのはこの汀線上に乗っているものだけ、を扱えばよいです。というのも、汀線より上の領域にある点は、いずれかの母点に近い領域に入っているか、ボロノイ図の境界線上の点であるか、のどちらかに決まってしまっているからです(放物線は「準線と焦点から等距離にある点の軌跡」であることを思い出すと、放物線より上にある点は焦点(ここでは母点)に近い点となります)。今回の場合、母点2と母点3による放物線の交点が発生しますが、この交点は汀線より上にあり、すでに他の母点の領域に入っているか、ボロノイ図の境界線上の点になっているかのいずれかに決まっていますので、この交点は無視していいわけです。
汀線上で起こる2つのイベント
ここまででFortune’s Algorithmがだいぶ分かってきました。Fortune’s Algorithmでボロノイ図を作るには、準線を画像の上から下に動かしていったときの汀線上の交点の軌跡を描いていけばいいだけです。
ただ、汀線の交点は準線の移動に伴って変化します。それには以下で示す2つのイベントがかかわっています。
Site Event
1つ目のイベントは「Site Event」です。これは準線を上から下に動かしていった際に準線より上に新たな母点が現れる状況を指します。
母点が準線より上に現われると、新たにその母点に対する放物線が作られます。したがって、汀線上に新たな交点が現れることになります。
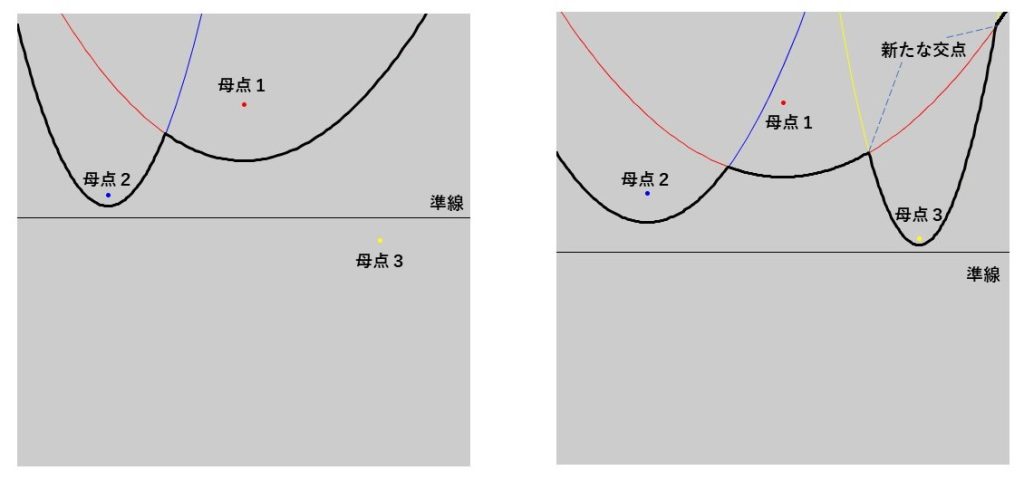
Circle Event
2つ目のイベントは「Circle Event」です。これは準線を上から下に動かしていった際に汀線上の2つ以上の交点が1つに合体したり、逆に1つの交点が2つ以上に分裂したりする状況を指します。
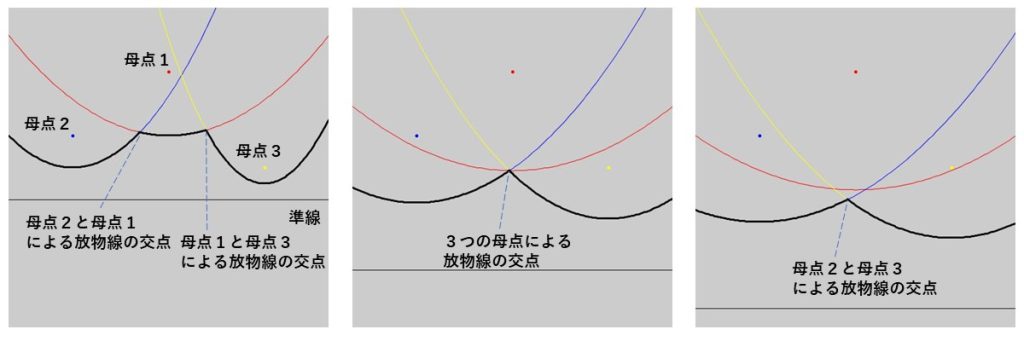
例えば、母点3に関するSite Eventが発生した直後を考えます。このとき、汀線上には母点2と母点1による放物線の交点と母点1と母点3による放物線の交点が乗っています(左図)。準線を下げていくと、これら2つの交点と汀線より上にある母点2と母点3による放物線の交点がだんだん近づいていき、あるタイミングで重なります(中央図)。その後、さらに準線を下げていくと、母点2と母点1による放物線の交点と母点1と母点3による放物線の交点は汀線より上の領域に移動し、代わりに汀線上には、母点2と母点3による放物線の交点が残ります(右図)。Circle Eventはこのような状況を指しています。
汀線上で起こる2つのイベントのタイミング
準線を上から下に下げていったとき、これらのイベントはどういうタイミングで起こるのでしょうか。
まず、Site Eventは簡単です。新たな母点が準線の上に乗ったときです。
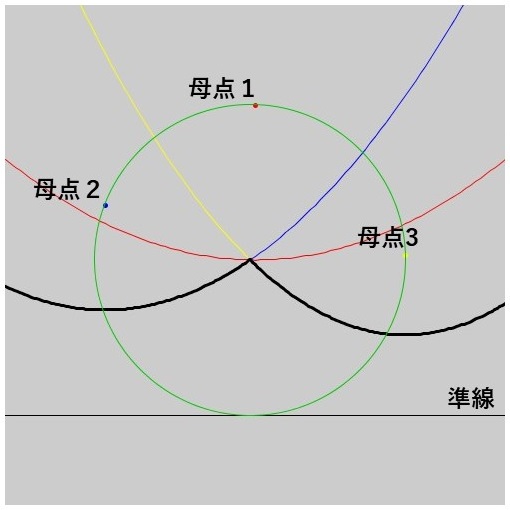
ではCircle Eventはどうでしょうか。上記の例でCircle Eventのポイントは3つの母点による放物線の交点が1点で交わるところでした。Fortune’s Algorithmで扱っている放物線の特徴「準線と焦点から等距離にある点の軌跡」を思い出すと、この交点は3つの母点と準線から等距離にある点であることが分かります。言い換えると、Circle Eventが起こるタイミングは準線が3つの母点を通る円と接するときということができます。これを図で表すと以下のようになります。Circle Eventの名前の由来はこの円から来ています。
汀線上の交点の表し方
ここまででFortune’s Algorithmによるボロノイ図を描くための準備はほぼできました。あとは準線が上から下に移動させていったときの汀線上の交点をうまく管理して、それらの交点の軌跡を描いていけばいいわけです。そのための最後の準備として、汀線上の交点の表し方を決めておきたいと思います。
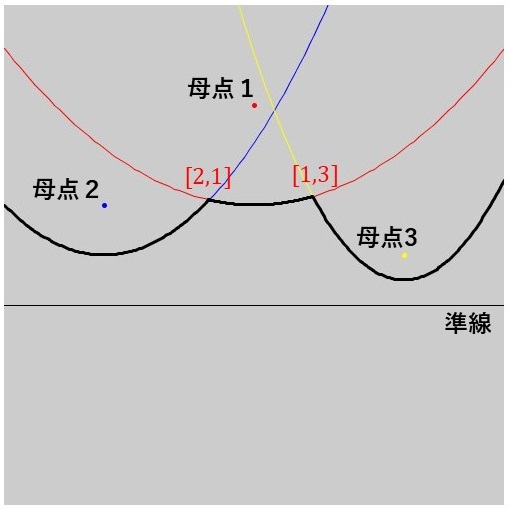
例えば、上の図では汀線上にある2点の交点が示されています。このうち、左側の交点は母点1と母点2の放物線の交点です。この交点に注目して汀線を左から右へ見ていくと、母点2の放物線からこの交点を通り、母点1の放物線に移っていくことが分かります。そこで、この交点を母点の番号を利用して\([2,1]\)と書くことにします。このようなルールで交点を表現すると、もう一つの交点は\([1,3]\)と表すことができます。
まとめると、汀線を左から右へ見て母点\(i\)の放物線から母点\(j\)の放物線へ移るときの交点を\([i,j]\)と表すことにします。
さらに、上図では2つの交点のみ示されていますが、汀線は図の外側にも延びていてその他に2つの交点を持っています。汀線上の交点は左側から順番に並べて
\[ [1,2],[2,1],[1,3],[3,1] \]
と表すことにします。
Fortune’s Algorithmのまとめ
3つの母点がある例で、Fortune’s Algorithmの流れをまとめてます。
① 準線を画像の上部から動かしていきます。準線より上にまだ母点がないので、特に何も起こりません。

② 母点1のSite Event
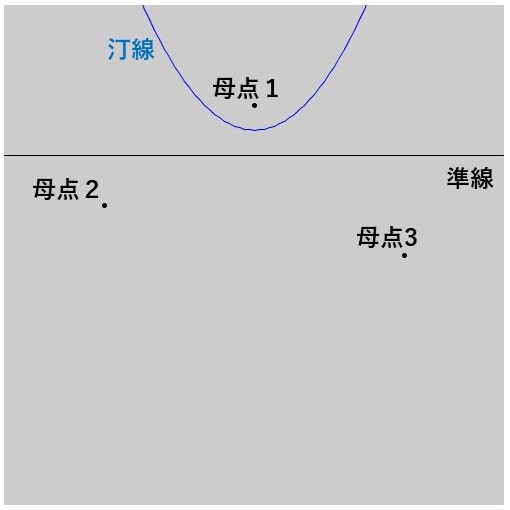
準線を下に動かしていくと、まず母点1のSite Eventが起こります。母点1の放物線が汀線となりますが、まだ汀線上に交点はありませんので、この段階でも特に変化はありません。
③ 母点2のSite Event
次に、母点2のSite Eventが起こります。このとき、はじめて汀線上に交点が出てきます。汀線上の交点は\[ [1,2],[2,1] \]と表すことができます。また、この段階から汀線上の交点の表記に合わせる形でボロノイ図の境界線が描かれ始めます。ここでは母点1の領域と母点2の領域の境界線が描かれ始めています。
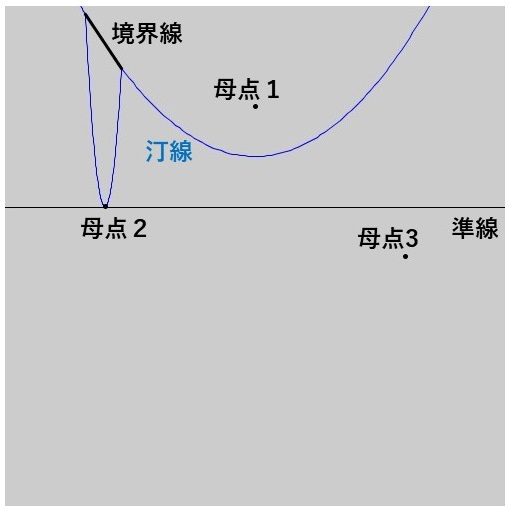
④ 母点3のSite Event
次に、母点3のSite Eventが起こります。このとき、汀線上の交点は\[ [1,2],[2,1] \]から\[ [1,2],[2,1],[1,3],[3,1] \]に変わります。また、この汀線上の交点の変化に合わせて、ボロノイ図での母点1の領域と母点3の領域の境界線も描かれ始めています。
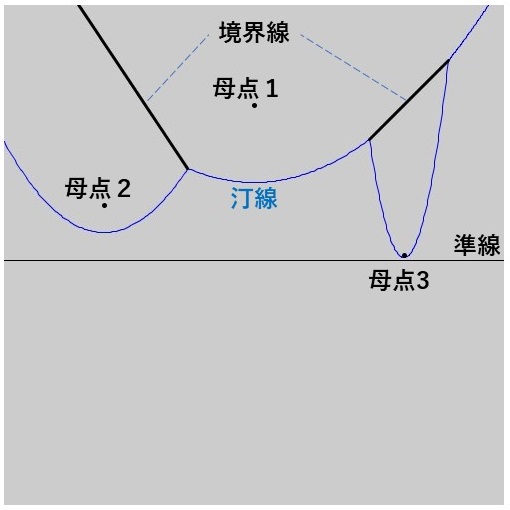
⑤ Circle Event
さらに準線を下げていくと、3つの母点に対してCircle Eventが起こります。このとき、汀線上の交点は\[ [1,2],[2,1],[1,3],[3,1] \]から\[ [1,2],[2,3],[3,1] \]に変わります。この段階で交点\( [2,1] \)と交点\( [1,3] \)による境界線の描画は終り、以後は交点\([2,3]\)による境界線(ボロノイ図での母点1の領域と母点3の領域の境界線)が描かれます。
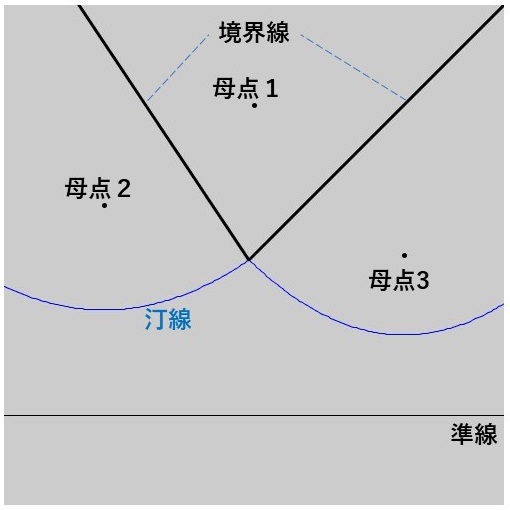
⑥ これ以上準線を下げても、汀線上の交点はこれ以上変わりません。\[ [1,2],[2,3],[3,1] \]の交点の軌跡を描き続けます。
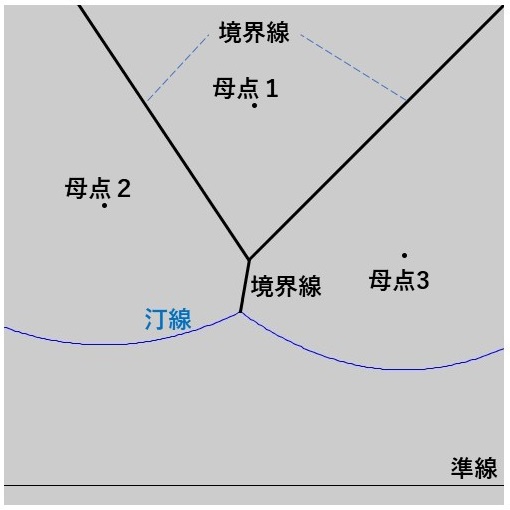
⑦ ボロノイ図完成!
このまま画像範囲を超えて準線を下げ続けていくと、ボロノイ図が完成します。
プログラムコード
今回作成したFortune’s Algorithmによるボロノイ図のプログラムコードを載せておきます。
import java.util.Comparator;
// ボロノイ図を描く
void setup() {
size(500, 500);
// 母点
ArrayList<PVector> generating_points = new ArrayList<PVector>();
generating_points.add(new PVector(250,100));
generating_points.add(new PVector(100,200));
generating_points.add(new PVector(400,250));
drawVoronoiDiagram(generating_points);
save("voronoi_diagram_generating_point_num=3.jpg");
}
// ボロノイ図を描く関数
void drawVoronoiDiagram (
ArrayList<PVector> generating_points
) {
generating_points.add(0, new PVector(width/2.0, -height)); // 母点にダミーの点を入れる
generating_points.add(new PVector(width/2.0, 2.0*height)); // 母点にダミーの点を入れる
// 母点を上から順番に並び変える
generating_points.sort(new CompareToY());
println(generating_points);
// 最後のイベントタイミング(ダミー)を準備する。
float last_event_timing = 2.0*height;
// 汀線上の交点の初期化(ダミーを除く、一番上の母点の位置からスタート)
ArrayList<Integer> intersections = new ArrayList<Integer>();
intersections.add(0);
intersections.add(1);
intersections.add(1);
intersections.add(0);
println(intersections);
// Site Eventが起こるタイミング
ArrayList<Float> site_event_timing = new ArrayList<Float>();
for(int i=0; i<generating_points.size(); i++){
site_event_timing.add(generating_points.get(i).y);
}
site_event_timing.add(last_event_timing); // 最後のタイミング(ダミー)をsite_event_timingの最後に入れておく
int site_event_number = 2; // 次のSite Eventで加えられる母点の番号を表す変数
float present_event_timing = site_event_timing.get(site_event_number); // サイトイベント、サークルイベントを合わせた、現在のイベントのタイミング
float previous_event_timing = site_event_timing.get(site_event_number-1); // // サイトイベント、サークルイベントを合わせた、直前のイベントのタイミング
int event_type = 0; // サイトイベントのとき0、サークルイベントのとき1
int intersection_num = 0;
int next_generating_point_index = 2;
PVector start, end;
PVector[] intersection_pos;
float next_circle_event_timing = last_event_timing;
ArrayList<Integer> exception_index = new ArrayList<Integer>();
while( present_event_timing < last_event_timing ){
println("イベントタイミング:", present_event_timing);
intersection_num = intersections.size()/2; // 汀線上の交点の数
// 前のタイミングと現在のタイミングで交点の位置を取得してそれらの点を結んで境界線を描く
intersection_pos = new PVector[intersection_num];
for(int j=0; j<intersection_num; j++){
int index1 = intersections.get(2*j);
int index2 = intersections.get(2*j+1);
start = getIntersection(generating_points, index1, index2, previous_event_timing);
end = getIntersection(generating_points, index1, index2, present_event_timing);
line(start.x, start.y, end.x, end.y);
intersection_pos[j] = end.copy(); // 交点位置の更新のため、交点位置を保持しておく
}
// intersectionsの更新
if( event_type == 0 ){ // site eventの場合
// 新たに発生する交点の挿入位置を決める
int medial_insert_flag = 0; // 新しく追加される母点のx座標がある交点の位置のx座標が一致する場合1、一致しない場合0
int insert_position = intersection_num;
for(int j=0; j<intersection_num; j++){
if( abs( generating_points.get(next_generating_point_index).x - intersection_pos[j].x ) < 0.001){
insert_position = j;
medial_insert_flag = 1;
exception_index.add(next_generating_point_index);
break;
}
if( generating_points.get(next_generating_point_index).x < intersection_pos[j].x){
insert_position = j;
break;
}
}
// 新たな交点の位置を挿入
if( medial_insert_flag == 1 ){ // 新しく追加される母点のx座標がある交点の位置のx座標が一致する場合
intersections.add(2*insert_position+1, next_generating_point_index);
intersections.add(2*(insert_position+1), next_generating_point_index);
} else if( insert_position == 0 ){ // 挿入位置が一番左側の場合
int outer_index = intersections.get(0);
intersections.add(0, outer_index);
intersections.add(1, next_generating_point_index);
intersections.add(2, next_generating_point_index);
intersections.add(3, outer_index);
} else if( insert_position == intersection_num ){ // 挿入位置が一番右側の場合
int inner_index = intersections.get(2*(insert_position-1)+1);
intersections.add(inner_index);
intersections.add(next_generating_point_index);
intersections.add(next_generating_point_index);
intersections.add(inner_index);
} else { // 挿入位置が配列の位置の間
int inner_index = intersections.get(2*(insert_position-1)+1);
int outer_index = intersections.get(2*insert_position);
intersections.add(2*insert_position, inner_index);
intersections.add(2*insert_position+1, next_generating_point_index);
intersections.add(2*(insert_position+1), next_generating_point_index);
intersections.add(2*(insert_position+1)+1, outer_index);
}
// 次の母点にindexを更新
next_generating_point_index++;
// 汀線上の交点の数を更新
intersection_num++;
} else { // サークルイベントの場合
// 隣り合う交点の位置が重なった場合、交点同士を合体させる
ArrayList<Integer> remove_index = new ArrayList<Integer>();
for(int j=1; j<intersection_num; j++){
if( exception_index.indexOf(intersections.get(2*j)) == -1 && intersections.get(2*j+1) != intersections.get(2*(j-1)) && intersection_pos[j].dist(intersection_pos[j-1]) < 2.0 ){
remove_index.add(j);
}
}
println("除外点:", remove_index);
int remove_num = remove_index.size();
for(int j=remove_num-1; j>=0; j--){
intersections.remove(2*remove_index.get(j));
intersections.remove(2*(remove_index.get(j)-1)+1);
intersection_num--;
}
}
// 次のcircleイベントのタイミングを算出する
next_circle_event_timing = last_event_timing;
for(int j=1; j<intersection_num; j++){
// 3つの母点のindexを取得
int[] circle_point_index = new int[3];
circle_point_index[0] = intersections.get(2*(j-1));
circle_point_index[1] = intersections.get(2*j);
circle_point_index[2] = intersections.get(2*j+1);
// 選択された隣り合った2つの交点のindexが異なる場合計算する
if( circle_point_index[0] != circle_point_index[2] ){
// 選択された3点を通る円の中心と半径を算出する
PVector circle_center;
float circle_radius;
// 関数を挿入
PVector[] circle_point = new PVector[3];
for(int k=0; k<3; k++){
circle_point[k] = generating_points.get(circle_point_index[k]).copy();
}
circle_center = getCercleCenter(circle_point);
circle_radius = circle_point[0].dist(circle_center.copy());
// 「円の中心のy座標+半径」の値が現状のイベントタイミング以上かつ次のサークルイベント発生タイミングより小さい値であれば、
// 次のサークルイベント発生タイミングを「円の中心のy座標+半径」の値に更新する
if( event_type == 0 && exception_index.indexOf(circle_point_index[1]) == -1 && (circle_center.y + circle_radius) > present_event_timing - 0.001 && circle_center.y + circle_radius <= next_circle_event_timing ){
next_circle_event_timing = circle_center.y + circle_radius;
} else if( event_type == 1 && present_event_timing < circle_center.y + circle_radius && circle_center.y + circle_radius < next_circle_event_timing ){
next_circle_event_timing = circle_center.y + circle_radius;
} else {
}
}
}
println("exception:", exception_index);
// 次のタイミングにpresent_event_timingを更新
previous_event_timing = present_event_timing;
if( next_circle_event_timing >= site_event_timing.get(next_generating_point_index) ){
present_event_timing = site_event_timing.get(next_generating_point_index);
event_type = 0;
} else {
present_event_timing = next_circle_event_timing;
event_type = 1;
}
if( abs( present_event_timing - previous_event_timing ) > 0.001 ){
exception_index.clear();
}
println(intersections);
}
// 最後に残った境界線を描く
for(int j=0; j<intersection_num; j++){
int index1 = intersections.get(2*j);
int index2 = intersections.get(2*j+1);
start = getIntersection(generating_points, index1, index2, (float)previous_event_timing);
end = getIntersection(generating_points, index1, index2, (float)present_event_timing);
line(start.x, start.y, end.x, end.y);
}
// 母点を描く
strokeWeight(10);
for(int i=0; i<generating_points.size(); i++){
point(generating_points.get(i).x,generating_points.get(i).y);
}
println("finish");
}
// 母点をそれらのyの値が小さい順でソートするためのクラス
class CompareToY implements Comparator<PVector>
{
//@Override
int compare(PVector v1, PVector v2)
{
return int(v1.y - v2.y);
}
}
// 3つの母点を通る円の中心を求める関数
PVector getCercleCenter(
PVector[] point
){
PVector center = new PVector();
float a = 0.0;
float b = 0.0;
float c = 1.0;
float d = 0.0;
for(int i=0; i<3; i++){
a += point[i%3].x * ( point[(i+1)%3].y - point[(i+2)%3].y );
b += pow(point[i%3].x,2) * ( point[(i+1)%3].y - point[(i+2)%3].y );
c *= point[(i+1)%3].y - point[(i+2)%3].y;
d += point[i%3].x * ( pow(point[(i+1)%3].y,2) - pow(point[(i+2)%3].y,2) ) - point[(i+1)%3].x * point[(i+2)%3].x * (point[(i+1)%3].x - point[(i+2)%3].x);
}
center.x = (b-c)/2.0/a;
center.y = d/2.0/a;
return center;
}
// 与えられた焦点(focus_x,focus_y)と準線y=rhoによる2次関数にxを与えたときのyの値
float quadratic_func(
float x, // 取得したい点のx座標
float focus_x, // 2次関数の焦点のx座標
float focus_y, // 2次関数の焦点のy座標
float rho // 準線の位置
){
float y;
y = - pow(x-focus_x,2)/2.0/(rho-focus_y) + (rho + focus_y)/2.0;
return y;
}
// 左から見て母点index1の放物線と母点index2の放物線が交わる交点の位置を計算する関数
PVector getIntersection (
ArrayList<PVector> generating_points,
int index1, // 左の母点
int index2, // 右の母点
float rho // 準線の位置
){
PVector intersect = new PVector(0.0,0.0);
float x1 = (float) generating_points.get(index1).x;
float y1 = (float) generating_points.get(index1).y;
float x2 = (float) generating_points.get(index2).x;
float y2 = (float) generating_points.get(index2).y;
float a = y2 - y1;
float b = (rho-y1)*x2-(rho-y2)*x1;
float c = (rho-y1)*pow(x2,2)-(rho-y2)*pow(x1,2)+(y1-y2)*(rho-y1)*(rho-y2);
if( abs(y1 - rho) < 0.001 ){
intersect.x = x1;
intersect.y = quadratic_func(intersect.x, x2, y2, rho);
} else if( abs(y2 - rho) < 0.001 ){
intersect.x = x2;
intersect.y = quadratic_func(intersect.x, x1, y1, rho);
} else if( abs(a) < 0.001 ){
intersect.x = c/b/2.0;
intersect.y = quadratic_func(intersect.x, x1, y1, rho);
} else if ( index1 < index2 ){
intersect.x = (b-sqrt(pow(b,2)-a*c))/a;
intersect.y = quadratic_func(intersect.x, x1, y1, rho);
} else {
intersect.x = (b-sqrt(pow(b,2)-a*c))/a;
intersect.y = quadratic_func(intersect.x, x2, y2, rho);
}
return intersect;
}