図形の移動、回転、反転

  1. ホーム
  2. Processingの使い方
  3. 図形の移動、回転、反転

ここでは、図形を移動させたり、回転させたり、反転させたりする方法についてまとめておきます。

※なお、図形の移動、回転、反転に関しては、別記事「図形の移動、回転、反転２」もご覧ください。

図形の移動、回転、反転

図形を描く

まず1000×1000の描画キャンパスに、底辺を400、高さを200とした二等辺三角形を描いてみます。そのときのプログラムコードは以下のようになります。

void setup(){
  size(1000, 1000); // 描画キャンパスを準備
  // 赤色の二等辺三角形を描く
  fill(255,0,0);
  triangle(0.0, 0.0, 200, 200, -200, 200);
}

このプログラムコードを実行させてみると、以下のような図形が描かれます。描画キャンパスの座標系は左上が原点となり、二等辺三角形の頂点の座標を\( (0,0) \)に取っているので、二等辺三角形は半分切れた状態で左上に描かれます。

三角形を描く

図形を移動する

では、図形を移動させてみます。移動はtranslate関数を用いて実行することができます。ここでは二等辺三角形（の頂点）を描画キャンパスの中央に移動させてみました。そのときのプログラムコードは以下です。

void setup(){
  size(1000, 1000); // 描画キャンパスを準備
  // 座標系を描画キャンパスの中央に移動
  translate(width/2, height/2);
  // 赤色の二等辺三角形を描く
  fill(255,0,0);
  triangle(0.0, 0.0, 200, 200, -200, 200);
}

このプログラムコードを実行させてみると、以下のような図形が描かれます。

三角形を中央に移動

確かに、二等辺三角形が中央に移動しました。

何かの図形を描画する場合、最初描画キャンパスの座標系は左上が原点となっていますので、基本的にこのtranslate関数を使って描画キャンパスの方に移動させることが必要になります。

図形を回転させる

次に、図形を回転させてみます。回転はrotate関数を用いて実行することができます。ここでは二等辺三角形（の頂点）を描画キャンパスの中央に移動したあと、時計回りに10度だけ回転させてみました。そのときのプログラムコードは以下です。 

void setup(){
  size(1000, 1000); // 描画キャンパスを準備
  // 座標系を描画キャンパスの中央に移動
  translate(width/2, height/2);
  // 座標系を10°だけ時計回りに回転する
  rotate(radians(10));
  // 赤色の二等辺三角形を描く
  fill(255,0,0);
  triangle(0.0, 0.0, 200, 200, -200, 200);
}

このプログラムコードを実行させてみると、以下のような図形が描かれます。確かに、二等辺三角形が時計回りに10度回転しています。

三角形を時計回りに10度回転

図形を反転させる

最後に、図形を反転させてみます。反転はscale関数を用いて実行することができます。scale関数は図形を横方向や縦方向に伸縮させるための関数ですが、伸縮率をマイナスに設定することで反転させることができます。 ここでは二等辺三角形（の頂点）を描画キャンパスの中央に移動したあと、\(x\)軸回りに反転（上下反転）させてみました。そのときのプログラムコードは以下です。

void setup(){
  size(1000, 1000); // 描画キャンパスを準備
  // 座標系を描画キャンパスの中央に移動
  translate(width/2, height/2);
  // 座標系をx軸回りに反転させる
  scale(1,-1);
  // 赤色の二等辺三角形を描く
  fill(255,0,0);
  triangle(0.0, 0.0, 200, 200, -200, 200);
}

このプログラムコードを実行させてみると、以下のような図形が描かれます。確かに、二等辺三角形が上下反転しています。

三角形を上下反転

図形の移動、回転、反転を組み合わせるときの注意点

図形ではなく座標系が移動、回転、反転する

ここまでは、「図形を移動、回転、反転させる」と書いてきましたが、正確には「座標系を移動、回転、反転させる」というのがより正しい表現になります。実際、上記で紹介したプログラムコードを見てもわかるように、プログラムは、

  1. 座標系を移動、回転、反転させる
  2. 図形をその座標系に合わせて描画する

という順番で記述されていることがわかると思います。「図形を描いてそれを移動、回転、反転させる」わけではないのです。

移動、回転、反転の順番に注意する

あと、座標系を移動、回転、反転させるプログラムコードを書くときはその呼び出しの順番に注意する必要があります。

例えば、上記で実施した「座標系を移動して反転させる」の順番を逆にして「座標系を反転して移動させる」をやってみます。そのときのプログラムコードは以下です。

void setup(){
  // １. 描画キャンパスを準備
  size(1000, 1000); 
  // ２．座標系をx軸回りに反転させる
  scale(1,-1);
  // ３．座標系を描画キャンパスの中央に移動
  translate(width/2, height/2);
  // ４．赤色の二等辺三角形を描画
  fill(255,0,0);
  triangle(0.0, 0.0, 200, 200, -200, 200);
}

このプログラムコードを実行させてみると、以下のようになります。二等辺三角形が消えてしまいます。

二等辺三角形が消える？

なぜこのようなことが起こるかを説明するためにプログラムコードを順にみていきます。

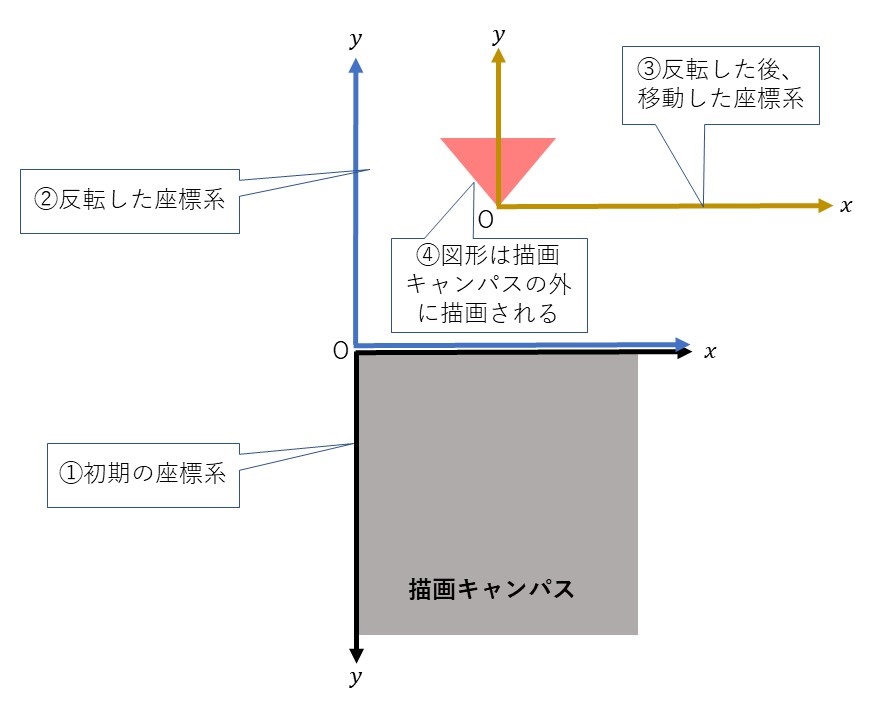
  1. 最初に、描画キャンパスを準備します。このとき、座標系は描画キャンパスの左上を原点とし、右向きを正方向とする\(x\)軸と下向きを正方向とする\(y\)軸を持つものになります。
  2. 次に、scale関数を呼び出して座標系を反転させています。このとき、原点の位置は変わりませんが、\(y\)軸の正方向が下向きから上向きに変わっています。
  3. その後、translate関数を呼び出して座標系を描画キャンパスの中央を表す(width/2,height/2)の位置に移動することを考えていました。ところが、座標系を反転させることで\(y\)軸の正方向が下向きから上向きに変わっていますので、座標系は右下方向（描画キャンパスの中央に向かう方向）ではなく、右上方向に移動します。
  4. 最後に、右上方向に移動した（描画キャンパスから外れてしまった）座標系に合わせて図形を描いてしまったため、図形が描画されないということになってしまいました。
座標系の移動の流れ

以上のことから、座標系の移動、回転、反転を組み合わせて行う際には順番に気を付ける必要があります。つまり、座標系の移動、回転、反転はその処理を実施する直前の座標系を基準に実施されるということに注意が必要です。

コメントを残す