螺旋を描く

  1. ホーム
  2. Processingの使い方
  3. 螺旋を描く

ここでは、processingで螺旋を描くことを考えます。

螺旋の種類

書籍「数学から創るジェネラティブアート」（p.99）によりますと、螺旋には大きく3種類のものがあるようです。拡がりの幅が等間隔のアルキメデス螺旋（下図左）、拡がりの幅が外側に行くにつれて小さくなっていくフェルマー螺旋（下図中央）、そして拡がりの幅が外側に行くにつれて大きくなっていく対数螺旋（下図右）の3つです。

３種類の螺旋

また、各螺旋を数式で表すと以下のようになります。

アルキメデス螺旋：\( x(\theta) = a \theta \cos \theta, \ \ y(\theta) = a \theta \sin \theta \) 、 ただし\(a>0\)

フェルマー螺旋：\( x(\theta) = a \sqrt{\theta} \cos \theta, \ \ y(\theta) = a \sqrt{\theta} \sin \theta \)、 ただし\(a>0\)

対数螺旋： \( x(\theta) = r^{\theta} \cos \theta, \ \ y(\theta) = r^{\theta} \sin \theta \)、 ただし\(r>1\)

螺旋の描画

これらの螺旋を描画する方法としては、上記の式で\(\theta\)を少しずつ変化させながら\((x(\theta), y(\theta))\)をプロットし、それらをつなげていくことで実現できます。以下は上図の螺旋を描いたときのプログラムです。

void setup() {
  // 3種類の螺旋を描く
  size(1000, 300);
  noFill();
  float STEP = 2 * PI * 0.01; // 曲線の精度
  int STEP_num = 1000;

  // アルキメデス螺旋
  translate(width/6.0, height/2.0);
  float theta = 0;
  pushMatrix();
  beginShape();
  for(int i=0; i<STEP_num; i++){
    vertex(2.0 * theta * cos(theta), 2.0 * theta * sin(theta));
    theta += STEP;
  }
  endShape();
  popMatrix();

  // フェルマー螺旋
  translate(width/3.0, 0.0);
  theta = 0;
  pushMatrix();
  beginShape();
  for(int i=0; i<STEP_num; i++){
    vertex(15.0 * sqrt(theta) * cos(theta), 15.0 * sqrt(theta) * sin(theta));
    theta += STEP;
  }
  endShape();
  popMatrix();

  // 対数螺旋
  translate(width/3.0, 0.0);
  float scalar = width/8.0;
  theta = 0;
  pushMatrix();
  beginShape();
  for(int i=0; i<STEP_num; i++){
    vertex(scalar * pow(1.1, theta) * cos(theta), scalar * pow(1.1, theta) * sin(theta));
    theta -= STEP;
  }
  endShape();
  popMatrix();
}

螺旋の回転方向

螺旋の回転方向もポイントです。螺旋は中心から時計回りに広がっていく形状と、中心から反時計回りに広がっていく形状を持ちます。

時計回り（左）と反時計回り（右）の対数螺旋

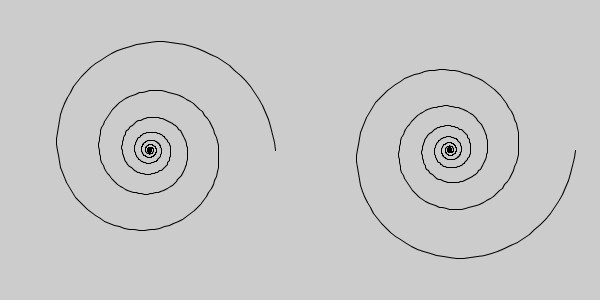
ただ、回転方向の変更はそんなに難しくありません。たとえば、対数螺旋であれば、

\( x(\theta) = r^{\theta} \cos (-\theta), \ \ y(\theta) = r^{\theta} \sin (-\theta) \)

のように、\( \sin, \ \ \cos \)の引数の符号を変えるだけで回転方向を変えることができます。

対数螺旋を描く

線幅が広がっていく対数螺旋

中心から外側に行くにつれて螺旋の幅が広がっていく対数螺旋を描くことを考えます。これは、同じ形状の螺旋を２つ少し角度をずらして描き（左）、その間を塗りつぶす（右）ことで実現できます。

螺旋の幅を考慮して描く

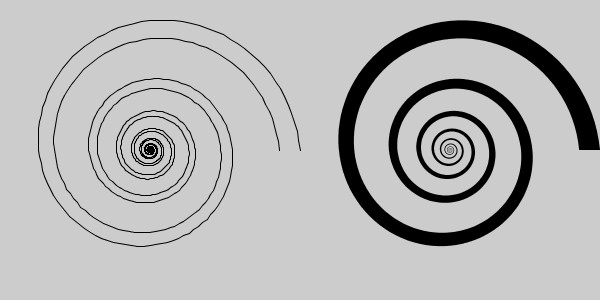
ただし、この方法で螺旋の幅を調整する際にはちょっと注意が必要です。単純に同じ形状の螺旋を2つ少し角度をずらして描くと、ずらす角度の大きさによっては下図のように２つの螺旋の終端位置のずれが影響して塗りつぶしを行ったときに変な形状になってしまいます。

終端位置のずれにより塗りつぶし失敗

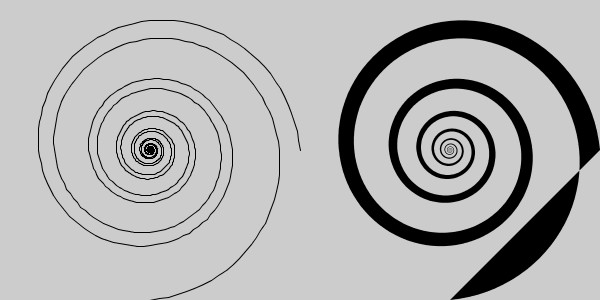
そのため、2つ目に描く螺旋の終端位置については1つ目の終端位置と角度が合うように調整する必要があります。

線幅が広がっていく対数螺旋を描く関数

以上のことを考慮して、この対数螺旋を描くプログラムを関数化しておきます。

void drawLogSpiral(
  float base, // 動径の大きさを定める指数関数の底
  float spiral_width, // 螺旋の幅を決める角度
  float scalar, // 螺旋の最大半径
  float rotate_direction // 回転方向　時計回りの時1.0、反時計回りの時-1.0
  ){
  float STEP = 2 * PI * 0.01; // 曲線の精度
  int STEP_num = 2000;
  float theta = 0;
  pushMatrix();
  beginShape();
  for(int i=0; i<STEP_num; i++){
    vertex(scalar * pow(base, theta) * cos(rotate_direction * theta), scalar * pow(base, theta) * sin(rotate_direction * theta));
    theta -= STEP;
  }
  for(int i=0; i<STEP_num-rotate_direction * spiral_width/STEP; i++){// 終端をそろえるためにステップ数を調整
    theta += STEP;
    vertex(scalar * pow(base, theta) * cos(rotate_direction * theta + spiral_width), scalar * pow(base, theta) * sin(rotate_direction * theta + spiral_width ));
  }
  endShape();
  popMatrix();
}

この関数の使い方としては、以下のようになります。

void setup() {
  size(1000, 1000);

  float spiral_width = radians(90.0); // 螺旋の幅
  float base = 1.1; // 螺旋の動径の大きさを定める指数関数の底
  float rotation_direction = 1.0; // 時計回りの螺旋
 
  translate(width/2.0, height/2.0);
  noStroke();
  fill(0,0,0);
  drawLogSpiral(base, spiral_width, width/2.0, rotation_direction);
}

コメントを残す