円形のグラデーションを描く

  1. ホーム
  2. Processingの使い方
  3. 円形のグラデーションを描く

ある点から外側に向かって色が少しずつ変化しながら広がっていくような図形、つまり、以下の図のような円形のグラデーションの描画を考えます。

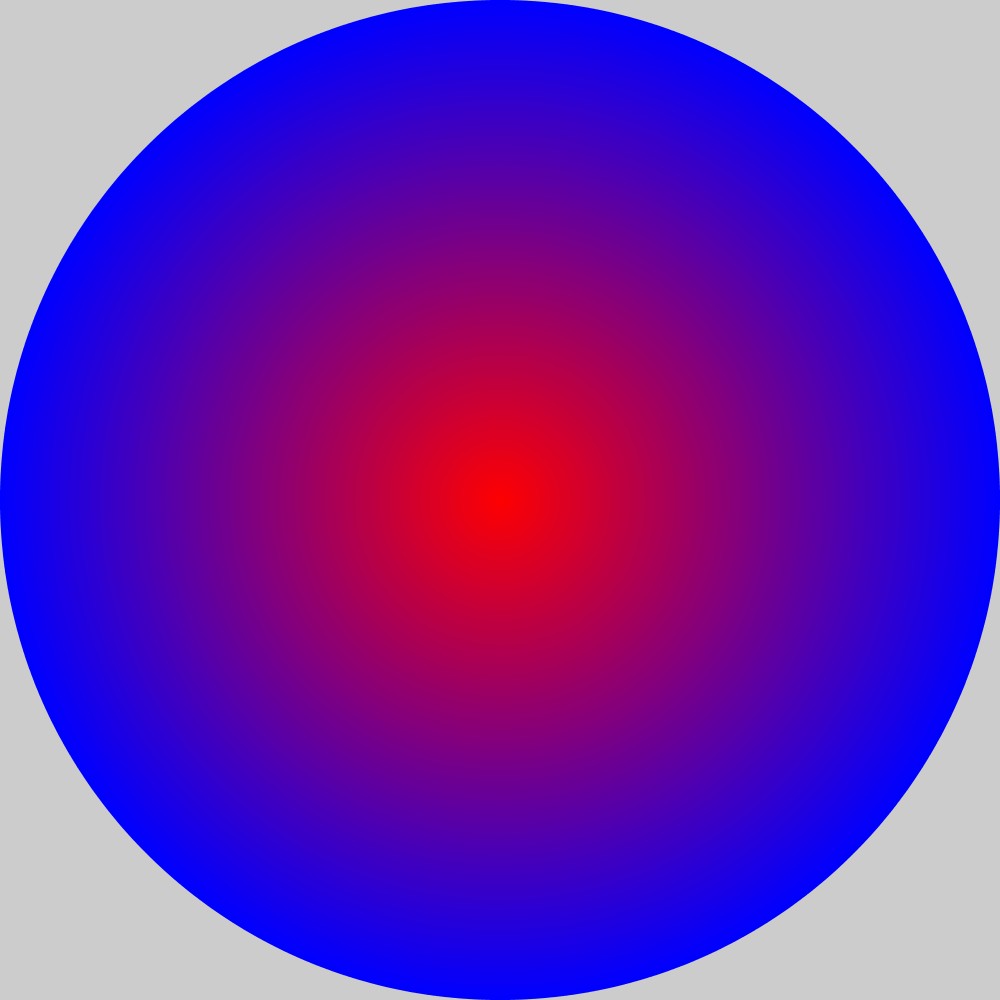
外側から円を重ねていく

円形のグラデーションを描いていくことは、そんなに難しくありません。円の一番外側と一番内側（円の中心部分）の色を決め、まず一番外側の円を描き、次に少し直径を小さくしてかつ色も少し中心側に近づけた円を描く、ということを中心に向かって続けていくことで円形のグラデーションを描くことができます。

円を重ねていくイメージ

「少しずつ小さくする」にはlerp関数を使う

「少し直径を小さくして」と書きましたが、これを実現するためにはlerp関数を使います。「lerp」は線形補間のことです。

lerp(start, stop, amt)

各パラメータは次のようになっています。

  • start　(float)　1つ目の値
  • stop　(float)　2つ目の値
  • amt　(float)　0.0と1.0の間の値

また、返り値は次のようになっています。

  • (float)　(1.0-amt)×start+amt×stop

このlerp関数を使って、次のようなプログラムを書けば、少しずつ小さくなっていく同心円を描くことができます。

void setup() {
  size(1000, 1000);

  float c = 6;
  for (int i=0; i<c; i++) {
    float dd = lerp(width, 0.0, i/c); // 円の直径
    
    noFill();
    ellipse(width/2.0, height/2.0, dd, dd); // 円を描く
  }
}
少しずつ小さくなる同心円

色を変化させるにはlerpColor関数を使う

直径と同じように、色についても変化させることができます。上記のlerp関数を使ってRGBそれぞれを変化させるという方法もあるようですが、色の場合lerpColor関数を使うと便利です。

lerpColor(c1, c2, amt)

各パラメータは次のようになっています。

  • c1　(int)　この色から補間
  • c2　(int)　この色まで補間
  • amt　(float)　0.0と1.0の間の値

また、返り値は次のようになっています。

  • (int)　(1.0-amt)×c1+amt×c2

このlerpColor関数を少しずつ小さくなる同心円と組み合わせることで、円形のグラデーションを描くことができます。

void setup() {
  size(1000, 1000);

  float c = 100;
  for (int i=0; i<c; i++) {
    color col = lerpColor(color(0,0,255), color(255,0,0), i/c); // 円の色
    float dd = lerp(width, 0.0, i/c); // 円の直径
    
    noStroke();
    fill(col);
    ellipse(width/2.0, height/2.0, dd, dd); // 円を描く
  }
}

円形のグラデーションを描く関数

この円形のグラデーションを描くプログラムを関数化しておきます。

void grdCircle(
  float x, // 円の中心位置のx座標
  float y, // 円の中心位置のy座標 
  float d, // 一番外側の円の直径
  color col_out, // 円形のグラデーションの一番外側の色
  color col_in   // 円形のグラデーションの一番内側の色
  ) {
  float c = 100;
  for (int i=0; i<c; i++) {
    color col = lerpColor(col_out, col_in, i/c); // 円の色
    float dd = lerp(d, 0.0, i/c); // 円の直径

    noStroke();
    fill(col);
    ellipse(x, y, dd, dd); // 円を描く
  }
}

この関数の使い方としては、以下のようになります。

void setup() {
  size(1000, 1000);
 
  float diameter = width; // 一番外側の円の直径
  color col_out = color(0,0,255); // 円形のグラデーションの一番外側の色
  color col_in = color(255,0,0); // 円形のグラデーションの一番内側の色
  grdCircle(width/2.0, height/2.0, diameter, col_out, col_in); // 円形のグラデーションを描く
}

コメントを残す