円弧を描く

円弧はarc関数で描く

processingでは、円弧をarc関数で描くことができます。

arc(a, b, c, d, start, stop, mode)

各パラメータは次のようになっています。

• a　(float)　楕円の中心位置のx座標
• b　(float)　楕円の中心位置のy座標
• c　(float)　楕円の幅
• d　(float)　楕円の高さ
• start　(float)　円弧の最初の角度（ラジアン）
• stop　(float)　円弧の終りの角度（ラジアン）
• mode　OPEN、CHORD、PIE、または設定しない

modeにOPENを設定した場合

modeにOPENを設定した場合、円弧と弦で囲まれた部分が塗りつぶされ、円弧部分のみの輪郭が描かれます。

void setup() {
  size(1000, 1000); // ウインドウサイズを幅1000ピクセル、高さ1000ピクセルに指定
  arc(500, 500, 800, 800, -radians(45), radians(45), OPEN);
}

modeにCHORDを設定した場合

modeにCHORDを設定した場合、円弧と弦で囲まれた部分が塗りつぶされ、円弧と弦の輪郭が描かれます。

void setup() {
  size(1000, 1000); // ウインドウサイズを幅1000ピクセル、高さ1000ピクセルに指定
  arc(500, 500, 800, 800, -radians(45), radians(45), CHORD);
}

modeにPIEを設定した場合

modeにPIEを設定した場合、扇形部分が塗りつぶされ、扇形の輪郭が描かれます。

void setup() {
  size(1000, 1000); // ウインドウサイズを幅1000ピクセル、高さ1000ピクセルに指定
  arc(500, 500, 800, 800, -radians(45), radians(45), PIE);
}

modeを設定しない場合

modeを設定しない場合、扇形部分が塗りつぶされ、扇形の円弧部分のみの輪郭が描かれます。

void setup() {
  size(1000, 1000); // ウインドウサイズを幅1000ピクセル、高さ1000ピクセルに指定
  arc(500, 500, 800, 800, -radians(45), radians(45));
}

楕円形の円弧を描く際の注意点

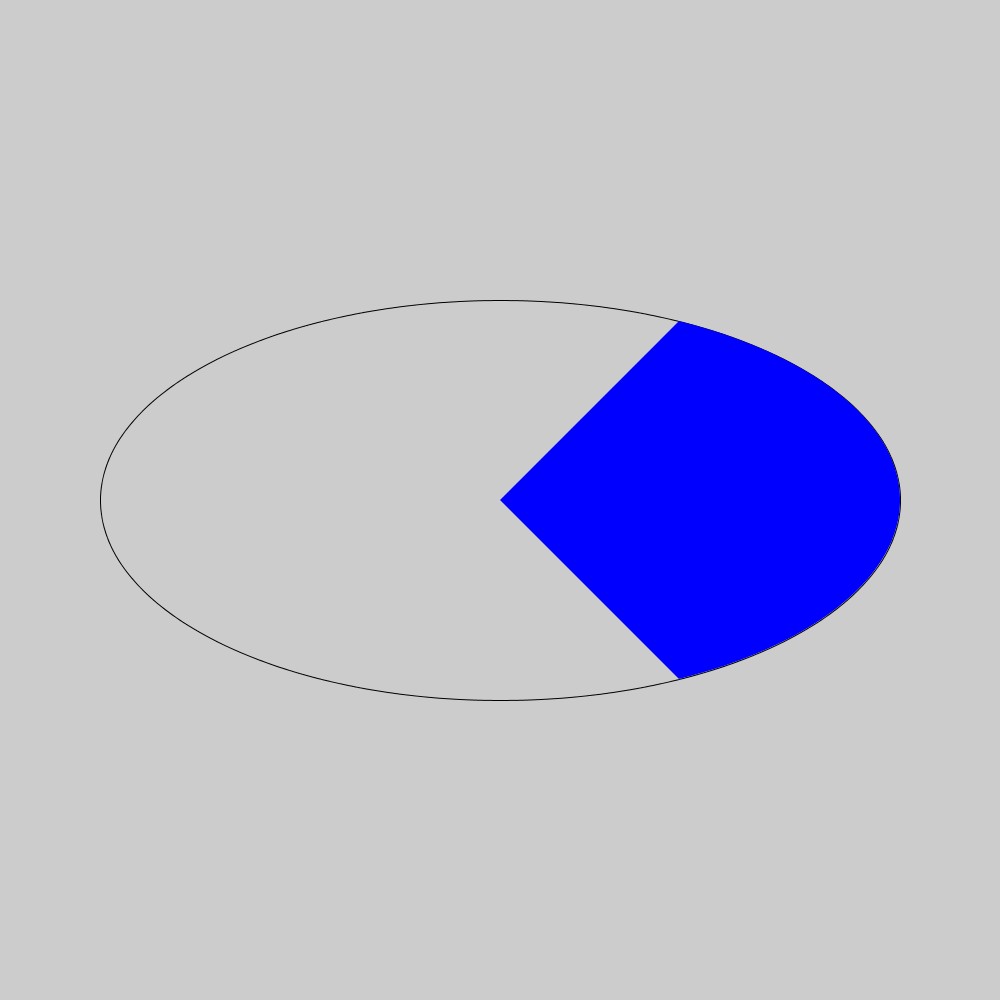
例えば、上図のように楕円形（長軸と短軸の比は2：1）に対して中心角90°で円弧を描くことを考えてみます。単純に考えれば、

arc(500, 500, 800, 400, -radians(45), radians(45));

で描けそうな気がしますが、実際に描いてみると・・・？

明らかに想像していたものと違います。これはどういうことなのでしょうか？

楕円形に対する円弧の実験

明らかに中心角90°に見えない円弧を眺めて、一つ仮説を立ててみました。

楕円形に対する円弧は楕円の長径を直径とする円に対する円弧を短軸方向に短径の長さまでつぶしたものになっているのではないか？

そこで、以下のプログラムを書いて実験してみました。

void setup() {
  size(1000, 1000); // ウインドウサイズを幅1000ピクセル、高さ1000ピクセルに指定

  // 直径800ピクセルの円
  noFill();
  stroke(0,0,0,128);
  ellipse(500,500,800,800);
  
  // 直径800ピクセルの円に対する中心角90°の円弧
  fill(0,255,0,128);
  noStroke();
  arc(500, 500, 800, 800, -radians(45), radians(45)); 
    
  // 幅800ピクセル、高さ400ピクセルの楕円
  noFill();
  stroke(0,0,0,128);
  ellipse(500,500,800,400);
  
  // 幅800ピクセル、高さ400ピクセルの楕円に対する中心角90°の円弧
  fill(255,0,0);
  noStroke();
  arc(500, 500, 800, 400, -radians(45), radians(45));
  
  // 円に対する円弧の端点を結ぶ線
  stroke(0,0,0);
  strokeWeight(2.0);
  line(500+400*cos(radians(45)),500-400*sin(radians(45)),500+400*cos(radians(45)),500+400*sin(radians(45)));
}

つまり、通常の円に対する中心角90°の円弧（緑色）と楕円に対する中心角90°の円弧（赤色）を比較してみます。すると、

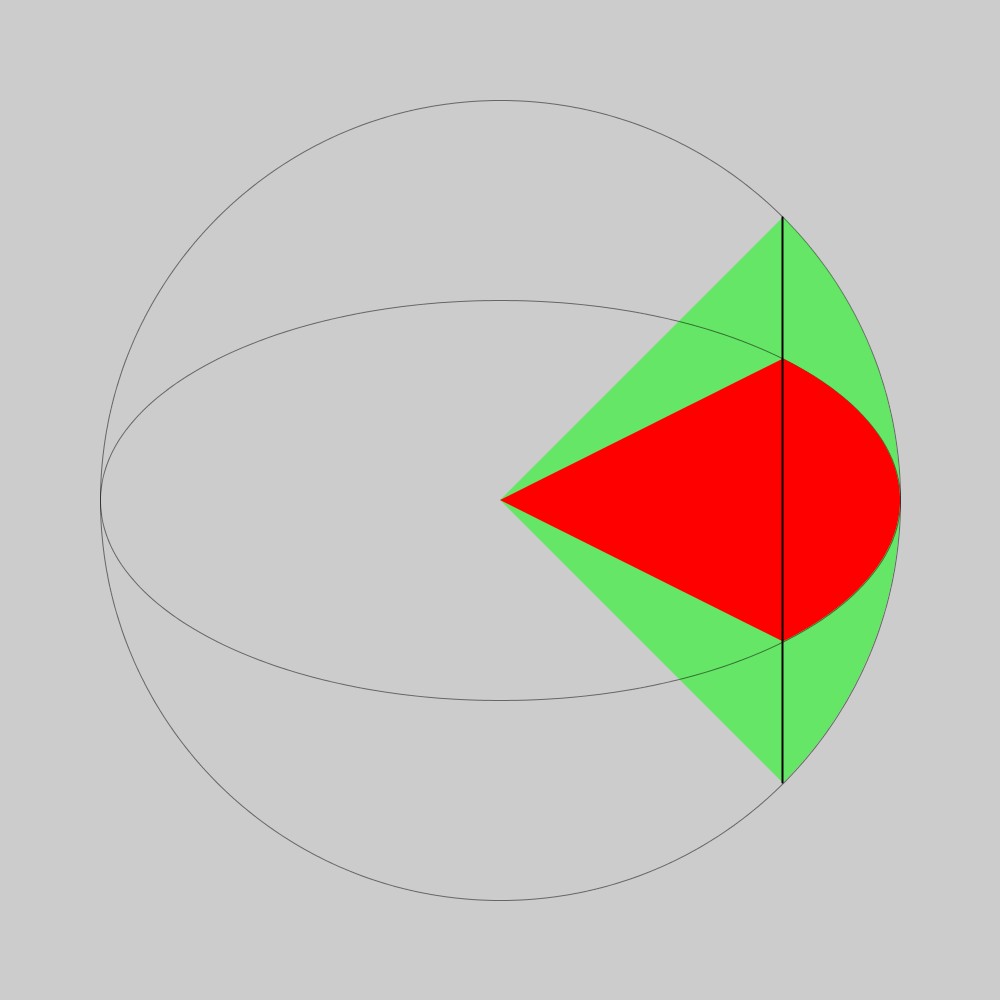
やはり、仮説は正しく、楕円形に対する円弧は楕円の長径を直径とする円に対する円弧を短軸方向に短径の長さまでつぶしたものになっているようです。

楕円形に対する円弧の描き方

この結果から、楕円形に対する中心角90度の円弧の描き方を考えてみます。

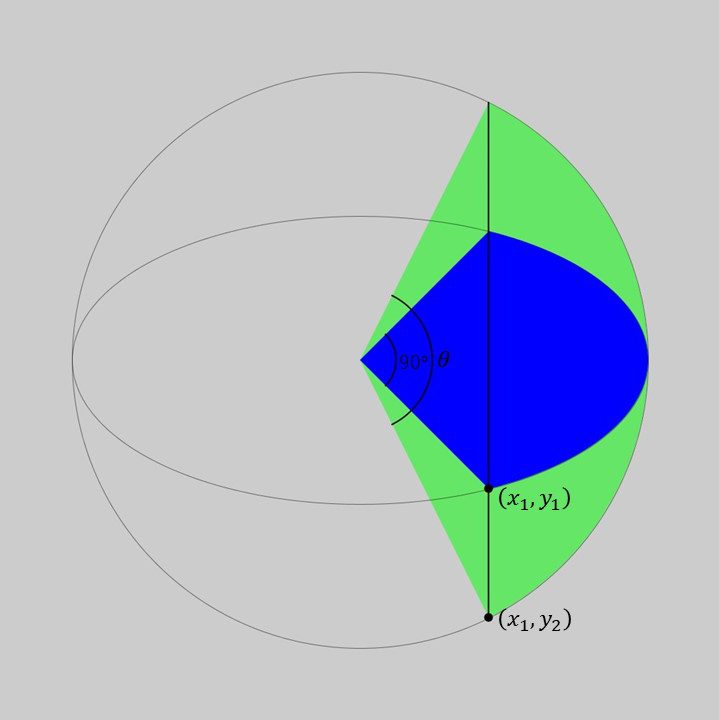
まず、x軸（ここでは長軸方向）に対して45°の方向の線と楕円が交わる点は

\[ (x_1,y_1)=\left( \left[ \frac{\cos^2(45^{\circ})}{a^2}+\frac{\sin^2(45^{\circ})}{b^2} \right]^{-\frac{1}{2}} \cos(45^{\circ}), \left[ \frac{\cos^2(45^{\circ})}{a^2}+\frac{\sin^2(45^{\circ})}{b^2} \right]^{-\frac{1}{2}} \sin(45^{\circ}) \right) \]

となります。ここで、\(2a\)は楕円の長径、\(2b\)は楕円の短径を表します。

次に、楕円の長径を直径とする円上の点で\(x\)座標が\(x_1\)となるような\(y\)座標の値\(y_2\)を求めます。これは、

\[ y_2= \sqrt{a^2-x_1^2} \]

となります。先ほどの実験で楕円の長径を直径とする円に対する円弧を短軸方向に短径の長さまでつぶしたものであることがわかったので、座標\( (x_1,y_2) \)から

\[ \theta = 2 \arctan ( y_2/x_1 ) \]

でつぶす前の円に対する中心角\( \theta \)を求めることができます。

以上から、 楕円形に対する円弧 は

  fill(0,0,255);
  noStroke();
  float x1 = 1.0/sqrt(1.0/pow(400,2)+1.0/pow(200,2));
  float y2 = sqrt(pow(400,2)-pow(x1, 2));
  arc(500, 500, 800, 400, -atan2(y2,x1), atan2(y2,x1));

で描くことができます。

なお、ここでは、

\[ \sin(45^{\circ}) = \cos(45^{\circ}) = \frac{1}{\sqrt{2}} \]

を利用し、また、\( a=400, \ \ b=200 \)としています。