この記事では書籍「世界一美しい錯視アート」に掲載されている「ガンガゼピンク」という作品をProcessingを使って再現してみます。
ガンガゼピンク
今回作成した錯視アート「ガンガゼピンク」は以下です。

書籍「世界一美しい錯視アート」 の表紙にも使われている作品です。
書籍では「ガクガクして見える。」と解説されています。じっと見ていると、確かにガクガク見える気がします。
描き方のポイント
背景はピンクのグラデーション
背景は円形にピンク色でグラデーションしたものになっています。円形のグラデーションは意外に簡単で、円の一番外側と一番内側(円の中心部分)の色を決め、まず一番外側の円を描き、次に少し直径を小さくしてかつ色も少し中心側に近づけた円を描く、ということを中心に向かって続けていくことで円形のグラデーションを描くことができます。詳細は別記事「円形のグラデーションを描く」を見てください。
V字の形状をどう作っていくか
この錯視アートを作っていく上でのポイントはV字の形状をどう作っていくかという点だと思います。今回は以下のように作っていきました。V字の形状は中心に向かうにつれ、だんだん小さくなっていきますが、形状は常に相似になっていると考えられますので、V字同士の対応する各点は一直線上に並ぶと仮定しています。
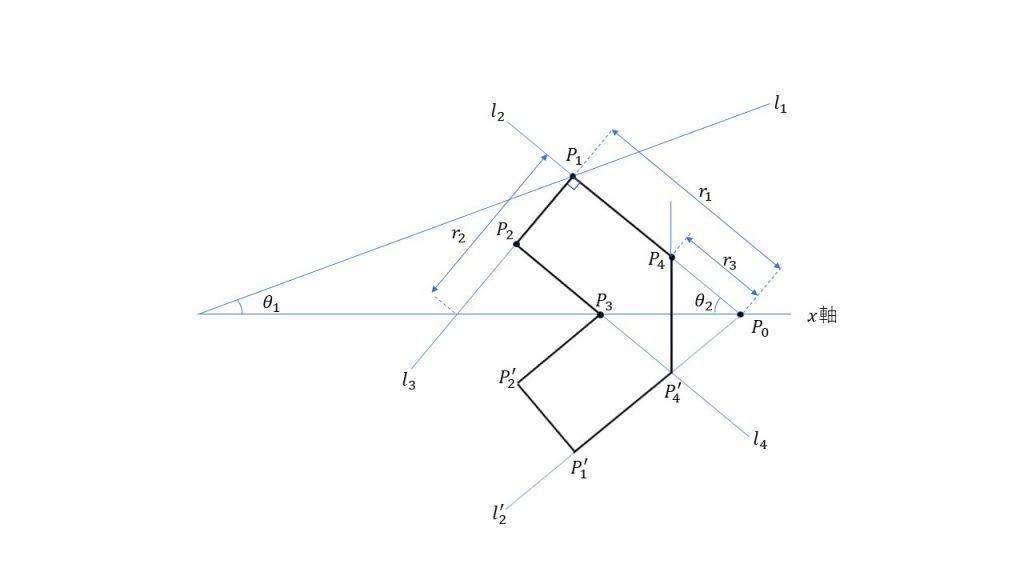
①原点から\(x\)軸の正方向に対して角度\(\theta_1\)となる直線\(l_1\)を考えます。
②\(x\)軸上に点\(P_0(x,0)\)を取り、点\(P_0\)から \(x\)軸の負方向に対して角度\(\theta_2\)となる直線\(l_2\)を考えます。このとき、直線 \(l_1\)と 直線 \(l_2\)が交わる点を\(P_1(x_1,y_1)\)とします。
\[ x_1=x-r_1 \cos \theta_2, \ \ y_1=r_1 \sin \theta_2, \ \ r_1 = \frac{\sin \theta_1}{\sin(\theta_1+\theta_2)} x \]
ここで、\(r_1\)は線分\(P_0P_1\)の長さです。
③点\(P_1\)で直線\(l_2\)と垂直に交わる直線を\(l_3\)とします。そして、点 \(P_1\) と直線 \(l_3\) が \(x\)軸と交わる点の中点を \(P_2(x_2,y_2)\)とします。
\[ x_2 = x_1-\frac{r_2}{2} \sin \theta_2, \ \ y_2=y_1-\frac{r_2}{2} \cos \theta_2, \ \ r_2 = r_1 \tan \theta_2 \]
④点\(P_2\)を通り、直線\(l_2\)と平行な直線を\(l_4\)とします。このとき、この直線\(l_4\)と\(x\)軸が交わる点を\(P_3 (x_3,y_3) \)とします。
\[ x_3 = x-\frac{r_1}{2 \cos \theta_2}, \ \ y_3=0 \]
⑤ \(x\)軸を対称の軸として直線\(l_2\)と線対称な直線を \(l’_2\)とします。また、この直線 \(l’_2\) と直線\(l_4\)が交わる点を\(P’_4\)とします。このとき、 \(x\)軸を対称の軸として点\(P’_4\)と線対称となる点を\(P_4 (x_4,y_4) \)とします。
\[ x_4 = x-r_3 \cos \theta_2, \ \ y_4=r_3 \sin \theta_2, \ \ r_3 = \frac{(x-x_2)\sin \theta_2 – y_2 \cos \theta_2}{\sin 2 \theta_2} \]
⑥最後に、 \(x\)軸を対称の軸として点\(P_1\)及び \(P_2\)と線対称となる点をそれぞれ\(P’_1\)及び \(P’_2\) とします。 これで準備は完了です。後は、点を \(P_1P_2P_3P’_2P’_1P’_4P_4P_1\)の順につないでいけば、ほしい V字の形状 を描くことができます。
⑦点\(P_3\)を点 \(P_0\)として、②から⑥までの手続きを繰り返すことで、原点に向かって、どんどん小さくなっていくV字の形状を描くことができます。
プログラムコード
今回作成した錯視アート「ガンガゼピンク」のプログラムコードを載せておきます。
void setup() {
size(1000, 1000);
translate(width/2, height/2); // 座標の原点を画像の中心位置に移動
color col_out = color(235,110,159); // 背景グラデーションの一番外側の色
color col_in = color(228,0,127); // 背景グラデーションの一番内側の色
grdCircle(0, 0, width*sqrt(2.0), col_out, col_in); // 背景のグラデーションを描く
float th1 = radians(1.0);
float th2 = radians(5.0);
float line_num = 24; // 中心から伸びていく図形の数
for(int i=0; i<line_num; i++){
rotate(radians(360.0/line_num)); // 15°ずつ回転させる
drawVshape(width, th1, th2); // V字の形状を描画
}
save("hatpin_urehin_pink.jpg"); // jpg画像として保存
}
// 円形のグラデーション
void grdCircle(
float x, // 円の中心位置のx座標
float y, // 円の中心位置のy座標
float d, // 一番外側の円の直径
color col_out, // 背景グラデーションの一番外側の色
color col_in // 背景グラデーションの一番内側の色
) {
float c = 100;
for (int i=0; i<c; i++) {
color col = lerpColor(col_out, col_in, i/c); // 円の色
float dd = lerp(d, 0.0, i/c); // 円の直径
noStroke();
fill(col);
ellipse(x, y, dd, dd); // 円を描く
}
}
// V字の形状を作る関数
void drawVshape(
float x, // V字形状を作成する際の基準となるサイズ
float th1, // V字形状を作成する際の基準となるx軸正の方向とのなす角
float th2 // V字形状を作成する際の基準となるx軸負の方向とのなす角
){
int i = 0;
float a = 1.0/2.0;
float r1, r2, r3;
float x1, y1, x2, y2, x3, x4, y4;
while(i<100){
r1 = x * sin(th1) / sin(th1+th2);
x1 = x - r1 * cos(th2);
y1 = r1 * sin(th2);
r2 = r1 * tan(th2);
x2 = x1 - a * r2 * sin(th2);
y2 = y1 - a * r2 * cos(th2);
x3 = x - a * r1 / cos(th2);
r3 = ((x-x2) * sin(th2) - y2 * cos(th2)) / sin(2.0*th2);
x4 = x - r3 * cos(th2);
y4 = r3 * sin(th2);
noStroke();
if (i % 2 == 0){
fill(0,0,0);
} else {
fill(255,255,255);
}
pushMatrix();
beginShape();
vertex(x4,y4);
vertex(x1,y1);
vertex(x2,y2);
vertex(x3,0);
vertex(x2, -y2);
vertex(x1, -y1);
vertex(x4, -y4);
endShape(CLOSE);
popMatrix();
x = x3;
i++;
}
}ガンガゼブルー
書籍「世界一美しい錯視アート」 には、背景がピンクのガンガゼピンクの他、背景がブルーのガンガゼブルーも掲載されていました。それも再現してみました。といっても、背景色を変えただけですが。
