きらめき格子錯視の地球

この記事では書籍「世界一美しい錯視アート」に掲載されている「きらめき格子錯視の地球」という作品をProcessingを使って再現してみます。

Contents

1 きらめき格子錯視の地球
2 描き方のポイント
3 色のきらめき格子錯視の地球

今回作成した錯視アート「きらめき格子錯視の地球」です。

書籍では「ピカピカして見える。」と解説されています。ずっと見ていると眼がちかちかします。

なお、個人的には書籍の作品と少し違うところがあるので、改良の余地があると思っています。

描き方のポイント

描画モードを3D対応にする

この作品は球面を描く必要があります。2Dでもがんばれば描くことができそうですが、Processingでは3Dの図形を描くこともできますので、そちらを使いたいと思います。設定は簡単でsize関数の設定時に、

save(1000,1000,P3D);

と、3番目の引数として「P3D」を入れるだけです。

奥行の位置調整に注意

3Dですので、縦、横の他に奥行をうまく設定することが重要になってきます。その重要さを示す例として、この作品の背景に注目してみます。背景は黒色の下地にグレーの線が縦と横に走っていて、それらの交点に白色の円が描かれています。

グレーの線を描いた後、白色の円を置いていくときのプログラムコードは例えば以下のようになると考えられます。

  noStroke();
  fill(255,255,255);
  for(int i=0; i<10; i++){
    for(int j=0; j<10; j++){  
      float pos_x = width/11.0 * (i + 1);
      float pos_y = height/11.0 * (j + 1);
    
      ellipse(pos_x,pos_y,16*sqrt(2.0),16*sqrt(2.0)); // 円を描く
    }
  }

しかし実際に描いてみると、白色の円が描画されません。

これは、白色の円とグレーの線が奥行方向で同じ位置にあるため、白色の円がグレーの線の中に埋もれてしまったと考えられます。そこで、白色の円を奥行方向に少しだけ前に出すことにします。

  translate(0,0,1); // 3D的に少しだけ前に出す
  noStroke();
  fill(255,255,255);
  for(int i=0; i<10; i++){
    for(int j=0; j<10; j++){  
      float pos_x = width/11.0 * (i + 1);
      float pos_y = height/11.0 * (j + 1);
    
      ellipse(pos_x,pos_y,16*sqrt(2.0),16*sqrt(2.0)); // 円を描く
    }
  }

その結果、白色の円が描画されました。

球面上の座標系について

球面上には、グレーの線と白色の円が描かれています。これらの図形の球面上の位置を示すために、極座標を設定すると便利です。よく使われる3次元の極座標系は以下の図のようなものです。

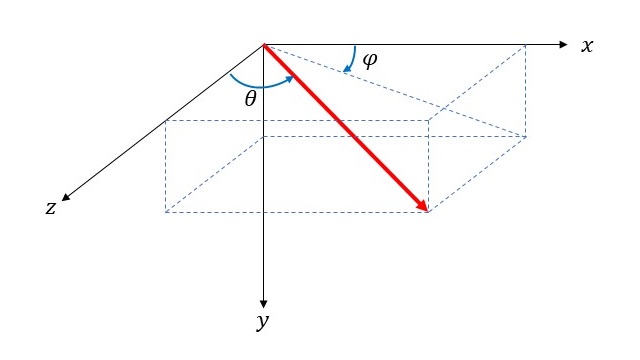
直交座標と極座標の関係を式で表すと、\[ x = r \sin \theta \cos \varphi, \ \ y = r \sin \theta \sin \varphi, \ \ z = r \cos \theta \]となります。

ただ、今回の作品でグレーの線は北極と南極が\(y\)軸上にある球面に対して経度方向と緯度方向が引かれていますので、この極座標系では図形の位置を示しにくいです。そこで、今回の経度と緯度の方向として扱いやすいように少し変更しています。

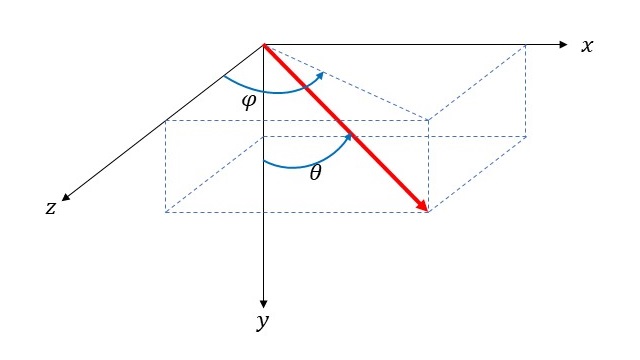
式で書くと、以下のようになります。

\[ x = r \sin \theta \sin \varphi, \ \ y = r \cos \theta, \ \ z = r \sin \theta \cos \varphi \]

単に\(x \to z, \ \ y \to x, \ \ z \to y \)にそれぞれ置き換えたものとなります。

球面上に線を引く

この作品では黒色の球面上にグレーの線を引いています。ただ調べた限り、球面上に張り付く形で線を引くことができる関数などは見つかりませんでした。そこで、今回は小さな長方形を球面上に並べていくことで幅のあるグレーの線を描きました。その時、多少の注意点があります。詳細は以下にまとめています。

球面上に図形を置いていくときの注意

黒色の球面上にグレーの線（小さな長方形）や白色の円を置いていきますが、このときの注意点です。球面上に白色の円を置く場合を例に解説します。

位置を上記の極座標系で計算し白色の円をその位置に置いていきますが、単純に位置だけ指定すると以下の図のように白色の円が正面を向いたままになります。

そのため、白色の円の位置だけでなく、その向きも指定する必要があります。具体的なプログラムコードは以下のようになります。

      translate(cX, cY, cZ);  // 白色の円の位置を決める
      rotateX(radLat-PI/2.0); // 白色の円をx軸周りに回転させる
      rotateY(radLon); // 白色の円をy軸周りに回転させる

白色の円を\(x\)軸や\(y\)軸周りに適切に回転させることで、図形が球面上に張り付いているように描画することができます。

プログラムコード

今回作成した錯視アート「きらめき格子錯視の地球」のプログラムコードを載せておきます。

void setup() {
  size(1000, 1000, P3D);
   
  // 背景を描く
  background(0,0,0); // 黒色背景
  // 背景にグレーのラインを入れる
  stroke(100,100,100);
  for(int i=0; i<10; i++){
    float pos_x = width/11.0 * (i + 1);
    float pos_y = height/11.0 * (i + 1);
    
    strokeWeight(16);
    line(pos_x,0.0,pos_x,height);
    line(0.0,pos_y,width,pos_y);
  }

  // グレーのラインの交点に白色の円を描いていく
  translate(0,0,1); // 3D的に少しだけ前に出す
  noStroke();
  fill(255,255,255);
  for(int i=0; i<10; i++){
    for(int j=0; j<10; j++){  
      float pos_x = width/11.0 * (i + 1);
      float pos_y = height/11.0 * (j + 1);
    
      ellipse(pos_x,pos_y,16*sqrt(2.0),16*sqrt(2.0));
    }
  }
  
  // 球体を描いていく
  translate(width/2.0, height/2.0, -width*0.15);
  
  // まず、黒色の球体を描く
  float radius = width/2.0;
  noStroke();
  fill(0,0,0);
  sphere(radius);

  // 経度方向にグレーの線を引いていく
  // 線は小さな矩形を並べていくことで表現している
  float divLat = 0.1;
  float divLon = 360/30;
  for (float lon = -divLon*6; lon <= divLon*5; lon += divLon) {
    float radLon = radians(lon)+radians(divLon/2.0);
  
    for (float lat = 0.0; lat <= 180.0; lat += divLat) {
      float radLat = radians(lat);

      float cX = radius * sin(radLon) * sin(radLat);
      float cY = radius * cos(radLat);
      float cZ = radius * cos(radLon) * sin(radLat);

      pushMatrix();
      // 座標は translate で設定 
      translate(cX, cY, cZ);
      rotateX(radLat-PI/2.0);
      rotateY(radLon);

      fill(100,100,100);
      rectMode(CENTER);
      rect(0,0,16,10);
      popMatrix();
    }
  }
  
  // 緯度方向にグレーの線を引いていく
  // 線は小さな矩形を並べていくことで表現している
  divLat = 360/30;
  divLon = 0.1;
  for (float lat = 0.0; lat <= 180.0; lat += divLat) {
    float radLat = radians(lat);
    // 経度
    for (float lon = -90.0; lon <=90.0 ; lon += divLon) {
      float radLon = radians(lon);
  
      float cX = radius * sin(radLon) * sin(radLat);
      float cY = radius * cos(radLat);
      float cZ = radius * cos(radLon) * sin(radLat);

      pushMatrix();
      // 座標は translate で設定 
      translate(cX, cY, cZ);
      rotateX(radLat-PI/2.0);
      rotateY(radLon);

      fill(100,100,100);
      rectMode(CENTER);
      rect(0,0,10,16);
      popMatrix();
    }
  }
  
  // グレーの経線、緯線の交点に白色の円を置いていく
  divLat = 360/30;
  divLon = 360/30;
  float delta_r = 2.0; // 球面の表面から少しだけ浮かす
  // 経度
  for (float lon = -divLon*6; lon <= divLon*5; lon += divLon) {
    float radLon = radians(lon)+radians(divLon/2.0);
    // 緯度
    for (float lat = 0.0; lat <= 180.0; lat += divLat) {
      float radLat = radians(lat);

      float cX = (radius+delta_r) * sin(radLon) * sin(radLat);
      float cY = (radius+delta_r) * cos(radLat);
      float cZ = (radius+delta_r) * cos(radLon) * sin(radLat);

      pushMatrix();
      // 座標は translate で設定 
      translate(cX, cY, cZ);
      rotateX(radLat-PI/2.0);
      rotateY(radLon);

      fill(255,255,255);
      rectMode(CENTER);
      ellipse(0,0,16*sqrt(2.0),16*sqrt(2.0));
      popMatrix();
    }
  }
}

色のきらめき格子錯視の地球

書籍「世界一美しい錯視アート」には、黒色とグレーの代わりに青色と緑色が使われた「色のきらめき格子錯視の地球」も掲載されていましたので、それも再現してみました。