眼光 - 数学アートの部屋

この記事では書籍「世界一美しい錯視アート」に掲載されている「眼光」という作品をProcessingを使って再現してみます。

Contents

1 眼光
2 描き方のポイント
3 おまけ

眼光

今回作成した錯視アート「眼光」です。

書籍では「放射状パターンが拡大して見えるとともに、ガクガクして見える。」と解説されています。自分にもそのように見えます。気持ち悪くなるくらいに。

描き方のポイント

放射線上に三日月型の図形を並べていく

この作品では、キャンバスの中心から楕円状の図形が少しずつ大きくなりながら動径方向に拡がっていくものが18本出ています。そこで最初、別記事「縮小していく線分を描く」で紹介した方法を用いて楕円を並べていくことで作品を再現してみましたが、あまりしっくりこなかったので、ベジエ曲線を用いて三日月型の図形を作成し、それを並べていくことにしました。

三日月型図形の作成

三日月型の図形はベジエ曲線を用いて作成しています。今回のベジエ曲線は次のようにして描いています。ベジエ曲線の始点を\((x,y)\)、終点を\((x,-y)\)のよう\(x\)軸周りに対称となるようにとります。次にベジエ曲線の2つの制御点を\((x-r,\frac{3}{4}y)\)、 \((x-r,-\frac{3}{4}y)\)ととります。\(r\)は制御点を調整するパラメータで、描いてみながら調整しました。このパラメータ設定で3次のベジエ曲線を描くと以下の図のような曲線が得られます。

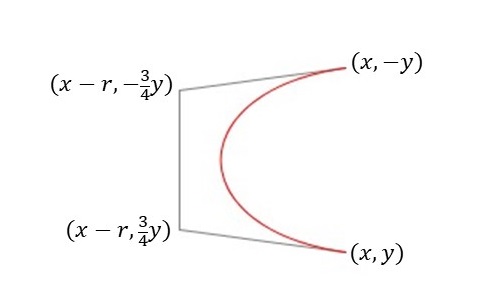
このようなベジエ曲線を2つ用意してそれらの始点同士、終点同士を線分で結ぶことで、以下の図のような三日月型の図形を作成することができます。

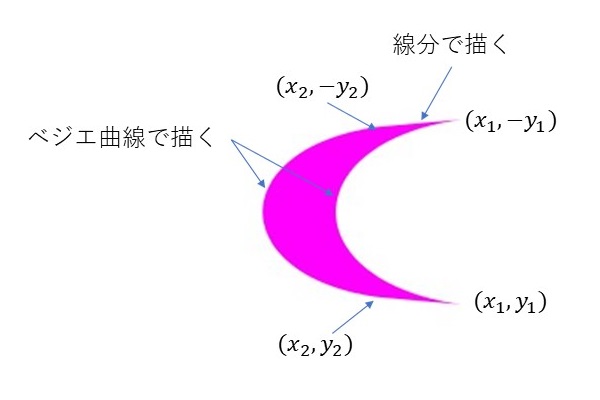
なお、上記の図の\(x_1, \ \ y_1, \ \ x_2, \ \ y_2\)の関係は、別記事「縮小していく線分を描く」で紹介した方法で算出される縮小比率\(r\)を用いると、

\[ x_2 = x_1 \times r, \ \ y_2 = y_1 \times r \]

となっています。

中央の眼もベジエ曲線を用いて再現

中央にある眼のような形の図形も最初楕円で表現しようと思いましたが、よく見ると眼の端の方が少し尖ったような形をしていましたので、こちらもベジエ曲線を用いて再現しました。

プログラムコード

今回作成した錯視アート「眼光」のプログラムコードを載せておきます。

void setup() {   
  size(1000, 1000);
  
  noStroke();
  translate(width/2, height/2);
  
  color col_out = color(#FF0320); // 円形のグラデーションの一番外側の色
  color col_in = color(#FF95A2); // 円形のグラデーションの一番内側の色  
  grdCircle(0.0, 0.0, sqrt(2.0)*width, col_out, col_in); // 円形のグラデーションを描く
  
  float line_len = sqrt(2.0)*width/2.0; // 三日月型図形列の収束点からの距離の初期値）
  float anckor_point_initial = width/9.0; // ベジエ曲線を描く際の制御点を調整するための値の初期値
  float segment_len_initial = width/18.0; // 三日月型図形の大きさの初期値
  float ratio = 1.0 - segment_len_initial / line_len; // 縮小比率
  
  int line_num = 18; // 中心から伸びていく図形の数
  float th1 =  radians(360.0/line_num/2.0); // 中心での角度
  rotate(-th1);
  for(int i=0; i<line_num; i++){
    rotate(2.0*th1);  
    drawCrescentMoon(line_len, anckor_point_initial, segment_len_initial, ratio, th1);
  }
  rotate(th1); 

  // 中心の眼の形を描画
  drawEye();
}

// 円形のグラデーションを描く関数
void grdCircle(
  float x, // 円の中心位置のx座標
  float y, // 円の中心位置のy座標 
  float d, // 一番外側の円の直径
  color col_out, // 円形のグラデーションの一番外側の色
  color col_in   // 円形のグラデーションの一番内側の色
  ) {
  float c = 100;
  for (int i=0; i<c; i++) {
    color col = lerpColor(col_out, col_in, i/c); // 円の色
    float dd = lerp(d, 0.0, i/c); // 円の直径

    noStroke();
    fill(col);
    ellipse(x, y, dd, dd); // 円を描く
  }
}

// ベジエ曲線で作った三日月型の図形を縮小させながら並べていく関数
void drawCrescentMoon(
  float line_len, // 線全体の長さ（収束点からの長さの初期値）
  float anchor_point_initial, // ベジエ曲線の制御点の位置に関する初期値
  float segment_len_initial, // 線分の長さの初期値
  float ratio, // 縮小比率
  float theta // 収束点での角度
){
  float c;
  color col_out, col_in;
  float[] x = new float[100];
  float[] y = new float[100];
  float[] r = new float[100]; 

  // 三日月型図形を収束点からの長さの初期値よりもう1つ外側に作成する
  c = segment_len_initial / ratio;
  x[0] = line_len * cos(theta/2.0) + c;
  y[0] = line_len * sin(theta/2.0) / ratio;  
  r[0] = anchor_point_initial / ratio;

  // 三日月型図形を並べていく準備
  int i = 0;
  while(i<99){
    i++;
    x[i] = x[i-1] - c;
    y[i] = y[i-1] * ratio;
    r[i] = r[i-1] * ratio;
    c = c * ratio;
  }

  // 収束点の方から三日月型図形を並べていく
  i=0;
  while(i<100-1){
    
    noStroke();
    // 偶数番目と奇数番目で色を変える
    if (i % 2 == 0){
      col_out = color(#90003F);
      col_in = color(#FF0370);
    } else {
      col_out = color(#FAFF00);
      col_in = color(#C8CB00);
    }
    // 三日月型の図形を描く
    grdCrescentMoon(x[99-i], y[99-i], r[99-i], x[98-i], y[98-i], r[98-i], col_out, col_in);
    i++;
  }
}

// 三日月型の図形を描く関数
void grdCrescentMoon(
  float x1, // 三日月型の外側に来るベジエ曲線の頂点のx座標
  float y1, // 三日月型の外側に来るベジエ曲線の頂点のy座標
  float r1, // 三日月型の外側に来るベジエ曲線の制御点を調整するための距離
  float x2, // 三日月型の内側に来るベジエ曲線の頂点のx座標
  float y2, // 三日月型の内側に来るベジエ曲線の頂点のy座標
  float r2, // 三日月型の内側に来るベジエ曲線の制御点を調整するための距離
  color col_out, // グラデーションの外側の色
  color col_in // グラデーションの内側の色
){
  
  float diff_x = x2-x1;
  float diff_y = y2-y1;

  // 三日月型の図形を少しずつ小さくし、色を変化させながら描くことでグラデーションさせる
  float c = 100;
  for (int i=0; i<c; i++) {
    color col = lerpColor(col_out, col_in, i/c);
    float dd_x = lerp(0.0, diff_x, i/c);
    float dd_y = lerp(0.0, diff_y, i/c);
    float dd_r = lerp(x1-r1, x2-r2, i/c);

    // 三日月型の図形を描く
    noStroke();
    fill(col);
    beginShape();
    vertex(x1+dd_x,y1+dd_y);
    bezierVertex(dd_r, (y1+dd_y)*3.0/4.0, dd_r, -(y1+dd_y)*3.0/4.0, x1+dd_x,-(y1+dd_y));
    vertex(x2, -y2);
    bezierVertex(x2-r2, -y2*3.0/4.0, x2-r2, y2*3.0/4.0, x2, y2);
    endShape(CLOSE);
  }
}

// 中央にある眼のような形を描く関数
void drawEye(){
  float w, h;
  w = width / 25.0;
  h = width / 70.0;
  
  stroke(0,0,0);
  beginShape();
  vertex(-w/2.0,-h/10.0);
  bezierVertex(-w/6.0, -h*11.0/10.0, w/6.0, -h*11.0/10.0, w/2.0, -h/10.0);
  endShape();
  stroke(0,0,0);
  beginShape();
  vertex(w/2.0, h/10.0);
  bezierVertex(w/6.0, h*11.0/10.0, -w/6.0, h*11.0/10.0, -w/2.0, h/10.0);
  endShape();
  
  noStroke();
  fill(255,255,255);
  beginShape();
  vertex(-w/2.0,-h/10.0);
  bezierVertex(-w/6.0, -h*11.0/10.0, w/6.0, -h*11.0/10.0, w/2.0, -h/10.0);
  vertex(w/2.0, h/10.0);
  bezierVertex(w/6.0, h*11.0/10.0, -w/6.0, h*11.0/10.0, -w/2.0, h/10.0);
  endShape(CLOSE);
  
  fill(#00FFBD);
  ellipse(0, 0, 2.0*h*3.0/4.0, 2.0*h*3.0/4.0);
 
  fill(0,0,0);
  ellipse(0, 0, h/3.0, h/3.0);
}

おまけ

今回、最初に作った三日月型図形ではなく、楕円を並べて再現してみたものを載せておきます。

楕円の長径の大きさを調整して書籍に掲載されている作品に近づけようと思いましたが、これがなかなかしっくりこなかったので、最終的に三日月型図形で再現することにした次第です。