ここでは、ルートの値を計算するための開平法を利用した作品を紹介していきたいと思います。
Contents
開平法
開平法とは
「ルート」は中学校で以下のように習った記憶があります。
『面積が「\(1\)」の正方形は辺の長さが「\(1\)」、面積が「\(4\)」の正方形は辺の長さが「\(2\)」になります。では、面積が「\(2\)」の正方形の辺の長さはいくつか?
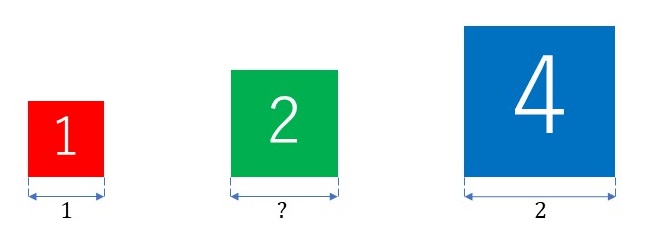
答えは整数ではなく、\(1.414\cdots\)という無理数で、\(\sqrt{2}\)と書き、「ルート2」と読みます。』
こういう感じでしょうか。あとは、\(\sqrt{2}=1.414 \cdots, \ \ \sqrt{3} = 1.732 \cdots, \ \ \sqrt{5} = 2.236 \cdots \)くらいは覚えておいてね、と教わったかな。
このルートの計算方法を中学校では習わなかったですが、もし\(\sqrt{2}\)を計算しようとするならば、以下のようなものでしょうか。
\[ 1.1 \times 1.1 = 1.21, \ \ 1.2 \times 1.2 = 1.44, \ \ 1.3 \times 1.3 = 1.69, \ \ 1.4 \times 1.4 = 1.96, \ \ 1.5 \times 1.5 = 2.25, \ \ \cdots \]で\[ 1.96 \leq 2 <2.25 \]だから、\(\sqrt{2}\)の小数第\(1\)位までは\(1.4\)となる。次に、\[1.41 \times 1.41 =1.9881, \ \ 1.42 \times 1.42 = 2.0164, \ \ \cdots \]で\[ 1.9881 \leq 2 < 2.0164 \]だから、\(\sqrt{2}\)の小数第\(2\)位までは\(1.41\)となる。
という感じで、順々に求めることができます。
しかし実は、足し算、引き算、掛け算、割り算で利用する筆算と同じように、ルートを筆算で計算する方法があります。それが開平法です。
ルートの値を筆算で求める開平法
ここでは、\(\sqrt{2}\)を例にしてルートの値を筆算で求める開平法を説明します。
まず最初に、この筆算の全体像を示します。
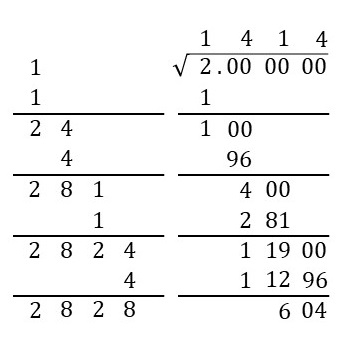
割り算の筆算の形に似てますね。この筆算の右上の数『\(1 \ 4 \ 1 \ 4\)』が\(\sqrt{2}\)の小数第\(3\)位までの値\(1.414\)を表しています。では、この計算の手順を見ていきます。
Step 1
まず、\(\sqrt{2}\)と書きます。このとき、ルートの値を小数第\(n\)位まで求めるならば、ルートの中身(ここでは\(2\))を小数第\(2n\)位まで書いておきます。以下、\(\sqrt{2}\)の値を小数第\(3\)位までを求めることを考えるため、ルートの中身は\(2.000000\)のように小数第\(6\)位まで書いておきます。
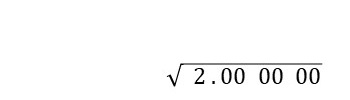
なお、この後のStepで、このルートの左側に数字を書いていくので、ある程度左側は空けておきましょう。
Step 2
次に、\[ 1 \times 1 = 1, \ \ 2 \times 2 = 4 \]で\[1 \leq 2 < 4 \]となるので、\(1\)を\(\sqrt{2}\)の\(2\)の上に書きます。また、\(\sqrt{2}\)の左側にある程度間を空けて、\(1\)を書きます。
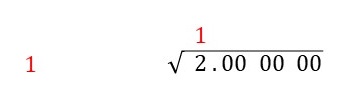
Step 3
Step 2で左側に書いた\(1\)とルートの上側に書いた\(1\)を掛けて、その値を\(2\)の下に書きます(下図の赤字の\(1\))。そして、割り算の筆算のように上の\(2\)から下の\(1\)を引いた値を下に書きます(下図の青字の\(1\))。
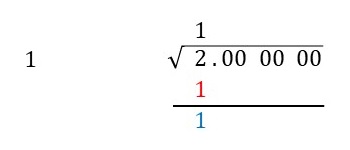
Step 4
Step 2で左側に書いた\(1\)の下に、その値と同じ\(1\)を書きます(下図の赤字の\(1\))。そして、足し算の筆算のように上の\(1\)と下の\(1\)を足した値をその下に書きます(下図の青字の\(2\))。また、右側のルートの中身の小数第\(1\)位と小数第\(2\)位の\(00\)を下におろしてきます(下図の緑色の字\(00\))。
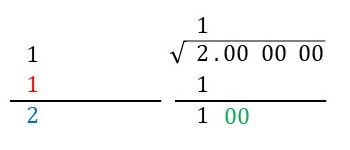
Step 5
Step 4で左側に書いた数\(2\)(下図の青字)を10の位とする数として、それにある適当な1の位の数を加えたものに同じ1の位の数を掛けたものを考えます。この値とStep 4で現れた右側下の数\(100\)(下図の緑色の字)を比較して、\(100\)を越えない一番大きな数になる1の位の数を探します。つまり、\[ 21 \times 1 = 21, \ \ 22 \times 2 = 44, \ \ 23 \times 3 = 69, \ \ 24 \times 4 = 96, \ \ 25 \times 5 = 125, \ \ \cdots \]で、\[ 96 \leq 100 < 125 \]となるので、\(100\)を越えない一番大きな数になる1の位の数は\(4\)となります。この\(4\)を左側の\(2\)の右隣と、ルートの上の\(1\)の右隣にそれぞれ書きます(下図の赤字の\(4\))。
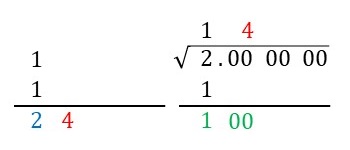
Step 6
Step 5で左側に書いた\(24\)とルートの上側に書いた\(4\)(下図の赤字)を掛けて、その値を右側の下に書いた\(100\)の下に書きます(下図の青字の\(96\))。そして、割り算の筆算のように上の\(100\)から下の\(96\)を引いた値を下に書きます(下図の緑色の字の\(4\))。
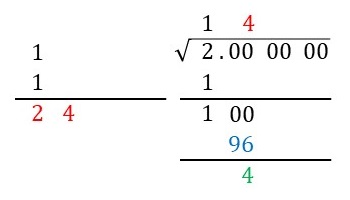
Step 7
Step 5で左側に書いた\(4\)の下に、その値と同じ\(4\)を書きます(下図の赤字の\(4\))。そして、足し算の筆算のように上の\(24\)と下の\(4\)を足した値をその下に書きます(下図の青字の\(28\))。また、右側のルートの中身の小数第\(3\)位と小数第\(4\)位の\(00\)を下におろしてきます(下図の緑色の字\(00\))。
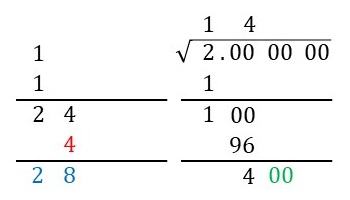
Step 8
Step 7で左側に書いた数\(28\)(下図の青字)を利用してStep 5と同様の処理を行います。つまり、\[ 281 \times 1 = 281, \ \ 282 \times 2 = 564, \ \ \cdots \]で、\[ 281 \leq 400 < 564 \]となるので、\(400\)(下図の緑色の字)を越えない一番大きな数になる1の位の数\(1\)を左側の\(28\)の右隣と、ルートの上の\(14\)の右隣にそれぞれ書きます(下図の赤字の\(1\))。
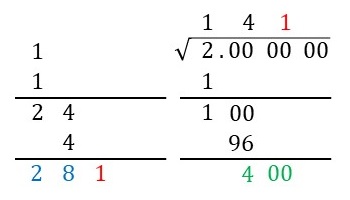
Step 9
あとは、Step 6からStep 8までと同様の処理を求めたいルートの値の桁数まで繰り返します。ちなみに、\(\sqrt{2}\)の値の小数第\(3\)位は、\[2824 \times 4 = 11296, \ \ 2825 \times 5 = 14125 \]で、\[ 11296 \leq 11900 < 14125 \]となるので、\(4\)になることが分かります(下図の赤字の\(4\))。
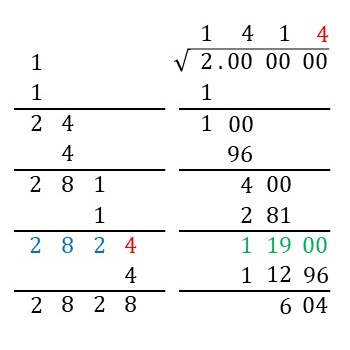
開平法についてもう少し解説
開平法について、もう少し説明しておきます。ただ、上記の計算方法さえ分かっていれば問題ないので、ここは飛ばしても構いません。
任意の正の数を\(A\)として、\(\sqrt{A}\)の値を求めることを考えますが、任意の正の数\(A\)は、\(1 \leq a <100\)となるような\(a\)を用意すると、\[A = a \times 10^{2n} \](\(n\)は整数)と書くことができ、\[ \sqrt{A} = \sqrt{a} \times 10^n \]となるので、ここでは、1以上100未満の任意の正の数\(a\)に対する\(\sqrt{a}\)の値を求めることを考えます。
まず、0以上10未満の整数の値をとる\(a_k\)(\( k=0, 1, 2, \cdots \))を用いて、\(\sqrt{a}\)を\[ \sqrt{a} = \sum_{k=0}^{\infty} a_k 10^{-k} \]と表します。つまり、\(a_k\)は小数第\(k\)位の数を表しています。このとき、\[a = \left( \sum_{k=0}^{\infty} a_k 10^{-k} \right)^2 \]となります。これを書き換えると、\[ a = \sum_{k=0}^{\infty} \left( 2 \sum_{l=0}^{k-1} a_l 10^{-l} + a_k 10^{-k} \right) a_k 10^{-k} \]と書くことができ、最初の数項を見てみると、\[ \begin{equation} a = a_0^2 + (2 a_0 + a_1 10^{-1} ) a_1 10^{-1} + (2 a_0 + 2 a_1 10^{-1} + a_2 10^{-2} ) a_2 10^{-2} + \cdots \tag{*} \end{equation} \]となっていることが分かります。
この形にすると、開平法がどのような計算をしているかが分かってきます。
上記の式\((*)\)の右辺で第1項のみを残すと、\[a > a_0^2 \]の式が成り立ちます。前節で説明したStep 2はこの式が成り立つ最大の\(a_0\)を求めていることが分かります。そして、Step 3は\(a – a_0^2 \)を求めていることがわかります。
次に、 \((*)\)の右辺で第1項を移項し、第2項のみを残すと、\[a – a_0^2 > (2 a_0 + a_1 10^{-1} ) a_1 10^{-1} \]の式が成り立ちます。\(a_0\)は先ほど求めたので、前節で説明したStep 5はこの式が成り立つ最大の\(a_1\)を求めていることが分かります。そして、Step 6は\(a – a_0^2 – (2 a_0 + a_1 10^{-1} ) a_1 10^{-1} \)を求めていることがわかります。
つまり、開平法は式\((*)\)の右辺の各項を段階的に求めていくことで、ルートの値を計算する方法だと考えられます。
開平法のプログラム
開平法をプログラミングする際のポイント
原理的には、開平法は任意の正の数についてルートの値を計算することができます。また、結果は小数になっていますが、計算上は整数の計算と考えて問題ないです。
ただ、プログラミングする際には1つ問題があります。Processingのint型整数は最大\(2147483647\)までの値しかとることができないので、単純にint型整数を利用した開平法を実装しようとすると、ルートの値は数桁しか計算することができません。
そこで、今回はルートの値を格納する変数として、int型の配列を利用することにしました。int型配列を利用することで、100桁でも200桁でも計算することができます(メモリや計算時間が許す限り)。ただし、int型配列で表した整数同士の四則演算や大小比較を行うためのアルゴリズムを別途考える必要があり、そこをうまく実現することがポイントになります。
開平法のプログラムと数学アート
上記のポイントに注意しながら、開平法のプログラムを書きました。なお、今回は1から99までの整数に対するルートを計算するものに限定しています。
// 開平法
int number = 2; // ルートを求めたい整数。現状1から99までの整数
int digit = 100; // 求めたい有効桁数
void setup(){
size(1000,1000,P2D);
int[] root_n = new int[digit]; // root_n[0]は1から9までの整数、その他は0から9までの整数。0番目が最大桁の値。
int[] left_num = new int[digit+1]; // 開平法の左側に出てくる数。各要素は0から9までの整数。0番目が最小桁の値。
int[] right_num = new int[2*digit+1]; // 開平法の右側に出てくる数(差の値に次の桁を加えたもの)。各要素は0から9までの整数。0番目が最小桁の値。
int[] right_num2 = new int[2*digit+1]; // 開平法の右側に出てくる数(left_num × left_num[0])。各要素は0から9までの整数。0番目が最小桁の値。
int[] right_num3 = new int[2*digit+1]; // 開平法の右側に出てくる数(差の値)。各要素は0から9までの整数。0番目が最小桁の値。
int[] forComp = new int[2*digit+1]; // right_num3と比較する値。各要素は0から9までの整数。0番目が最小桁の値。
int left_digit = 1;
int right_digit = 1;
int right_digit2 = 0;
int right_digit3 = 0;
int forComp_digit = 0;
// left_num, right_numを初期化
for(int i=0; i<digit+1; i++){
left_num[i] = 0;
}
for(int i=0; i<2*digit+1; i++){
right_num[i] = 0;
right_num2[i] = 0;
right_num3[i] = 0;
forComp[i] = 0;
}
// rootの整数部分を算出
for(int i=1; i<10; i++){
if( (i+1) * (i+1) > number ){
root_n[0] = i;
break;
}
}
// left_numを更新
left_num[0] = 2 * root_n[0];
if( left_num[0] >= 10 ){
left_num[1] = left_num[0] / 10;
left_num[0] = left_num[0] % 10;
left_digit = 2;
}
// right_numを更新
right_num[0] = number - root_n[0] * root_n[0];
if( right_num[0] >= 10 ){
right_num[1] = right_num[0] / 10;
right_num[0] = right_num[0] % 10;
right_digit = 2;
}
for(int k=1; k<digit; k++){
// left_numの配列を1桁ずつずらす
for(int i=0; i<left_digit; i++){
left_num[left_digit-i] = left_num[left_digit-1-i];
}
left_digit++;
// right_numの配列を2桁ずつずらす
for(int i=0; i<right_digit; i++){
right_num[right_digit+1-i] = right_num[right_digit-1-i];
}
right_num[0] = 0;
right_num[1] = 0;
right_digit += 2;
// root_nのk桁目の値を計算する
left_num[0] = 1; // 0ではなく1を代入 比較は
if( left_digit > right_digit ){
root_n[k] = 0;
continue;
}
boolean flag = false;
if( left_digit == right_digit ){
for(int i=0; i<right_digit; i++){
if( left_num[left_digit-1-i] > right_num[right_digit-1-i] ){
flag = true;
break;
} else if( left_num[left_digit-1-i] < right_num[right_digit-1-i] ){
break;
}
}
if( flag ){
root_n[k] = 0;
left_num[0] = 0;
continue;
}
}
for(int i=1; i<10; i++){
left_num[0] = i;
// left_num × left_num[0] = right_num2
int carry = 0;
for(int j=0; j<left_digit; j++){
right_num2[j] = left_num[j] * left_num[0] + carry;
carry = right_num2[j] / 10;
right_num2[j] = right_num2[j] % 10;
}
right_digit2 = left_digit;
if(carry > 0){
right_digit2++;
right_num2[right_digit2-1] = carry;
}
// right_num - right_num2 = right_num3
int borrow = 0;
for(int j=0; j<right_digit; j++){
if( right_num[j] - borrow < right_num2[j] ){
right_num3[j] = 10 + right_num[j] - borrow - right_num2[j];
borrow = 1;
} else {
right_num3[j] = right_num[j] - borrow - right_num2[j];
borrow = 0;
}
}
right_digit3 = right_digit;
for(int j=0; j<right_digit; j++){
if( right_num3[right_digit-1-j] > 0 ){
break;
} else {
right_digit3--;
}
}
// 比較用の値を算出
forComp_digit = left_digit;
for(int j=0; j<left_digit; j++){
forComp[j] = left_num[j];
}
forComp[0] = 2 * forComp[0] + 1;
carry = 0;
for(int j=0; j<forComp_digit; j++){
int temp = forComp[j] + carry;
forComp[j] = temp % 10;
carry = temp / 10;
}
if( carry > 0 ){
forComp_digit++;
forComp[forComp_digit-1] = carry;
}
flag = false;
if( forComp_digit > right_digit3 ){
flag = true;
}
if( forComp_digit == right_digit3 ){
for(int j=0; j<right_digit3; j++){
if( forComp[forComp_digit-1-j] > right_num3[right_digit3-1-j] ){
flag = true;
break;
} else if( forComp[forComp_digit-1-j] < right_num3[right_digit3-1-j] ){
break;
}
}
}
if( flag ) {
// rootのk桁目の値を確定
root_n[k] = i;
// right_numにright_num3を代入
right_digit = right_digit3;
for(int j=0; j<right_digit3; j++){
right_num[j] = right_num3[j];
}
// left_numを更新
left_num[0] = 2 * left_num[0];
carry = 0;
for(int j=0; j<left_digit; j++){
int temp = left_num[j] + carry;
left_num[j] = temp % 10;
carry = temp / 10;
}
if( carry > 0 ){
left_digit++;
left_num[left_digit-1] = carry;
}
break;
}
}
}
print("root_n ");
for(int i=0; i<digit; i++){
print(root_n[i]);
}
// 開平法の結果を使って、作図
background(255,255,255);
int diameter = width / digit;
int shift = diameter / 2;
strokeWeight(diameter);
for(int i=0; i<digit; i++){
for(int j=0; j<digit; j++){
if(j<i){
stroke(25 * root_n[i], 25 * root_n[i], 25 * root_n[i]);
} else {
stroke(25 * root_n[j], 25 * root_n[j], 25 * root_n[j]);
}
point(i * diameter + shift, j * diameter + shift);
}
}
save("extractionOfSquareRoot.jpg");
} また、その結果を利用して数学アートを描いてみました。
今回は特に\(\sqrt{2}\)の値を小数第\(99\)位まで求めました。\[ \sqrt{2} =1.414213562373095048801688724209698078569665904835246916153479755535048279162589106829979776517455242 \]そして、各小数の位の値を用いてグレースケールでの色の濃淡を表した円を縦横に順に並べることで図形を作成しました。
