魔女・女王
ここでは、書籍「パソコンで描く紋様とデザイン コンピュータグラフィックスの新しい試み」のp.15,16に掲載されている図形の中から「魔女」や「女王」のように見える図形があったので、それらを Processingで再現してみました。
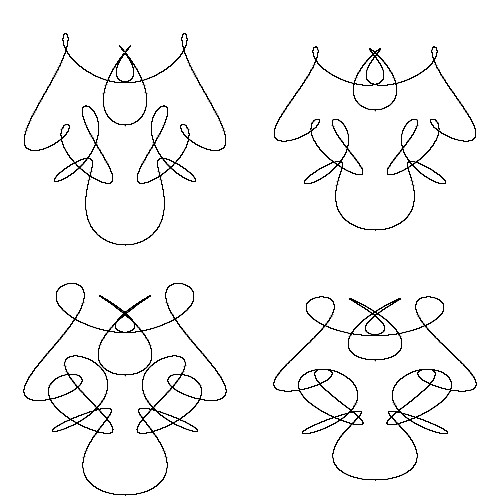
リサージュ曲線(パラメータ)
これらの図形は\(N=3\)のリサージュ曲線を利用していて、それらのパラメータは以下のようになります。
\[ x(t) = A_1 \sin ( \omega_{x,1} t + \theta_{x,1})+A_2 \sin ( \omega_{x,2} t + \theta_{x,2})+A_3 \sin ( \omega_{x,3} t + \theta_{x,3}) , \\ y(t) = B_1 \sin ( \omega_{y,1} t + \theta_{y,1})+ B_2 \sin ( \omega_{y,2} t + \theta_{y,2}) + B_3 \sin ( \omega_{y,3} t + \theta_{y,3}) \]
左上の図形のパラメータ
| \(n=1\) | \(n=2\) | \(n=3\) | |
| \(x\)方向の振幅\(A_n\) | 60 | 30 | 15 |
| \(x\)方向の周波数\(\omega_{x,n}\) | 1 | 4 | 14 |
| \(x\)方向の位相\(\omega_{x,n}\) | 0 | 0 | 0 |
| \(y\)方向の振幅\(B_n\) | 60 | 30 | 30 |
| \(y\)方向の周波数\(\omega_{y,n}\) | 1 | 4 | 10 |
| \(y\)方向の位相\(\omega_{y,n}\) | 90 | 90 | 90 |
右上の図形のパラメータ
| \(n=1\) | \(n=2\) | \(n=3\) | |
| \(x\)方向の振幅\(A_n\) | 60 | 30 | 15 |
| \(x\)方向の周波数\(\omega_{x,n}\) | 1 | 4 | 14 |
| \(x\)方向の位相\(\omega_{x,n}\) | 0 | 0 | 0 |
| \(y\)方向の振幅\(B_n\) | 60 | 20 | 25 |
| \(y\)方向の周波数\(\omega_{y,n}\) | 1 | 4 | 10 |
| \(y\)方向の位相\(\omega_{y,n}\) | 90 | 90 | 90 |
左下の図形のパラメータ
| \(n=1\) | \(n=2\) | \(n=3\) | |
| \(x\)方向の振幅\(A_n\) | 60 | 20 | 25 |
| \(x\)方向の周波数\(\omega_{x,n}\) | 1 | 4 | 14 |
| \(x\)方向の位相\(\omega_{x,n}\) | 0 | 0 | 0 |
| \(y\)方向の振幅\(B_n\) | 60 | 30 | 30 |
| \(y\)方向の周波数\(\omega_{y,n}\) | 1 | 4 | 10 |
| \(y\)方向の位相\(\omega_{y,n}\) | 90 | 90 | 90 |
右下の図形のパラメータ
| \(n=1\) | \(n=2\) | \(n=3\) | |
| \(x\)方向の振幅\(A_n\) | 60 | 20 | 25 |
| \(x\)方向の周波数\(\omega_{x,n}\) | 1 | 4 | 14 |
| \(x\)方向の位相\(\omega_{x,n}\) | 0 | 0 | 0 |
| \(y\)方向の振幅\(B_n\) | 60 | 20 | 25 |
| \(y\)方向の周波数\(\omega_{y,n}\) | 1 | 4 | 10 |
| \(y\)方向の位相\(\omega_{y,n}\) | 90 | 90 | 90 |
プログラムコード
以下にこれらの図形を描くためのプログラムコードを紹介します。
void setup(){
size(500,500);
background(255,255,255);
noFill();
int N = 3; // 項数
// 魔女1
translate(width/4.0, height/4.0);
float[] r1_x = {60.0, 30.0, 15.0};
float[] omega1_x = {1.0, 4.0, 14.0};
float[] theta1_x = {0.0, 0.0, 0.0};
float[] r1_y = {60.0, 30.0, 30.0};
float[] omega1_y = {1.0, 4.0, 10.0};
float[] theta1_y = {90.0, 90.0, 90.0};
float cycle1 = 1.0;
drawLissajous(N, r1_x, omega1_x, theta1_x, r1_y, omega1_y, theta1_y, cycle1);
// 魔女2
translate(width/2.0, 0.0);
float[] r2_x = {60.0, 30.0, 15.0};
float[] omega2_x = {1.0, 4.0, 14.0};
float[] theta2_x = {0.0, 0.0, 0.0};
float[] r2_y = {60.0, 20.0, 25.0};
float[] omega2_y = {1.0, 4.0, 10.0};
float[] theta2_y = {90.0, 90.0, 90.0};
float cycle2 = 1.0;
drawLissajous(N, r2_x, omega2_x, theta2_x, r2_y, omega2_y, theta2_y, cycle2);
// 虫の女王1
translate(-width/2.0, height/2.0);
float[] r3_x = {60.0, 20.0, 25.0};
float[] omega3_x = {1.0, 4.0, 14.0};
float[] theta3_x = {0.0, 0.0, 0.0};
float[] r3_y = {60.0, 30.0, 30.0};
float[] omega3_y = {1.0, 4.0, 10.0};
float[] theta3_y = {90.0, 90.0, 90.0};
float cycle3 = 1.0;
drawLissajous(N, r3_x, omega3_x, theta3_x, r3_y, omega3_y, theta3_y, cycle3);
// 虫の女王2
translate(width/2.0, 0.0);
float[] r4_x = {60.0, 20.0, 25.0};
float[] omega4_x = {1.0, 4.0, 14.0};
float[] theta4_x = {0.0, 0.0, 0.0};
float[] r4_y = {60.0, 20.0, 25.0};
float[] omega4_y = {1.0, 4.0, 10.0};
float[] theta4_y = {90.0, 90.0, 90.0};
float cycle4 = 1.0;
drawLissajous(N, r4_x, omega4_x, theta4_x, r4_y, omega4_y, theta4_y, cycle4);
}
// リサージュ曲線を描く関数
void drawLissajous(
int N, // 項数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y, // y方向の位相に関する配列
float cycle // 回転数
){
float x, y;
int num = 10000;
beginShape();
for(int i=0; i<num*cycle; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * sin( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
vertex(x,y);
}
endShape();
}