ここでは、\(N=2\)のリサージュ図形において2つ目の波形を回転した場合の効果について考えてみます。
2つ目の波形の効果(復習)
\( N=2 \)でのリサージュ曲線は以下の式で表すことができます。
\[ x(t) = A_1 \cos ( \omega_{x,1} t + \theta_{x,1})+A_2 \cos ( \omega_{x,2} t + \theta_{x,2}) , \\ y(t) = B_1 \sin ( \omega_{y,1} t + \theta_{y,1})+ B_2 \sin ( \omega_{y,2} t + \theta_{y,2}) \]
\(N=2\)の場合、\(x\)方向、\(y\)方向共に2つの三角関数の重ね合わせとなっています。そして、\(A_1 \geq A_2, \ \ B_1 \geq B_2 \)とすると、重ね合わせは大きい振幅\(A_1, \ \ B_1 \)の波形に対して2つ目の小さい振幅\(A_2, \ \ B_2 \)の波形が付け加わるような形になります。このとき、2つ目の波形の効果について考えます。
具体的には、\(x(t)\)と\(y(t)\)の振幅と位相を固定して、2つ目の波形の周波数を変化させていった場合の図形を考えてみます。\[ A_1 = B_1 = R = 60, \ \ A_2=B_2=r=30, \ \ \omega_{x,1}=\omega_{y,1}=\Omega =1, \ \ \theta_{x,1} = \theta_{y,1} = 0, \ \ \theta_{x,2} =\theta_{y,2} = 0 \]そして、\( \omega_{x,2}= \omega_{y,2}=\omega = 2,3,4,5 \)と変化させて描いたリサージュ図形が下図上段、また、2つ目の波形が1つ目の波形と反対方向に変化するときのリサージュ曲線がどのように表示されるか見るために、 \( \omega_{x,2}= \omega_{y,2}=\omega=-2,-3,-4,-5 \)と変化させた場合の図形が下図下段となります。
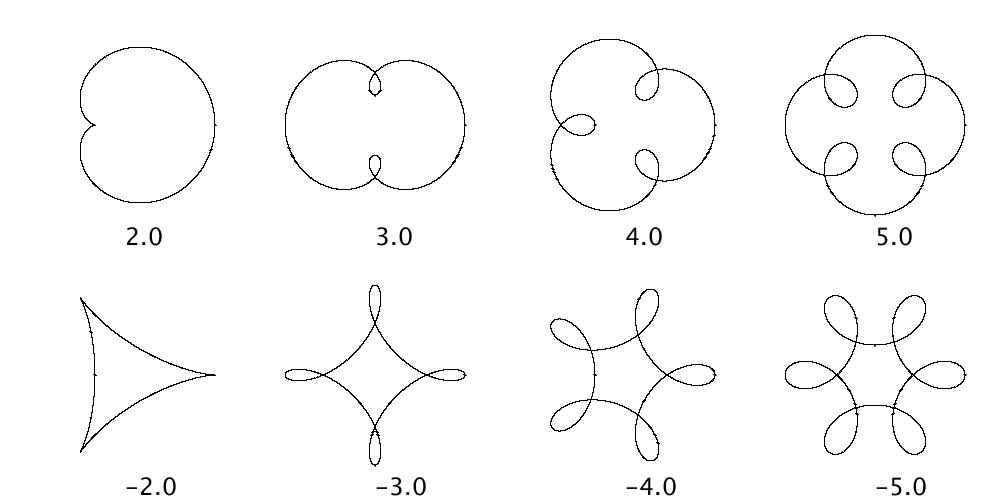
1つ目の波形と2つ目の波形との周波数の符号が同じである場合は、2つ目の波形の効果は内向きになっていることが分かります。また、内向きの出っ張りの数は\( \omega_{x,2} / \omega_{x,1}-1\)個となっていることがわかります。
一方、 1つ目の波形と2つ目の波形との周波数の符号が異なる場合は、2つ目の波形の効果は外向きになっています。 また、外向きの出っ張りの数は\( \omega_{x,2} / \omega_{x,1}+1\)個となっていることがわかります。
2つ目の波形の回転の効果
今度は記事「リサージュ図形の回転に関する考察」で解説したように、2つ目の波形を1つ目の波形に垂直になるように回転することを考えます。今回の場合、この回転は\[ r \cos \omega t \to r \cos \{ (\omega + \Omega )t -45 \} \\ r \sin \omega t \to r \sin \{ (\omega + \Omega )t -45 \} \]となります。これを1つ目の波形の式\( ( R \cos \Omega t, R \sin \Omega t ) \)に加えることで求めたい図形が得られます。
では、この回転の効果をみるために、回転しない場合と回転した場合について\( \omega_{x,2}= \omega_{y,2}=\omega = 2,3,4,5 \)と変化させたリサージュ図形を描いてみます。
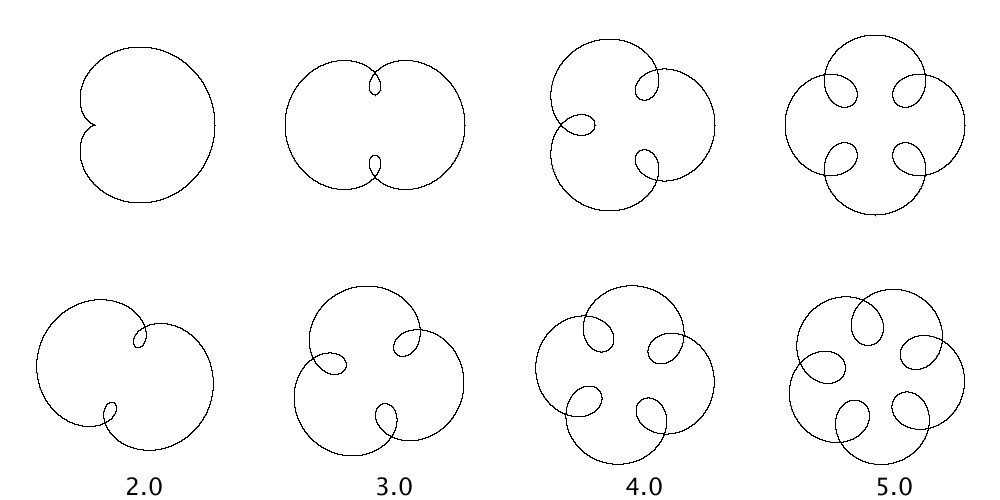
上段が2つ目の波形を回転しない場合で、下段が2つ目の波形を回転した場合です。今回の1つの面白い特徴として、回転しない場合の内向きの出っ張りの数は\( \omega_{x,2} / \omega_{x,1}-1\)個になっていたことに対して、回転した場合の内向きの出っ張りの数は\( \omega_{x,2} / \omega_{x,1}\)個になっており、周波数の比と同じ数になっていることが分かります。
また、同様にして、1つ目の波形と2つ目の波形との周波数の符号が異なる場合として、\( \omega_{x,2}= \omega_{y,2}=\omega=-2,-3,-4,-5 \)と変化させたリサージュ図形を描いてみると以下のようになります。
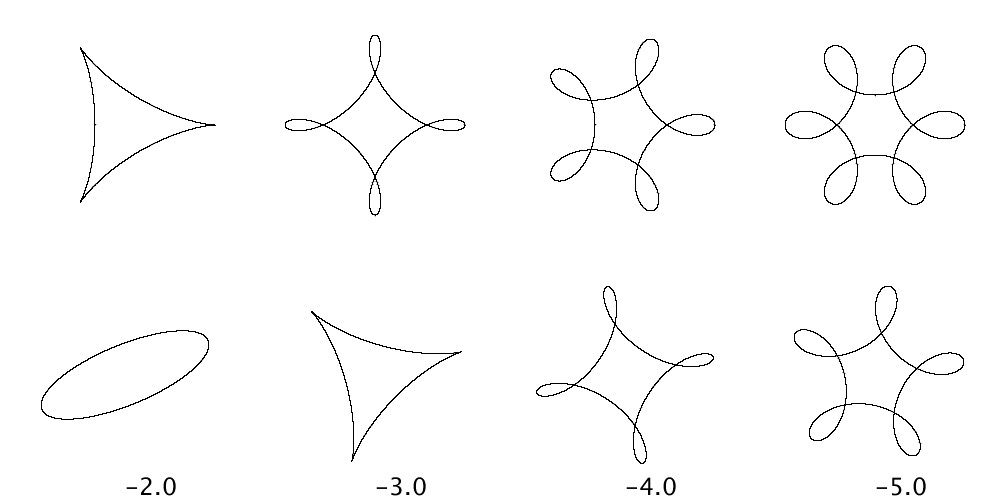
周波数が異符号の場合も、回転しない場合の外向きの出っ張りの数は\( \omega_{x,2} / \omega_{x,1}+1\)個になっていたことに対して、回転した場合の外向きの出っ張りの数は\( \omega_{x,2} / \omega_{x,1}\)個になっており、周波数の比と同じ数になっていることが分かります。
このように、周波数比と出っ張りの数が同じになるということはリサージュ図形を利用して作品を作っていく際に考えやすくなると思います。
ソースコード
今回の図形のソースコードを示しておきます。なお、25行目と26行目の符号を変えることで、周波数が同符号の場合と異符号の場合とに切り替えることができます。
void setup(){
size(1000,500);
background(255,255,255);
noFill();
// N=2のリサージュ曲線
// 周波数を変化させる
float[] r_x = {60.0, 30.0};
float[] omega_x = {1.0, 1.0};
float[] theta_x = {0.0, 0.0};
float[] r_y = {60.0, 30.0};
float[] omega_y = {1.0, 1.0};
float[] theta_y = {0.0, 0.0};
float cycle = 1.0;
// 2つ目の波形を回転させるときのパラメータ
float omega = omega_x[0];
float theta = -45.0;
for(int i=0; i<4; i++){
// 2つ目の波形の回転前
resetMatrix();
translate(width/4.0*(i+0.5), height/4.0);
omega_x[1] = (i+2.0); // -(i+2.0);
omega_y[1] = (i+2.0); // -(i+2.0);
noFill();
drawLissajous(2, r_x, omega_x, theta_x, r_y, omega_y, theta_y, cycle);
// 2つ目の波形の回転後
resetMatrix();
translate(width/4.0*(i+0.5), height*3.0/4.0);
omega_x[1] = omega_x[1] + omega;
omega_y[1] = omega_y[1] + omega;
theta_x[1] = theta;
theta_y[1] = theta;
noFill();
drawLissajous(2, r_x, omega_x, theta_x, r_y, omega_y, theta_y, cycle);
String freq = String.valueOf(omega_x[1] - omega_y[0]);
fill(0,0,0);
textSize(24);
text(freq, 0.0, 120.0);
}
}
// リサージュ曲線を描く関数
void drawLissajous(
int N, // 項数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y, // y方向の位相に関する配列
float cycle // 回転数
){
float x, y;
int num = 10000;
beginShape();
for(int i=0; i<num*cycle; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * cos( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
vertex(x,y);
}
endShape();
}