リサージュ図形(\(N=2\))
ここでは、\( N=2 \)でのリサージュ図形について考えます。
\[ x(t) = A_1 \sin ( \omega_{x,1} t + \theta_{x,1})+A_2 \sin ( \omega_{x,2} t + \theta_{x,2}) , \\ y(t) = B_1 \sin ( \omega_{y,1} t + \theta_{y,1})+ B_2 \sin ( \omega_{y,2} t + \theta_{y,2}) \]
\(N=2\)の場合、\(x\)方向、\(y\)方向共に2つの三角関数の重ね合わせとなっています。このサイトでは、\(A_1 \geq A_2, \ \ B_1 \geq B_2 \)としているので、この重ね合わせは大きい振幅\(A_1, \ \ B_1 \)の軌道に対して小さい振幅\(A_2, \ \ B_2 \)の軌道が付け加わるような形になります。
2つ目の波形の効果
では2つ目の波形の効果について考えてみます。\(x(t)\)と\(y(t)\)の振幅と位相を固定して、2つ目の波形の周波数を変化させていった場合の図形を考えてみます。具体的には、
\[ A_1 = B_1 = 60, \ \ A_2=B_2=30, \ \ \omega_{x,1}=\omega_{y,1}=1, \ \ \theta_{x,1} = 0, \ \ \theta_{y,1} = 90 \]
として、\( \omega_{x,2}= \omega_{y,2}=2,3,4,5 \)と変化させて描いています(下図上段)。また、2つ目の波形が1つ目の波形と反対方向に変化するときのリサージュ曲線がどのように表示されるか見るために、 \( \omega_{x,2}= \omega_{y,2}=-2,-3,-4,-5 \)と変化させた場合の図形も描いています(下図下段)。
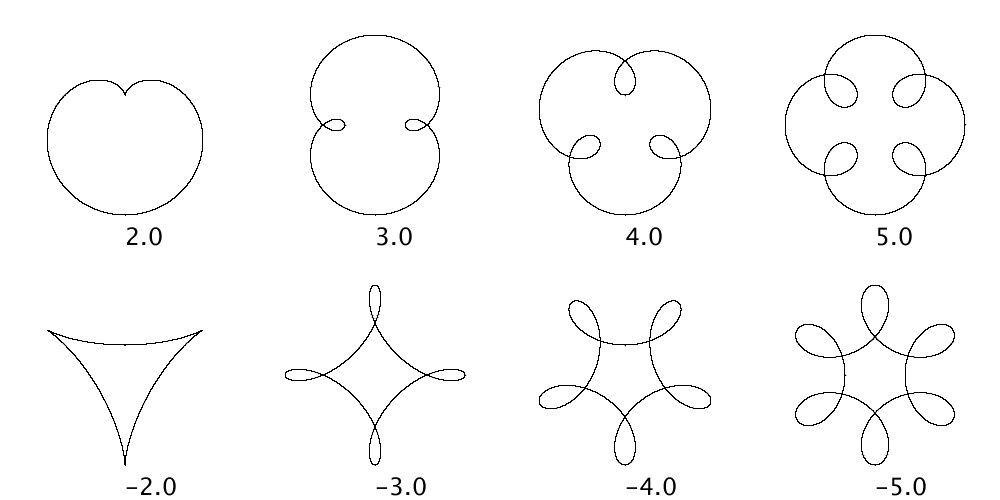
1つ目の波形と2つ目の波形との周波数の符号が同じである場合は、2つ目の波形の効果は内向きになっていることが分かります。また、内向きの出っ張りの数は\( \omega_{x,2}-1\)個となっていることがわかります。ただし、\(\omega_{x,1}=\omega_{y,1}=1\)の場合にのみ成り立ちます。 \(\omega_{x,1}=\omega_{y,1} \neq 1\)の場合はまた変わってきます。
一方、 1つ目の波形と2つ目の波形との周波数の符号が異なる場合は、2つ目の波形の効果は外向きになっています。 また、外向きの出っ張りの数は\( \omega_{x,2}+1\)個となっていることがわかります。
これらの図形を描くためのプログラムコード(Processing)は以下のようになります。
void setup(){
size(1000,500);
background(255,255,255);
noFill();
int N = 2; // 項数
// 周波数を変化させる
float[] r1_x = {60.0, 30.0};
float[] omega1_x = {1.0, 1.0};
float[] theta1_x = {0.0, 0.0};
float[] r1_y = {60.0, 30.0};
float[] omega1_y = {1.0, 1.0};
float[] theta1_y = {90.0, 90.0};
float cycle = 1.0;
for(int j=0; j<2; j++){
for(int i=0; i<4; i++){
resetMatrix();
translate(width/4.0*(i+0.5), height/2.0*(j+0.5));
omega1_x[1] = (i+2.0)*pow(-1,j);
omega1_y[1] = (i+2.0)*pow(-1,j);
noFill();
drawLissajous(N, r1_x, omega1_x, theta1_x, r1_y, omega1_y, theta1_y, cycle);
String freq = String.valueOf(omega1_x[1]);
fill(0,0,0);
textSize(24);
text(freq, 0.0, 120.0);
}
}
}
// リサージュ曲線を描く関数
void drawLissajous(
int N, // 項数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y, // y方向の位相に関する配列
float cycle // 回転数
){
float x, y;
int num = 10000;
beginShape();
for(int i=0; i<num*cycle; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * sin( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
vertex(x,y);
}
endShape();
}1つ目の波形と2つ目の波形との周波数比
前節では、 \(\omega_{x,1}=\omega_{y,1}=1\)の場合を考えましたが、今度は\(\omega_{x,1}=\omega_{y,1}=1.5\)にしてみます。 結果は以下の通りです。
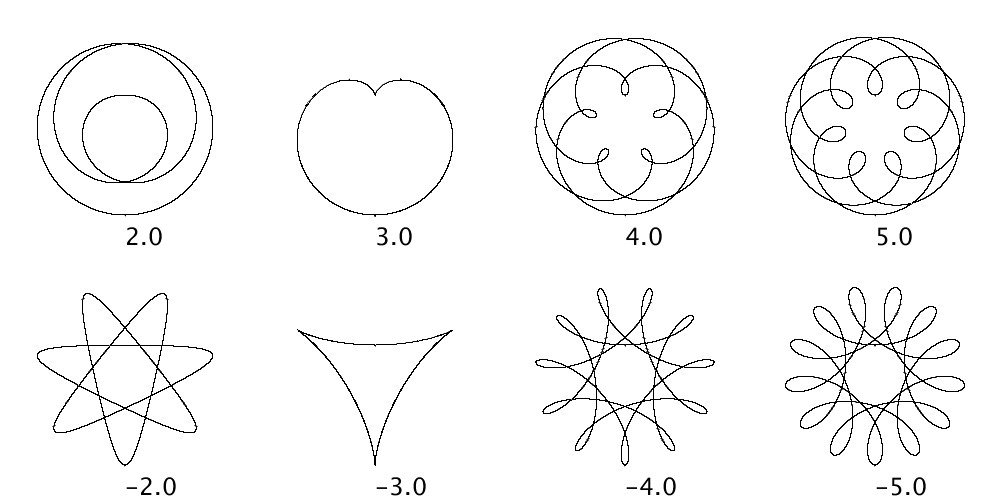
\(\omega_{x,1}\)と\(\omega_{x,2}\)との周波数比を変えるだけで、いろいろなバリエーションの図形が描くことができます。ちなみに、2列目の図形は前節の1列目の図形と同じになっているのは、ここで説明している周波数比が同じだからです。また、これらの図形の軌道を指で追っていくと、出っ張りが描かれる順番が結構複雑であることがわかり、おもしろいです。
以下、プログラムコードです。
void setup(){
size(1000,500);
background(255,255,255);
noFill();
int N = 2; // 項数
// 周波数を変化させる
float[] r1_x = {60.0, 30.0};
float[] omega1_x = {1.5, 1.0};
float[] theta1_x = {0.0, 0.0};
float[] r1_y = {60.0, 30.0};
float[] omega1_y = {1.5, 1.0};
float[] theta1_y = {90.0, 90.0};
float cycle = 4.0;
for(int j=0; j<2; j++){
for(int i=0; i<4; i++){
resetMatrix();
translate(width/4.0*(i+0.5), height/2.0*(j+0.5));
omega1_x[1] = (i+2.0)*pow(-1,j);
omega1_y[1] = (i+2.0)*pow(-1,j);
noFill();
drawLissajous(N, r1_x, omega1_x, theta1_x, r1_y, omega1_y, theta1_y, cycle);
String freq = String.valueOf(omega1_x[1]);
fill(0,0,0);
textSize(24);
text(freq, 0.0, 120.0);
}
}
}
// リサージュ曲線を描く関数
void drawLissajous(
int N, // 項数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y, // y方向の位相に関する配列
float cycle // 回転数
){
float x, y;
int num = 10000;
beginShape();
for(int i=0; i<num*cycle; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * sin( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
vertex(x,y);
}
endShape();
}