リサージュ図形（N=1）

  1. ホーム
  2. リサージュ図形
  3. リサージュ図形（N=1）

リサージュ図形（\(N=1\)）

ここでは、\( N=1 \)でのリサージュ図形について考えます。

\[ x(t) = A_1 \sin ( \omega_{x,1} t + \theta_{x,1}), \ \ y(t) = B_1 \sin ( \omega_{y,1} t + \theta_{y,1}) \]

なお、一般的にリサージュ図形やリサージュ曲線と言えば、この\(N=1\)の場合に相当するようですが、ここではより一般的な\(N \geq 2\)の場合も含めて、リサージュ図形やリサージュ曲線と呼んでいます。

位相を変化させる

\(x(t)\)と\(y(t)\)の振幅と周波数を同じにして、位相を変化させていった場合の図形を考えてみます。具体的には、

\[ A_1 = B_1 = 60, \ \ \omega_{x,1} = \omega_{y,1} = 1, \ \ \theta_{x,1} = 0 \]

として、\( \theta_{y,1} \)を0°から360°まで15°ずつ変化させて描いています。

位相の変化

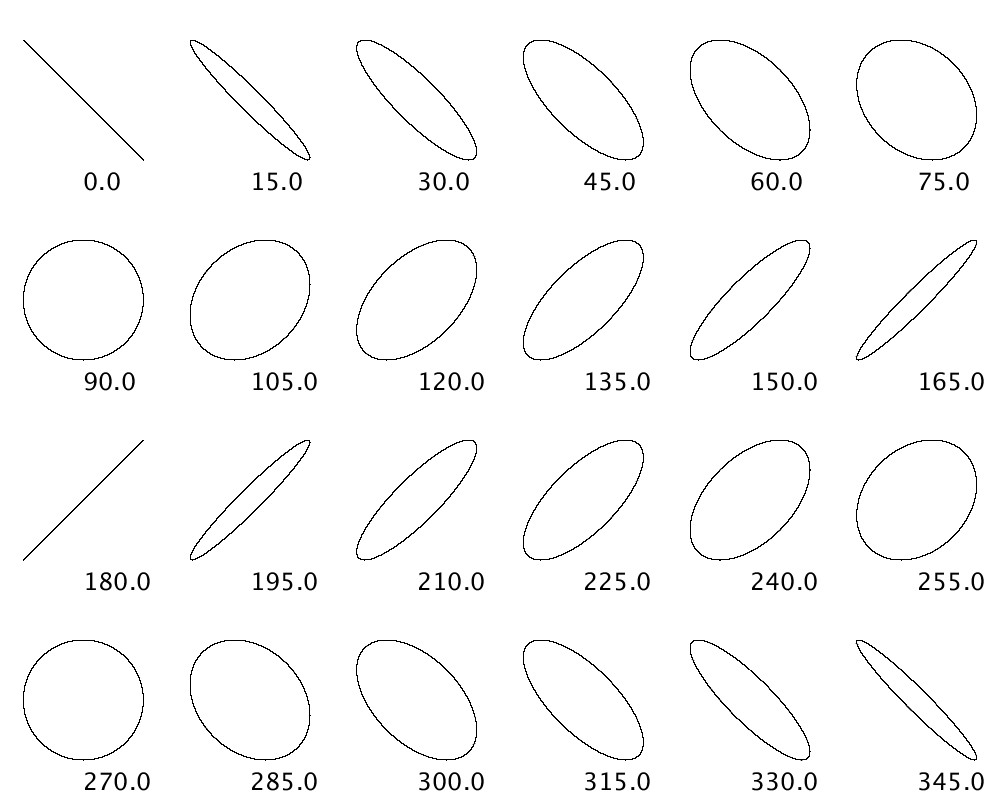
最初位相がそろっている段階では直線となり、位相が少しずつずれていくと楕円形、位相差が90°になったとき円になることが分かります。位相差が90°を越えるとまた楕円形をたどり、180°で0°と直交する直線になります。直線から楕円形、そして円、また楕円形を経て、直線に戻るというのを繰り返していきます。

これらの図形を描くためのプログラムコード（Processing）を載せておきます。

void setup(){
  size(1000,800);
  background(255,255,255);

  int N = 1; // 項数
  // y方向の位相を変化させる
  float[] r1_x = {60.0};
  float[] omega1_x = {1.0};
  float[] theta1_x = {0.0};
  float[] r1_y = {60.0};
  float[] omega1_y = {1.0};
  float[] theta1_y = {0.0};
  for(int j=0; j<4; j++){
    for(int i=0; i<6; i++){
      resetMatrix();
      translate(width/6.0*(i+0.5), height/4.0*(j+0.5));
      theta1_y[0] = 15 * (6*j+i);
      noFill();
      drawLissajous(N, r1_x, omega1_x, theta1_x, r1_y, omega1_y, theta1_y);
      String angle = String.valueOf(theta1_y[0]);
      fill(0,0,0);
      textSize(24);
      text(angle, 0.0, 90.0);
    }
  }
}

// リサージュ曲線を描く関数
void drawLissajous(
  int N, // 項数
  float[] r_x, // x方向の振幅に関する配列
  float[] omega_x, // x方向の周波数に関する配列
  float[] theta_x, // x方向の位相に関する配列
  float[] r_y, // y方向の振幅に関する配列
  float[] omega_y, // y方向の周波数に関する配列
  float[] theta_y // y方向の位相に関する配列
){
  float x, y;
  int num = 10000;
 
  beginShape();
  for(int i=0; i<num; i++){
    x = 0.0;
    y = 0.0;
    for(int j=0; j<N; j++){
      x += r_x[j] * sin( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
      y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
    }
    vertex(x,y);
  }
  endShape();
}

周波数を変化させる

次は\(x(t)\)と\(y(t)\)の振幅と位相を固定して、周波数を変化させていった場合の図形を考えてみます。具体的には、

\[ A_1 = B_1 = 60, \ \ \theta_{x,1} = 0, \ \ \theta_{y,1} = 90 \]

として、\( \omega_{x,1} \)と\( \omega_{y,1} \)との比を変化させて描いています。

周波数比が有理数の場合

周波数比の変化

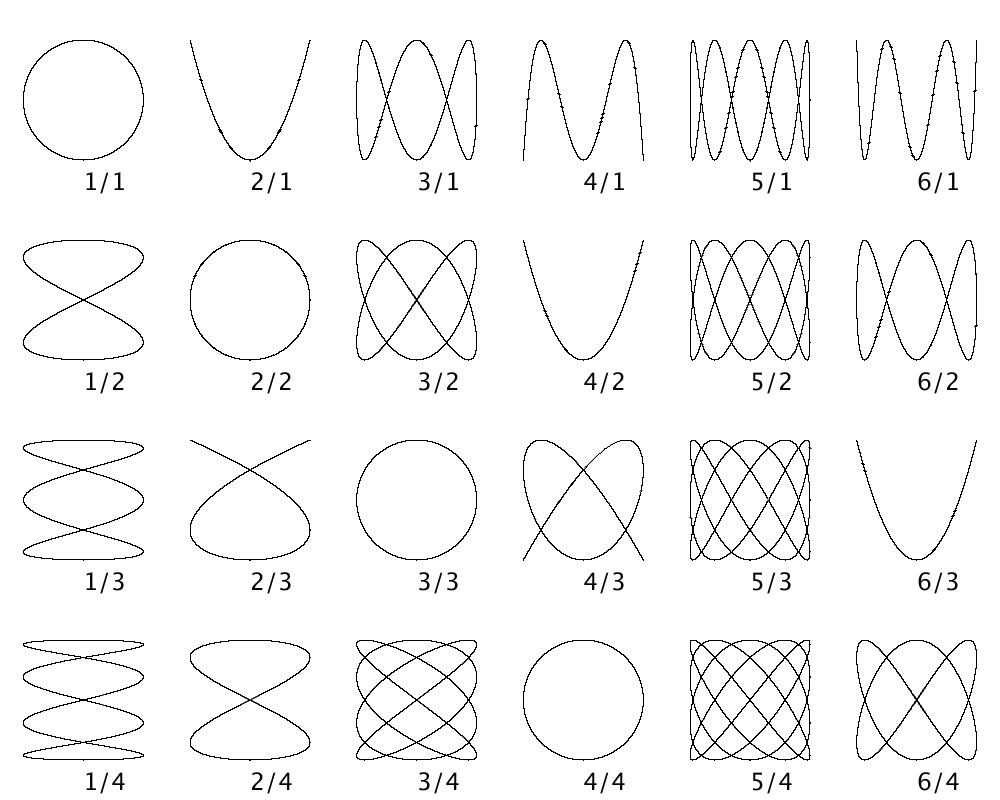
各図形の下にある数値は分母が\(x\)方向の周波数 \( \omega_{x,1} \)の値、分子が\(y\)方向の周波数 \( \omega_{y,1} \)の値をそれぞれ表しています。

これらの図形を眺めているだけでもいろいろなことを考えてしまいます。例えば、周波数比が\(2:3\)と\(3:2\)とでなぜこんなに形が違うのか、なんからの関係性はあるのか、など。リサージュ図形の奥深さを感じさせられます。

プログラムコードは以下です。

void setup(){
  size(1000,800);
  background(255,255,255);
  noFill();

  int N = 1; // 項数
  // 周波数を変化させる
  float[] r1_x = {60.0};
  float[] omega1_x = {1.0};
  float[] theta1_x = {0.0};
  float[] r1_y = {60.0};
  float[] omega1_y = {1.0};
  float[] theta1_y = {90.0};
  float cycle = 4.0;
  for(int j=0; j<4; j++){
    for(int i=0; i<6; i++){
      resetMatrix();
      translate(width/6.0*(i+0.5), height/4.0*(j+0.5));
      omega1_y[0] = (i+1.0)/(j+1.0);
      noFill();
      drawLissajous(N, r1_x, omega1_x, theta1_x, r1_y, omega1_y, theta1_y, cycle);
      String freq = String.valueOf(i+1) + "/" + String.valueOf(j+1);
      fill(0,0,0);
      textSize(24);
      text(freq, 0.0, 90.0);
    }
  }
}

// リサージュ曲線を描く関数
void drawLissajous(
  int N, // 項数
  float[] r_x, // x方向の振幅に関する配列
  float[] omega_x, // x方向の周波数に関する配列
  float[] theta_x, // x方向の位相に関する配列
  float[] r_y, // y方向の振幅に関する配列
  float[] omega_y, // y方向の周波数に関する配列
  float[] theta_y, // y方向の位相に関する配列
  float cycle // 回転数
){
  float x, y;
  int num = 10000;
 
  beginShape();
  for(int i=0; i<num*cycle; i++){
    x = 0.0;
    y = 0.0;
    for(int j=0; j<N; j++){
      x += r_x[j] * sin( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
      y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
    }
    vertex(x,y);
  }
  endShape();
}

周波数比が無理数の場合

周波数比が無理数の場合

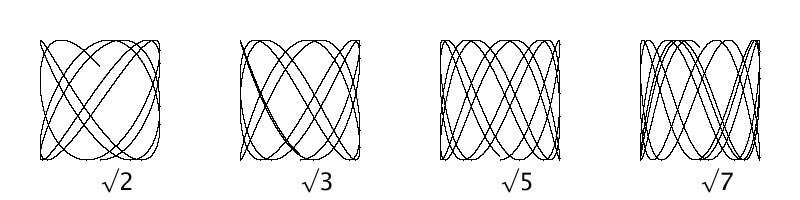
各図形の下にある数値は\(x\)方向の周波数が\(1\)のときの\(y\)方向の周波数をそれぞれ表しています。

周波数比が無理数の場合、リサージュ曲線の軌道は閉じることはありません。\(t\)をいくら大きくしても常に異なる軌道を描き続けます。

プログラムコードは以下です。

void setup(){
  size(800,200);
  background(255,255,255);
  noFill();

  int N = 1; // 項数
  // 周波数を変化させる
  float[] r1_x = {60.0};
  float[] omega1_x = {1.0};
  float[] theta1_x = {0.0};
  float[] r1_y = {60.0};
  float[] omega1_y = {1.0};
  float[] theta1_y = {90.0};
  float cycle = 4.0;
  int[] omega = {2, 3, 5, 7};
  for(int i=0; i<4; i++){
    resetMatrix();
    translate(width/4.0*(i+0.5), height/2.0);
    omega1_y[0] = sqrt(omega[i]);
    noFill();
    drawLissajous(N, r1_x, omega1_x, theta1_x, r1_y, omega1_y, theta1_y, cycle);
    String freq = "√" + String.valueOf(omega[i]);
    fill(0,0,0);
    textSize(24);
    text(freq, 0.0, 90.0);
  }
}

// リサージュ曲線を描く関数
void drawLissajous(
  int N, // 項数
  float[] r_x, // x方向の振幅に関する配列
  float[] omega_x, // x方向の周波数に関する配列
  float[] theta_x, // x方向の位相に関する配列
  float[] r_y, // y方向の振幅に関する配列
  float[] omega_y, // y方向の周波数に関する配列
  float[] theta_y, // y方向の位相に関する配列
  float cycle // 回転数
){
  float x, y;
  int num = 10000;
 
  beginShape();
  for(int i=0; i<num*cycle; i++){
    x = 0.0;
    y = 0.0;
    for(int j=0; j<N; j++){
      x += r_x[j] * sin( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
      y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
    }
    vertex(x,y);
  }
  endShape();
}

コメントを残す