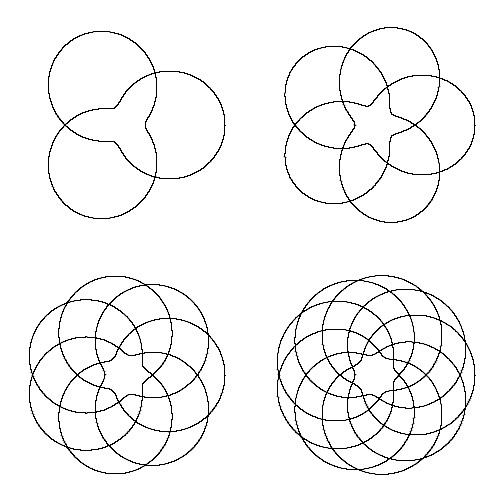
書籍「マス・アート~真理、美、そして方程式~」で紹介されていたリサージュ図形を基本とした作品の数々。リサージュ図形の可能性に興味を惹かれました。
Contents
リサージュ曲線
このサイトで作成していきたい作品は、以下のパラメータ表示された、リサージュ曲線を用いて描いていきたいと思います。
\[ x(t) = \sum_{n=1}^{N} A_n \sin ( \omega_{x,n} t + \theta_{x,n}), \ \ y(t) = \sum_{n=1}^{N} B_n \sin ( \omega_{y,n} t + \theta_{y,n}) \]
ここで、\( A_n, \ \ B_n \)は振幅、\( \omega_{x,n}, \ \ \omega_{y,n} \)は周波数、そして\( \theta_{x,n}, \ \ \theta_{y,n} \)は位相をそれぞれ表しています。また、\[ A_1 \geq A_2 \geq \cdots \geq A_N, \ \ B_1 \geq B_2 \geq \cdots \geq B_N \]を満たします。
\(N\)は項数を表しています。この値が大きくなれば、より複雑でより豊かな美しい図形を描いていくことができます。
これらの値を設定してパラメータ\(t\)を動かしていくことで\(xy\)平面上にさまざまな図形を描いていくことができます。
リサージュ曲線を描くための関数のプログラムコードをここで紹介しておきます。以降でさまざまなリサージュ図形を描いていくときに利用しています。
// リサージュ曲線を描く関数
void drawLissajous(
int N, // 項数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y, // y方向の位相に関する配列
float cycle // 回転数
){
float x, y;
int num = 10000;
beginShape();
for(int i=0; i<num*cycle; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * sin( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
vertex(x,y);
}
endShape();
}リサージュ図形(\(N=1\))
\( N=1 \)でのリサージュ図形について考えます。この場合のリサージュ曲線は以下のようになります。
\[ x(t) = A_1 \sin ( \omega_{x,1} t + \theta_{x,1}), \ \ y(t) = B_1 \sin ( \omega_{y,1} t + \theta_{y,1}) \]
なお、一般的にリサージュ図形やリサージュ曲線と言えば、この\(N=1\)の場合に相当するようですが、ここではより一般的な\(N \geq 2\)の場合も含めて、リサージュ図形やリサージュ曲線と呼んでいます。
ここでは、まず\(x\)方向と\(y\)方向とで、位相をずらした場合と周波数をずらした場合について考察しています。
リサージュ図形(\(N=2\))
\( N=2 \)でのリサージュ図形について考えます。 この場合のリサージュ曲線は以下のようになります。
\[ x(t) = A_1 \sin ( \omega_{x,1} t + \theta_{x,1})+A_2 \sin ( \omega_{x,2} t + \theta_{x,2}) , \\ y(t) = B_1 \sin ( \omega_{y,1} t + \theta_{y,1})+ B_2 \sin ( \omega_{y,2} t + \theta_{y,2}) \]
ここでは、大きい振幅\(A_1, \ \ B_1 \)の軌道に対して小さい振幅\(A_2, \ \ B_2 \)の軌道を加えることでどのような図形が描けるかを見ていきたいと思います。
リサージュ図形(\(N=3\))
ここでは、\( N=3 \)でのリサージュ図形を用いた作品を紹介します。
\[ x(t) = A_1 \sin ( \omega_{x,1} t + \theta_{x,1})+A_2 \sin ( \omega_{x,2} t + \theta_{x,2})+A_3 \sin ( \omega_{x,3} t + \theta_{x,3}) , \\ y(t) = B_1 \sin ( \omega_{y,1} t + \theta_{y,1})+ B_2 \sin ( \omega_{y,2} t + \theta_{y,2}) + B_3 \sin ( \omega_{y,3} t + \theta_{y,3}) \]
ギャラリー
まず、書籍「パソコンで描く紋様とデザイン コンピュータグラフィックスの新しい試み」のp.15,16に掲載されていたものから面白いと思ったものを選び、Processingで再現したものになります。なお、キャプションをクリックすると、そのプログラムコードを見ることができます。
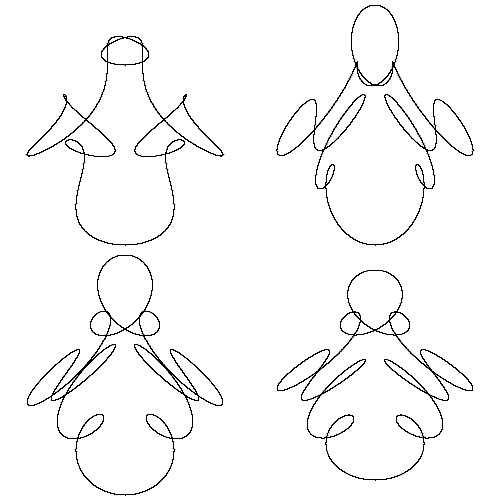
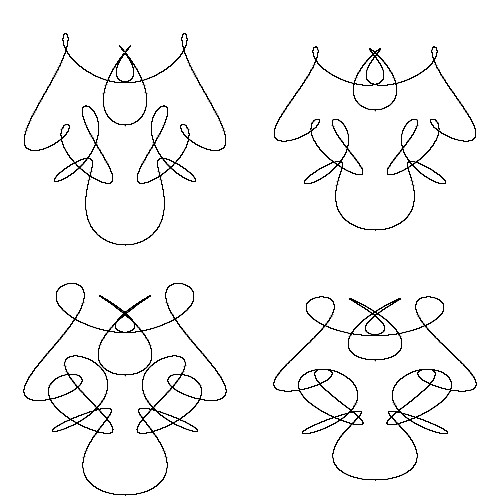
次に、書籍「非線形ダイナミクスとカオス」のp.302,303で解説されているトーラス結び目をリサージュ図形として描いてみました。 キャプションをクリックすると、トーラス結び目とリサージュ図形との関係についての解説とそのプログラムコードを見ることができます。
鉄の魔神
ここでは、書籍「マス・アート~真理、美、そして方程式~」のp.133で紹介されていた鉄の魔神という装置で描かれたリサージュ図形の再現を試みています。

トーラス型コイル
ここでは、リサージュ図形の形の変形の例として、トーラス型コイルと呼ぶ図形を描くことを考えてみます。

リサージュ図形の回転に関する考察
ここでは、\(N=2\)以上のリサージュ図形において、振幅の大きさが大きな軌道(主軌道と呼ぶことにします)に、振幅の大きさが小さくて周波数が主軌道よりも大きい軌道(副軌道と呼ぶことにします)を加えるとき、副軌道のリサージュ曲線を主軌道に対して垂直に交わるように回転することを考えます。
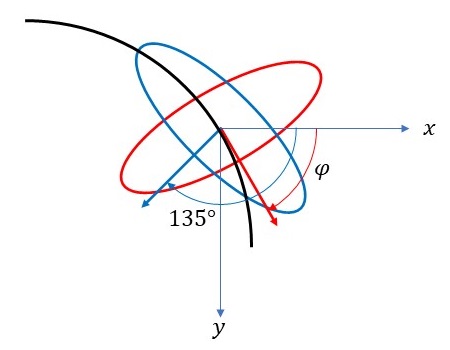
リサージュ図形(\(N=2\)) 2つ目の波形の回転
ここでは、\(N=2\)のリサージュ図形において2つ目の波形を回転した場合の効果について考えてみます。
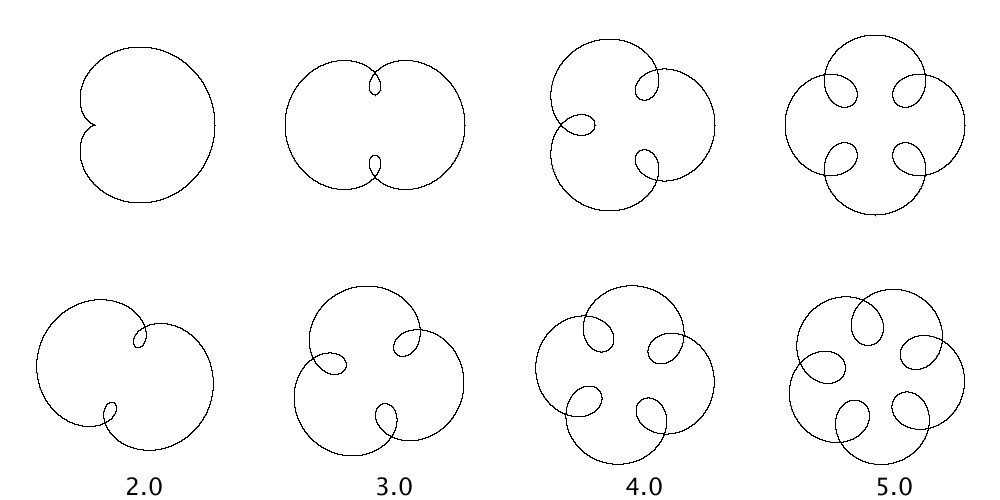
拡張されたリサージュ図形
記事「リサージュ図形の回転に関する考察」において、sin, cos関数の引数がパラメータtの線形関数ではなく、非線形になるようなものを考え、これを拡張されたリサージュ図形として考えてはどうかと示唆しました。ここでは、この拡張されたリサージュ図形を描いてみます。

参考文献
今回のリサージュ図形を用いた作品を考える際に参考にした文献を以下に示しておきます。