ゼッケンドルフ表現

  1. ホーム
  2. 黄金比
  3. ゼッケンドルフ表現

書籍「アートで魅せる数学の世界」のp.41-43で、フィボナッチ数に関する定理「ゼッケンドルフの定理」を用いた図形が紹介されています。今回はこれを再現してみました。

ゼッケンドルフの定理

ゼッケンドルフの定理とは、

『どんな自然数に対してもただ１つのゼッケンドルフ表現が定まる。』

というものです。つまり、\[ \begin{align} 31 &= 21 + 8 + 2 \\ 43 &= 34 +8 +1 \\ 53 & = 34 + 13 + 5 +1 \\ 77 &= 55 + 21 + 1 \end{align} \]のように、自然数をフィボナッチ数だけの和で表すことができ、その表現が一通りしかないというものになります。これをゼッケンドルフ表現と呼びます。

なお、記事「フィボナッチ数列による螺旋」で紹介していますが、フィボナッチ数列とは、以下のような数列です。\[ 0, \ \ 1, \ \ 1, \ \ 2, \ \ 3, \ \ 5, \ \ 8, \ \ 13, \ \ 21, \ \ 34, \ \ 55, \ \ 89, \ \ 144, \ \ \cdots \]特徴として、ある数はその前の2つの数の和になっています。

ゼッケンドルフ表現による図形１

では、書籍「アートで魅せる数学の世界」のp.42で紹介されているゼッケンドルフ表現による図形を再現してみたいと思います。結果は、以下のような図形になりました。

ゼッケンドルフ表現による図形１

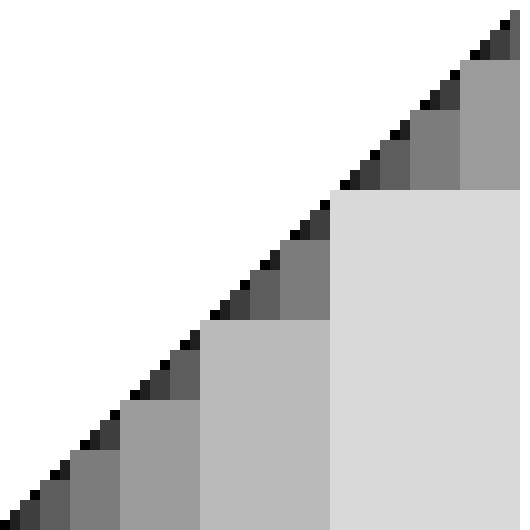
書籍では、それぞれの長方形の色がサイズごとにカラフルに色分けされていますが、ここではフィボナッチ数の値に合わせてグレースケールで表現しています。

この図形は、次の手順で描くことができます。

  1. 「1から53までの自然数」を考えます。なお、53という数値はフィボナッチ数列の21までの和を表しています。
  2. それぞれの自然数をゼッケンドルフ表現を利用してフィボナッチ数の和に分解していきます。例えば、31の場合は、\(31 = 21 + 8 + 2\)のように分解できます。
  3. 分解したフィボナッチ数のそれぞれの値を縦の長さとし、横の長さを\(1\)とした長方形を準備し、大きい方から順に縦に積み上げていきます。例えば、31の場合は縦横の長さがそれぞれ\(21 \times 1, \ \ 8 \times 1, \ \ 2 \times 1\)をもつ長方形を用意し、それらを順に縦方向に積み上げていきます。
  4. 3の手順を「1から53までの自然数」に対して行い、作成した長方形を積み上げたものを左から順に並べていくことで完成します。

ソースコード

このゼッケンドルフ表現による図形を描くためのプログラムのソースコードを示しておきます。

void setup(){
  size(530,530);
  background(255,255,255);
  translate(0, height);
  scale(1,-1);
  noStroke();
  
  // フィボナッチ数列
  int n = 8;
  int[] fibo = new int[n];
  fibo[0] = 1;
  fibo[1] = 2;
  for(int i=2; i<n; i++){
    fibo[i] = fibo[i-1] + fibo[i-2];
  }
  
  // フィボナッチ数列のn-1個までの和
  int fibo_sum = 0;
  for(int i=0; i<n-1; i++){
    fibo_sum += fibo[i];
  }

  int[] index = new int[n];
  int index_count;
  int remainder;
  int h;
  int color_unit = 255 / n;
  int cell_size = 10;
  for(int i=1; i<fibo_sum; i++){
    remainder = i;
    index_count = 0;
    // 整数iのゼッケンドルフ表現を算出
    for(int j=n-1; j>=0; j--){
      if( remainder >= fibo[j] ){
        remainder -= fibo[j];
        index[index_count] = j;
        index_count++;
      }
    }
    
    // ゼッケンドルフ表現を用いた図形の描画
    h=0;
    for(int j=0; j<index_count; j++){
      fill(color_unit * index[j]);
      rect((i-1)*cell_size, h*cell_size, cell_size, fibo[index[j]]*cell_size);
      h += fibo[index[j]];
    }
  }
}

ゼッケンドルフ表現による図形2

次に、書籍「アートで魅せる数学の世界」のp.43で紹介されている2つ目のゼッケンドルフ表現による図形を再現してみたいと思います。結果は、以下のような図形になりました。

ゼッケンドルフ表現による図形2

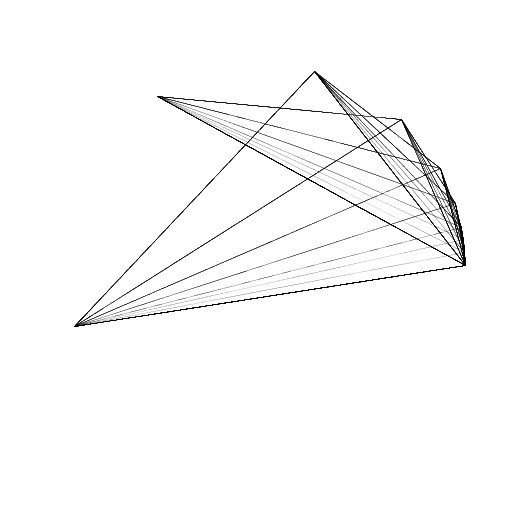
この図形は、次の手順で描くことができます。

  1. 「1から87までの自然数」を考えます。なお、87という数値はフィボナッチ数列の34までの和を表しています。
  2. それぞれの自然数をゼッケンドルフ表現を利用してフィボナッチ数の和に分解していきます。例えば、31の場合は、\(31 = 21 + 8 + 2\)のように分解できます。
  3. 分解したフィボナッチ数のそれぞれの値に合わせて、円周上に点を取っていき、それらの点をつなげていきます。このとき、円の中心から右向きに向いた直線と円が交わる点を基準にして円周上に点をとります。また、点をつなげていく際はこの基準点をスタートとゴールにします。例えば、円周を100等分したとき、31の場合は等分した円周の角度の2倍、8倍、21倍の位置に点を打ち、基準点から始めて順に線分で結んでいきます。
  4. 3の手順を「1から87までの自然数」に対して行い、それぞれの図形を描画していくことで完成します。

ソースコード

この2つ目のゼッケンドルフ表現による図形を描くためのプログラムのソースコードを示しておきます。

void setup(){
  size(530,530);
  background(255,255,255);
  translate(width/2.0, height/2.0);
  scale(1,-1);
  strokeWeight(0.1);
  
  // フィボナッチ数列
  int n = 9;
  int[] fibo = new int[n];
  fibo[0] = 1;
  fibo[1] = 2;
  for(int i=2; i<n; i++){
    fibo[i] = fibo[i-1] + fibo[i-2];
  }
  
  // フィボナッチ数列のn-1個までの和
  int fibo_sum = 0;
  for(int i=0; i<n-1; i++){
    fibo_sum += fibo[i];
  }

  int[] index = new int[n];
  int index_count;
  int remainder;
  int divide_num = 100; // 円周の分割数
  float degree_unit = 2.0 * PI / divide_num; // 分割した円周の角度
  float r = 200.0; // 円の半径
  float theta1, theta2;
  for(int i=1; i<fibo_sum; i++){
    remainder = i;
    index_count = 0;
    // 整数iのゼッケンドルフ表現を算出
    for(int j=n-1; j>=0; j--){
      if( remainder >= fibo[j] ){
        remainder -= fibo[j];
        index[index_count] = j;
        index_count++;
      }
    }
    
    // ゼッケンドルフ表現を用いた図形の描画
    theta1 = 0.0;
    theta2 = 0.0;
    for(int j=index_count-1; j>=0; j--){
      theta2 = degree_unit * fibo[index[j]];
      line(r * cos( theta1 ), r * sin( theta1 ), r * cos( theta2 ), r * sin( theta2 ));
      theta1 = theta2;
    }
    theta2 = 0.0;
    line(r * cos( theta1 ), r * sin( theta1 ), r * cos( theta2 ), r * sin( theta2 ));
  }
}