貴金属比による螺旋

書籍「アートで魅せる数学の世界」のp.19-21で紹介されている貴金属比を用いた疑似的な螺旋の再現を試みています。

Contents

1 貴金属比とは
2 貴金属比による螺旋
3 ソースコード
4 おまけ：白銀比（\(n=2\)）を持つ長方形による正八角形

貴金属比とは

下図のような、短辺の長さが\(1\)、長辺の長さが\(x\)である長方形（黒色）を考えます。

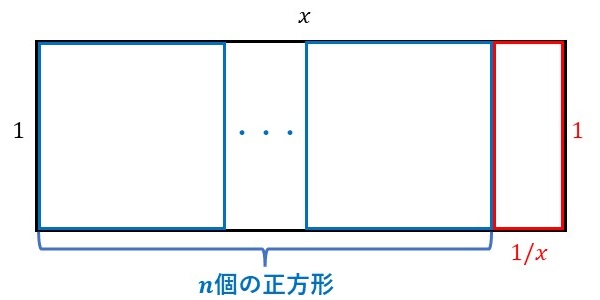
黄金比の場合、長方形から、辺の長さが\(1\)の正方形部分を取り除きました。貴金属比では、この長方形から、辺の長さが\(1\)の正方形を\(n\)個取り除きます。このとき、残った部分の長方形（赤色）が元の長方形（黒色）と相似になるとき、長方形の縦と横の長さの比を貴金属比（Metallic ratio）と呼びます。

なお、貴金属比の値\(x\)は、\[ x-n = \frac{1}{x} \ \ \to \ \ x = \frac{n+\sqrt{n^2+4}}{2} \] で与えられます。

なお、\(n=2\)のとき、\(x=1+\sqrt{2}\)となり、この場合特別に白銀比と呼びます。白銀比は\(1:\sqrt{2}\)の場合も白銀比と言いますので、混同しないように注意が必要です。また、\(n=3\)のときも特別な呼び方があり、青銅比（Bronze ratio）と呼びます。

貴金属比による螺旋として、今回は白銀比（\(1:1+\sqrt{2}\)）と青銅比による螺旋を再現してみました。

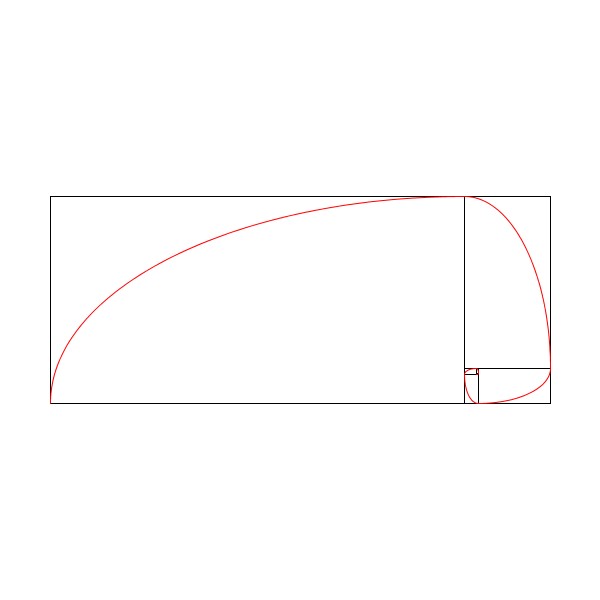
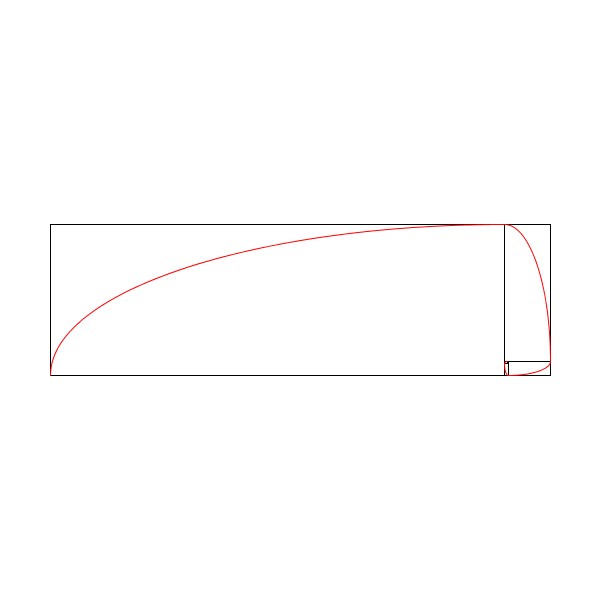
これらの図形は、貴金属比をもつ長方形を、\(n\)個の正方形と長方形に順に分割したものに合わせて、長方形の辺の短辺と長辺の長さをそれぞれ短半径と長半径とした楕円の円弧を描くことで作成することができます。なお、円弧をつないだものですので、実際の螺旋とはことなります。そのため、疑似的な螺旋としています。

ソースコード

この貴金属比を用いた疑似的な螺旋を描くプログラムのソースコードを示しておきます。

  size(600,600);
  background(255,255,255);
  noFill();
  
  int n = 3;
  float phi = (n+sqrt(n*n+4.0))/2.0; // 貴金属比
  float len = 500.0/ phi; // 一番大きい長方形の短辺の長さ
  translate(width/2.0 + len*phi/2.0, height/2.0 + len/2.0);
  
  // 扇形の中心位置
  PVector center = new PVector(0.0,0.0);
  PVector opposite = new PVector(0.0,0.0);
  PVector direction = new PVector(1.0, 0.0);
  int count = 0;
  float theta;
  rectMode(CORNERS);
  while( len > 1.0 ){
    theta = radians(90.0) * ((count+2)%4);
    center.add( direction.copy().mult(len/phi).rotate(theta) );
    opposite = center.copy().add( direction.copy().mult(sqrt(n*n+1.0)*len).rotate(theta + atan(1.0/n)) );
    stroke(0,0,0);
    rect(center.x, center.y, opposite.x, opposite.y);
    stroke(255,0,0);
    if(count%2 == 0){
      arc(center.x, center.y, 2.0*len*n, 2.0*len, theta, theta + radians(90.0));
    } else {
      arc(center.x, center.y, 2.0*len, 2.0*len*n, theta, theta + radians(90.0));
    }
    len *= 1.0/phi;
    count++;
  }
}

おまけ：白銀比（\(n=2\)）を持つ長方形による正八角形

白銀比（\(n=2\)）を持つ長方形をその中心を軸にして45°ずつ回転して４つ重ねると、正八角形が描けます。

一応そのソースコードも示しておきます。

void setup(){
  size(600,600);
  background(255,255,255);
  translate(width/2.0, height/2.0);

  noStroke();
  fill(0,0,255,64);
  rectMode(CENTER);

  float phi = 1.0 + sqrt(2.0);
  float L1 = 200.0;
  float L2 = L1 * phi;
  for(int i=0; i<4; i++){
    rotate(radians(45.0));
    rect(0.0, 0.0, L1, L2);
  }
}