黄金三角形 - 数学アートの部屋

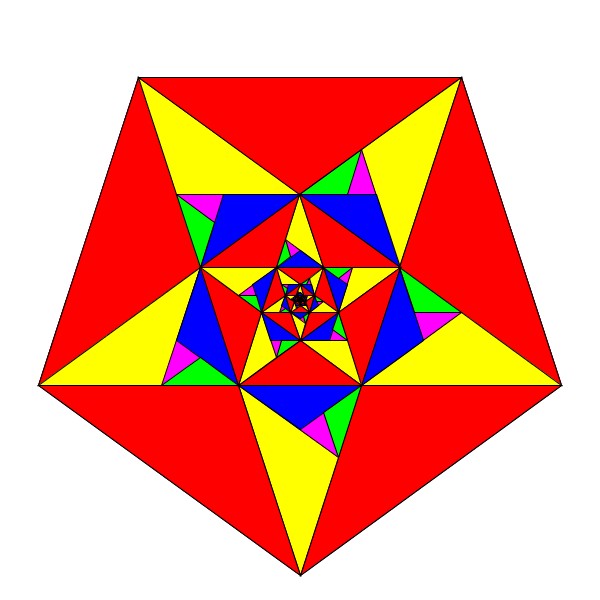
ここでは、書籍「アートで魅せる数学の世界」のp.22-26で紹介されている黄金三角形に関連する図形について再現を試みています。

Contents

1 黄金三角形とは
2 黄金三角形の分割
3 疑似的な螺旋のソースコード
4 黄金三角形を用いた図形

黄金三角形とは

黄金三角形とは、各頂点での角度が36°、72°、72°となる二等辺三角形のことを指します。

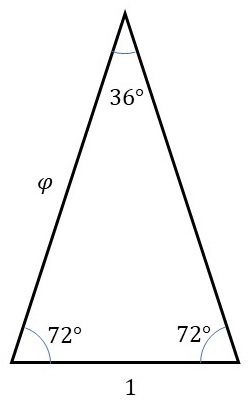
この二等辺三角形の等辺と底辺の長さの比が黄金比\(\varphi\)と一致しており、それにちなんで黄金三角形と呼ばれているようです。

黄金三角形の分割

黄金三角形は、下の図のように108°、36°、36°となる二等辺三角形（下図の青色の三角形、「黄金グノーモン」と呼ばれます）と小さい黄金三角形（下図の赤色の三角形）に分割することができます。

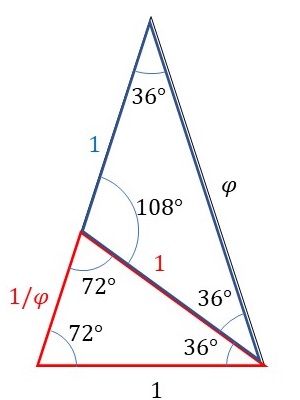
この黄金三角形の分割を新たにできた小さい黄金三角形に対して繰り返していき、各黄金グノーモンの等辺の長さを半径とする扇型を描いていくことで、次のような疑似的な螺旋を描くことができます。

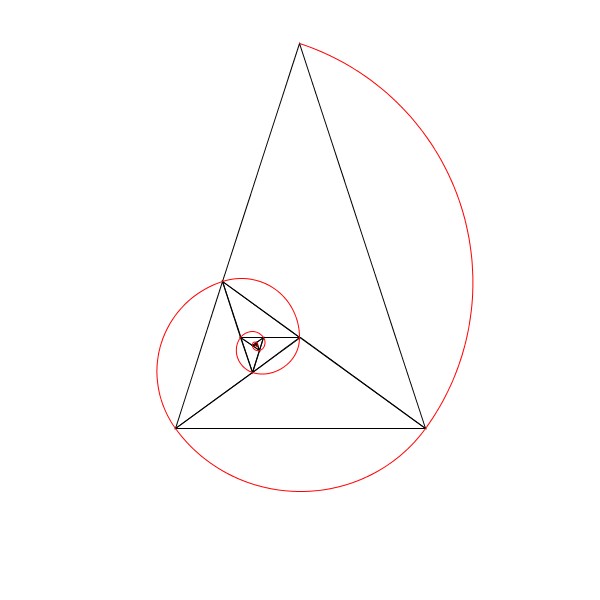
疑似的な螺旋のソースコード

この黄金三角形を用いた疑似的な螺旋を描くプログラムのソースコードを示しておきます。

void setup(){
  size(600,600);
  background(255,255,255);
  noFill();
  
  float phi = (1.0+sqrt(5.0))/2.0; // 黄金比
  float len = 250.0; // 一番大きい黄金三角形の底辺の長さ
  translate(width/2.0-len/2.0, height/2.0+ len*sqrt(phi*phi-0.25)/3.0);
  
  // 扇形（グノーモン）に関するパラメータ
  float theta1 = -radians(180.0);
  float theta2 = -radians(72.0);
  PVector center = new PVector(0.0,0.0);
  PVector vertex1 = PVector.fromAngle(theta1).mult(len * phi);
  PVector vertex2 = PVector.fromAngle(theta2).mult(len * phi);
//    triangle(center.x, center.y, vertex1.x, vertex1.y, vertex2.x, vertex2.y);

  while( len > 1.0 ){
    theta1 += radians(108.0);
    theta2 += radians(108.0);
    center.add( PVector.fromAngle(theta1).mult(len/phi) );
    vertex1 = PVector.fromAngle(theta1).mult(len).add( center.copy() );
    vertex2 = PVector.fromAngle(theta2).mult(len).add( center.copy() );
    stroke(0,0,0);
    triangle(center.x, center.y, vertex1.x, vertex1.y, vertex2.x, vertex2.y);
    stroke(255,0,0);
    arc(center.x, center.y, 2.0*len, 2.0*len, theta1, theta2);
    len *= phi-1.0;
  }

}

黄金三角形を用いた図形

その他、書籍「アートで魅せる数学の世界」のp.26で紹介されている黄金三角形に関連する図形について再現してみました。