Ｌシステム - 数学アートの部屋

ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形アルケミスト双書」のp.8,9に掲載されていたＬシステムの例であるレヴィＣ曲線やドラゴン曲線について、自分でも作ってみました。

Contents

1 Ｌシステムとは
2 レヴィC曲線
- 2.1 プログラムコード
3 ドラゴン曲線
- 3.1 プログラムコード

Ｌシステムとは

書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形アルケミスト双書」のp.8でコッホ曲線を例に解説されているものが分かりやすいので、それに沿って説明します。

コッホ曲線を描くときの最初の段階を次のように表現します。

１ステップ前進（A）、左に60°回転（＋）、１ステップ前進（A）、右に60°回転（－）、もう一度右に60°回転（－）、１ステップ前進（A）、左に60°回転（＋）、１ステップ前進（A）

これを「Ａ＋Ａ－－Ａ＋Ａ：60°」で表します。この中の１ステップ前進（A）を「Ａ＋Ａ－－Ａ＋Ａ：60°」で置き換えることにより、コッホ曲線を描くときの次の段階を表現することができます。これを無限に繰り返すことで、コッホ曲線が得られます。

このように表現した式をＬシステムと呼びます。

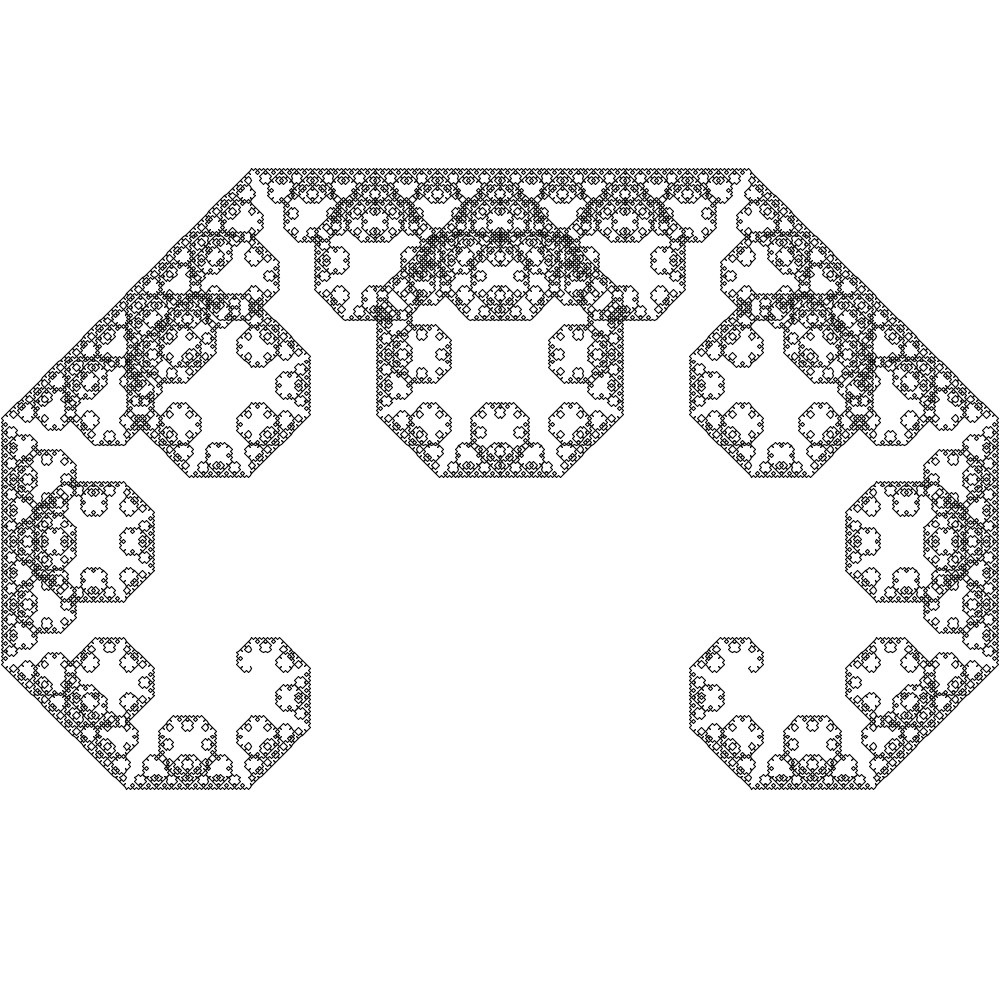
レヴィC曲線

レヴィC曲線はＬシステムで表すと「＋A－－A＋：45°」となります。Aの部分をさらに「＋A－－A＋：45°」で置き換えていきます。

プログラムコード

レヴィC曲線を描くプログラムコードを載せておきます。

float h_min = 5.0; // 枝の長さの最小値

void setup(){
  size(1000,1000);
  background(255,255,255);
  
  // レヴィC曲線
  PVector start = new PVector(width/4.0, height*2.0/3.0);
  PVector end = new PVector(3.0*width/4.0, height*2.0/3.0);
  drawLevyC(start, end);
}

// レビィC曲線を描くための関数
void drawLevyC(PVector start, PVector end){
  // レビィC曲線を描くための新たな頂点を算出
  PVector sub_vec = end.copy().sub(start.copy());
  PVector levy_point = PVector.add(start.copy(), sub_vec.copy().mult(1.0/sqrt(2.0)).rotate(radians(-45)));

  // レヴィC曲線を再帰的に描画する
  if(sub_vec.mag() > h_min){
    drawLevyC(start, levy_point);
    drawLevyC(levy_point, end);
  } else {
    line(start.x, start.y, levy_point.x, levy_point.y);
    line(levy_point.x, levy_point.y, end.x, end.y);
  }
}

ドラゴン曲線

ドラゴン曲線はＬシステムで表すと「＋A－－B＋：45°」となります。ただし、Aの部分は「＋A－－B＋：45°」で置き換えますが、Bの部分は「－A＋＋B－：45°」で置き換えていきます。AもBも上記の解説で言えば「１ステップ前進」ではありますが、置き換え方が変わるので区別しています。

プログラムコード

ドラゴン曲線を描くプログラムコードを載せておきます。

float h_min = 10.0; // 枝の長さの最小値

void setup(){
  size(1000,1000);
  background(255,255,255);
  
  // ドラゴン曲線
  PVector start = new PVector(width/4.0, height/2.0);
  PVector end = new PVector(3.0*width/4.0, height/2.0);
  drawDragon(start, end);
}

// ドラゴン曲線を描くための関数
void drawDragon(PVector start, PVector end){
  // startとendで結ばれる線分を3分割する点
  PVector sub_vec = end.copy().sub(start.copy());
  PVector dragon_point = PVector.add(start.copy(), sub_vec.copy().mult(1.0/sqrt(2.0)).rotate(radians(-45)));

  // ドラゴン曲線を描画する
    drawDragon_recur(start, dragon_point, 45);
    drawDragon_recur(dragon_point, end, -45);
} 

// ドラゴン曲線を描く際、再帰的に呼び出す関数
void drawDragon_recur(PVector start, PVector end, float theta){
  // ドラゴン曲線を描くための新たな頂点を算出
  PVector sub_vec = end.copy().sub(start.copy());
  PVector dragon_point = PVector.add(start.copy(), sub_vec.copy().mult(1.0/sqrt(2.0)).rotate(radians(-theta)));

  // ドラゴン曲線を再帰的に描画する
  if(sub_vec.mag() > h_min){
    drawDragon_recur(start, dragon_point, 45);
    drawDragon_recur(dragon_point, end, -45);
  } else {
    line(start.x, start.y, dragon_point.x, dragon_point.y);
    line(dragon_point.x, dragon_point.y, end.x, end.y);
  }
}