ジュリア集合２

ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形アルケミスト双書」のp.34,35に掲載されていたジュリア集合による図形を作ってみました。なお、同じジュリア集合による図形を別記事「ジュリア集合」でも紹介していますが、少しジュリア集合の算出方法が異なるものになっています。

Contents

1 ジュリア集合２
- 1.1 ジュリア集合の考え方
- 1.2 プログラムコード

今回描いたジュリア集合による作品は以下の図形となります。

ジュリア集合の考え方

ここでのジュリア集合は、複素平面上の点の集まりで、複素数\(c\)を固定して漸化式\[ z_{n+1} \mapsto \sqrt{z_n-c} \ \ (n=0,1,2,\cdots) \]で定義される複素数列を考えたときに\(n \to \infty \)の極限での複素数の値の集合となります。なお、複素数の平方根には常に2つの複素数の解が存在するので、漸化式のステップごとに対応する解が２倍に増えていき、\(n \to \infty \)の極限での複素数の値は無限個存在することになります。この無限個の集合がジュリア集合となります。

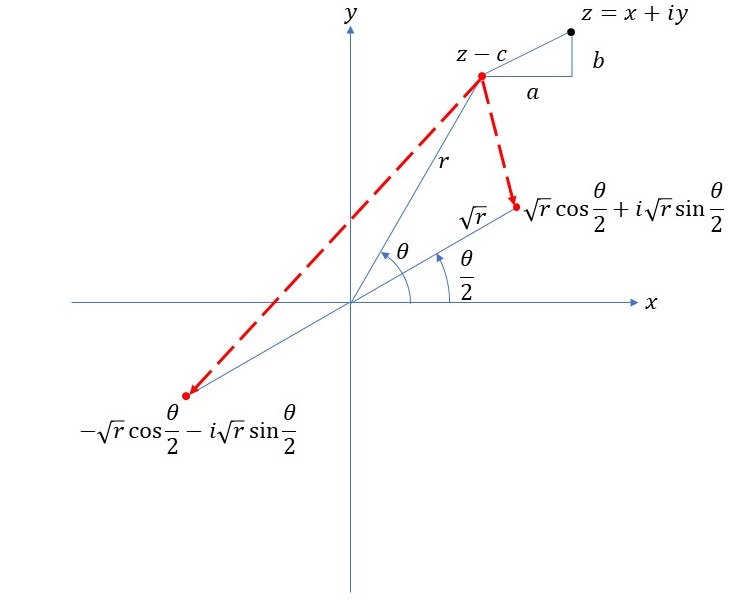
別記事「ジュリア集合」での考え方と比べると、数列を逆方向に扱っているという違いはありますが、結果として出てくる集合は同じものになるはずです。

プログラムコード

このジュリア集合による作品を描いた際のプログラムコード（Processing）を示しておきます。

int iteration_num = 20; // 反復回数 

void setup(){
  size(600,600);
  background(255,255,255);

  // 定数c=a + i b
  float a = 0.3;
  float b = -0.5;
  
  // 描画時のスケール
  float scale = width/4.0;
  // 画像の中心位置
  PVector center = new PVector(width/2.0, height/2.0);
  // 出発点を指定する
  point(center.x+0.1*scale, center.y); 
  
  PImage img;
  float temp_x, temp_y;
  float r, theta;
  int iter = 0;
  while(iter<iteration_num){
    // 描いた図形を一旦imgに保存する
    img = createImage(width, height, RGB);
    loadPixels();
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        img.set(i, j, pixels[j*width + i]);
      }
    }
    background(255,255,255); // キャンバスを白色で塗りつぶす
    // imgの画素が白色でない場合、2つの反復変換を行ってジュリア集合を更新していく
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        if(img.get(i,j) != color(255,255,255)){
          temp_x = (i - center.x)/scale-a;
          temp_y = (j - center.y)/scale-b;
          r = sqrt(pow(temp_x,2)+pow(temp_y,2));
          theta = atan2(temp_y, temp_x);
          point(center.x + sqrt(r)*cos(theta/2.0)*scale, center.y + sqrt(r)*sin(theta/2.0)*scale); 
          point(center.x - sqrt(r)*cos(theta/2.0)*scale, center.y - sqrt(r)*sin(theta/2.0)*scale); 
        }
      }
    }
    iter++;
  }
}