ジュリア集合

ここでは、書籍「フラクタルの美　複素力学系のイメージ」のp.189-191に解説されている「実験その１：吸引領域とジュリア集合」を参考にして、初めてのジュリア集合による作品を作ってみました。

Contents

1 ジュリア集合

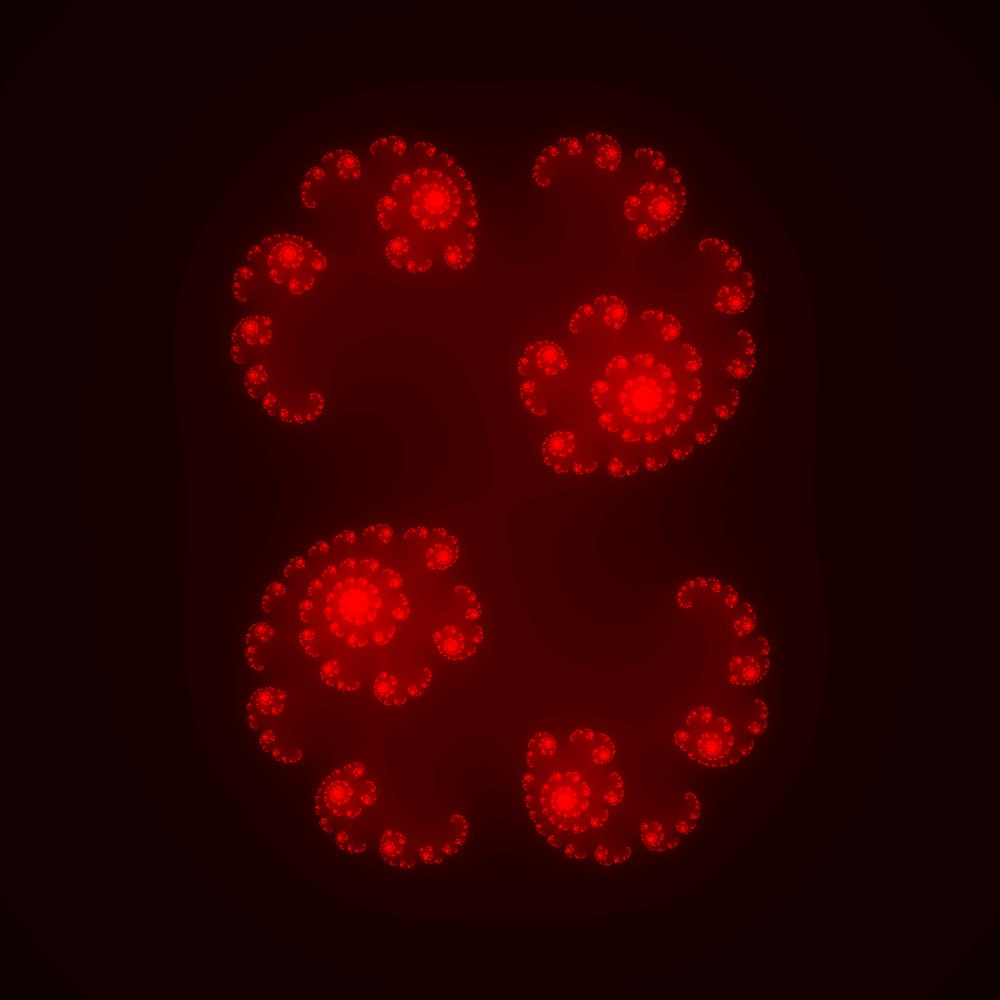
今回描いたジュリア集合による作品は以下の図形となります。

かっこいい図形を描くことができました。

ジュリア集合の考え方

ジュリア集合とは複素平面上の点の集まりで、複素数\( c \)を固定して漸化式

\[ z_{n+1} \mapsto z_n^2 + c \ \ ( n = 0,1,2,\cdots ) \]

で定義される複素数列を考えたときに\( n \to \infty \)の極限で無限大に発散しないという条件を満たす複素数列の初期値\( z_0 \)の全体が作る集合を指します。

このジュリア集合をまともに計算することはできません。そのため、ジュリア集合を用いた図形を描く場合、

\(|z_n|\)はある値\(M\)を越えたときに複素数列は発散したとみなす
\( n \)が適当な上限値\( K \)に達したとき、\(z_K < M\)であれば複素数列は発散しなかったとみなす

として複素数列の初期値\( z_0 \)を分類し、発散したとみなされた場合はそのときの\(n\)の値、発散しなかったとみなされた場合は上限値\(K\)に対応させて、初期値 \( z_0 \) の位置にある画素に色を与えるようにして描いています。

プログラムの流れ

ジュリア集合による作品を作る際のプログラムの流れを記載しておきます。

Step 0

キャンバスサイズ\(w, h\)を決めます。
複素数\(c=p+iq=0.3-0.5i\)、複素平面上の実軸（\(x\)軸）と虚軸（\(y\)軸）の範囲を\(x_\mathrm{min} = y_\mathrm{min} =-1.5, \ \ x_\mathrm{max} = y_\mathrm{max} =1.5 \)、判定条件\(M=200, \ \ K=256 \)を決めます。
\( \Delta x = (x_\mathrm{max} – x_\mathrm{min})/w, \ \ \Delta y = (y_\mathrm{max} – y_\mathrm{min})/h \)とおきます。

以下の処理はキャンバスのすべての画素\((n_x, n_y)\)に対して行います。

Step 1

複素数列の初期値\(x_0=x_\mathrm{min} + n_x \cdot \Delta x, \ \ y_0=y_\mathrm{min} + n_y \cdot \Delta y, \ \ k=0 \)とおきます。

Step 2（反復ステップ）

\((x_k,y_k)\)をもとにして\((x_{k+1},y_{k+1})\)を漸化式

\[ x_{k+1} = x_k^2-y_k^2+p, \ \ y_{k+1}=2x_k y_k + q \]

にしたがって計算します。このとき、カウンター\(k\)の値に\(1\)を加えます。

Step 3（判定ステップ）

\( r = \sqrt{x_k^2+y_k^2} \)を計算します。

(i) \( r>M \)ならば、\(k\)の値に応じてその画素の色を割り当てます。

(ii) \(k=K\)ならば、その画素の色に\(0\)（黒色）を割り当てます。

(iii) \( r \leq M\)かつ\(k<K\)ならば、Step 2に行きます。

プログラムコード

最後に、このジュリア集合による作品を描いた際のプログラムコード（Processing）を示しておきます。

void setup(){
  size(1000,1000);
  
  PImage img = createImage(width, height, RGB);
  
  float p = 0.3; 
  float q = -0.5;
  
  int Kmax = 256;
  float M = 200;
  float xmax = 1.5;
  float xmin = -1.5;
  float ymax = 1.5;
  float ymin = -1.5;
  float delta_x = (xmax - xmin) / width;
  float delta_y = (ymax - ymin) / height;
  
  float x, y, next_x, next_y, r;
  int k;
  for(int i=0; i<width; i++){
    for(int j=0; j<height; j++){
      x = xmin + i * delta_x;
      y = ymax - j * delta_y;
      r = sqrt(x*x+y*y);
      k=0;
      img.set(i,j,color(0,0,0));
      while(k < Kmax){
        if(r > M){
          img.set(i,j,color(10*k,0,0));
          break;
        }
        next_x = x*x - y*y + p;
        next_y = 2.0 * x * y + q;
        x = next_x;
        y = next_y;
        r = sqrt(x*x+y*y);
        k++;
      }
    }
  }
  
  image(img,0,0,width,height);
}