ここでは、書籍「アートで魅せる数学の世界」のp.187-197に掲載されている、反復関数を用いたドラゴン曲線を再現してみました。
Contents
反復関数を用いたドラゴン曲線
まず、反復関数を用いたドラゴン曲線です。

ドラゴン曲線は別記事「Lシステム」でも紹介しています。
ドラゴン曲線に対する反復関数
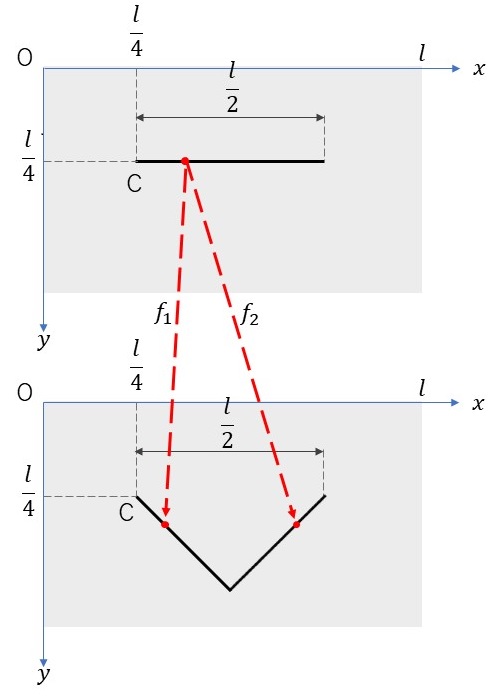
下図のように横の長さが\(l\)となるキャンバス(グレーの領域)に対して\(x\)軸と\(y\)軸をとります。そのキャンバス上に点C\((\frac{l}{4},\frac{l}{4})\)をとり、点Cを左端とする長さ\(\frac{l}{2}\)の線分を取ります。この線分を最初の起点として、ドラゴン曲線を生成するための2つの反復関数は以下のようになります。\[ \begin{align} f_1 &: x \to \frac{1}{2} (x-\frac{l}{4})-\frac{1}{2} (y-\frac{l}{4}) + \frac{l}{4}, \ \ y \to \frac{1}{2} (x-\frac{l}{4})+\frac{1}{2} (y-\frac{l}{4}) + \frac{l}{4} \\ f_2 &: x \to -\frac{1}{2} (x-\frac{l}{4})-\frac{1}{2} (y-\frac{l}{4}) + \frac{3l}{4}, \ \ y \to \frac{1}{2} (x-\frac{l}{4})-\frac{1}{2} (y-\frac{l}{4}) + \frac{l}{4} \end{align} \]
プログラムコード
今回作成した反復関数を用いたドラゴン曲線のプログラムコードを示します。
int iteration_num = 13; // 反復回数
void setup(){
size(600,600);
background(255,255,255);
PVector center = new PVector(width/4.0, height/4.0); // 原点の座標
float len = width/2.0; // 最初に与える線分の長さ
// 直線を描画する
line(center.x, center.y, center.x + len, center.y);
PImage img;
int iter = 0;
while(iter<iteration_num){
// 描いた図形を一旦imgに保存する
img = createImage(width, height, RGB);
loadPixels();
for(int j=0; j<img.height; j++){
for(int i=0; i<img.width; i++){
img.set(i, j, pixels[j*width + i]);
}
}
background(255,255,255); // キャンバスを白色で塗りつぶす
// imgの画素が黒色の場合、2つの反復変換を行ってドラゴン曲線を更新していく
for(int j=0; j<img.height; j++){
for(int i=0; i<img.width; i++){
if(img.get(i,j) == color(0,0,0)){
rect(center.x + 0.5*(i-center.x) - 0.5*(j-center.y), center.y + 0.5*(i-center.x) + 0.5*(j-center.y), 0.1, 0.1);
rect(center.x - 0.5*(i-center.x) - 0.5*(j-center.y) + len, center.y + 0.5*(i-center.x) - 0.5*(j-center.y) , 0.1, 0.1);
}
}
}
iter++;
}
}反復関数を用いたゴールデン・ドラゴン曲線
次は、反復関数を用いたゴールデン・ドラゴン曲線です。
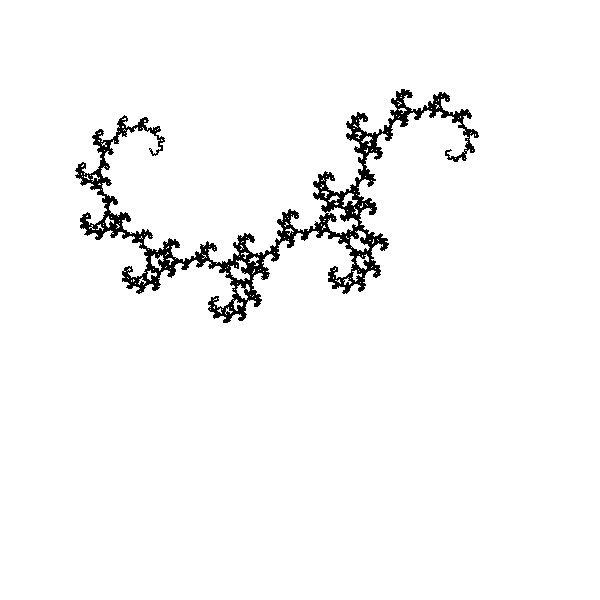
ゴールデン・ドラゴン曲線は書籍「アートで魅せる数学の世界」の裏表紙に掲載されている図形です。
ゴールデン・ドラゴン曲線に対する反復関数
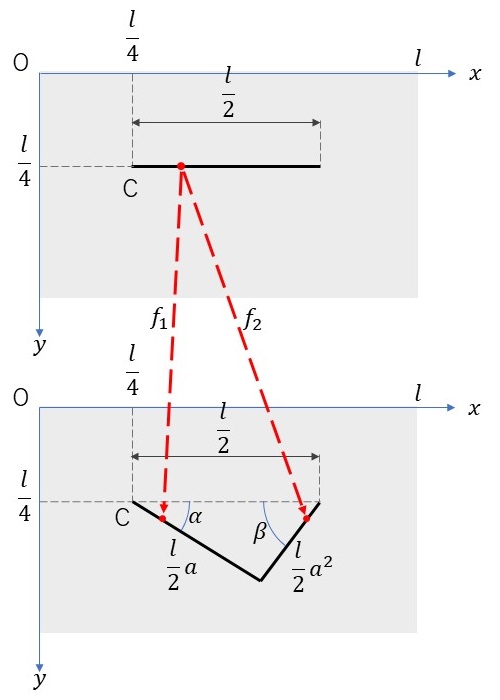
下図のように横の長さが\(l\)となるキャンバス(グレーの領域)に対して\(x\)軸と\(y\)軸をとります。そのキャンバス上に点C\((\frac{l}{4},\frac{l}{4})\)をとり、点Cを左端とする長さ\(\frac{l}{2}\)の線分を取ります。この線分を最初の起点として、ドラゴン曲線を生成するための2つの反復関数は以下のようになります。\[ \begin{align} f_1 &: x \to a \cos \alpha (x-\frac{l}{4})-a \sin \alpha (y-\frac{l}{4}) + \frac{l}{4}, \ \ y \to a \sin \alpha (x-\frac{l}{4})+a \cos \alpha (y-\frac{l}{4}) + \frac{l}{4} \\ f_2 &: x \to -a \cos \beta (x-\frac{l}{4})-a \sin \beta (y-\frac{l}{4}) + \frac{3l}{4}, \ \ y \to a \sin \beta (x-\frac{l}{4})-a \cos \beta (y-\frac{l}{4}) + \frac{l}{4} \end{align} \]また、各パラメータは以下のようになります。\[ \phi = \frac{1+\sqrt{5}}{2}, \ \ a = \left( \frac{1}{\phi} \right)^{\frac{1}{\phi}}, \\ \cos \alpha = \frac{1+a^2-a^4}{2a}, \ \ \cos \beta = \frac{1-a^2+a^4}{2a^2} \]
プログラムコード
今回作成した反復関数を用いたゴールデン・ドラゴン曲線のプログラムコードを示します。
int iteration_num = 13; // 反復回数
void setup(){
size(600,600);
background(255,255,255);
PVector center = new PVector(width/4.0, height/4.0); // 原点の座標
float len = width/2.0; // 最初に与える線分の長さ
// 直線を描画する
line(center.x, center.y, center.x + len, center.y);
// 変換用のパラメータ
float phi = (1.0+sqrt(5.0))/2.0;
float a = pow(1.0/phi, 1.0/phi);
float cosA = (1.0+pow(a,2.0)-pow(a,4.0))/2.0/a;
float sinA = sqrt(1.0 - pow(cosA,2.0));
float cosB = (1.0-pow(a,2.0)+pow(a,4.0))/2.0/pow(a,2.0);
float sinB = sqrt(1.0 - pow(cosB,2.0));
PImage img;
int iter = 0;
while(iter<iteration_num){
// 描いた図形を一旦imgに保存する
img = createImage(width, height, RGB);
loadPixels();
for(int j=0; j<img.height; j++){
for(int i=0; i<img.width; i++){
img.set(i, j, pixels[j*width + i]);
}
}
background(255,255,255); // キャンバスを白色で塗りつぶす
// imgの画素が黒色の場合、2つの反復変換を行ってゴールデン・ドラゴン曲線を更新していく
for(int j=0; j<img.height; j++){
for(int i=0; i<img.width; i++){
if(img.get(i,j) == color(0,0,0)){
rect(center.x + a*cosA*(i-center.x) - a*sinA*(j-center.y), center.y + a*sinA*(i-center.x) + a*cosA*(j-center.y), 0.1, 0.1);
rect(center.x - a*a*cosB*(i-center.x) - a*a*sinB*(j-center.y) + len, center.y + a*a*sinB*(i-center.x) - a*a*cosB*(j-center.y) , 0.1, 0.1);
}
}
}
iter++;
}
}