ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.14に掲載されている、フォードの円を描いてみました。なお、今回はファレイ和を用いて描いていますが、デカルトの円定理を用いた描き方もあり、こちらは別記事で紹介したいと思います。
フォードの円
今回作成したフォードの円です。
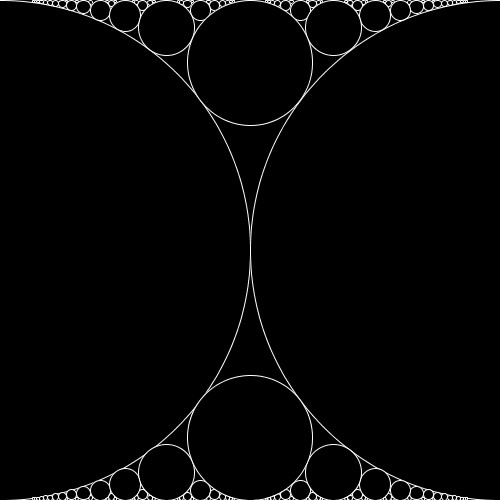
フォードの円の描き方
フォードの円を描くための原理は結構単純です。
- 直線上に、等しい半径の円を2個、互いに接するようにおきます。
- これら2つの円と1つの直線で囲まれた隙間に接する円を描きます。
- 2の過程で描いた円、2の過程の元の2つの円の内の1つと1つの直線で囲まれた隙間に接する円を描きます。
- 3の過程を繰り返すことでフォードの円を描くことができます。
フォードの円の特徴1
フォードの円はすごく面白い特徴を持っています。以下のようにフォードの円の図に対して座標系を取り、図の縦と横の長さが\(1\)となるようにします。
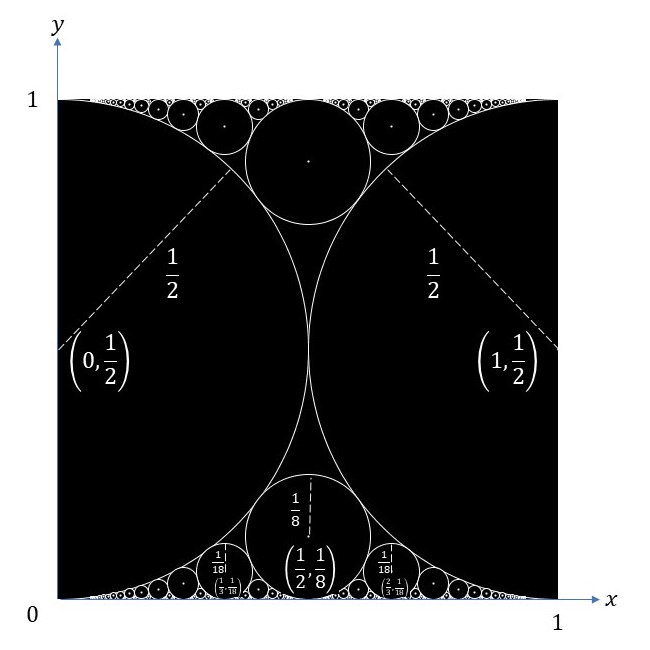
このとき、最初に描く一番大きな2つの円は、半径が\(\frac{1}{2}\)でその中心座標はそれぞれ\((0,\frac{1}{2})\)、\((1,\frac{1}{2})\)となります。
これらの2つの円に接する直線(ここでは\(x\)軸)で囲まれた隙間に接する円を描くと、この円の半径は\(\frac{1}{8}\)でその中心座標は\((\frac{1}{2},\frac{1}{8})\)となります。
次に、半径\(\frac{1}{2}\)、中心座標\((0,\frac{1}{2})\)の円と半径\(\frac{1}{8}\)、中心座標\((\frac{1}{2},\frac{1}{8})\)の円、そして\(x\)軸で囲まれた隙間に接する円を描くと、この円の半径は\(\frac{1}{18}\)でその中心座標は\((\frac{1}{3},\frac{1}{18})\)となります。一方、半径\(\frac{1}{2}\)、中心座標\((1,\frac{1}{2})\)の円と半径\(\frac{1}{8}\)、中心座標\((\frac{1}{2},\frac{1}{8})\)の円、そして\(x\)軸で囲まれた隙間に接する円を描くと、この円の半径は\(\frac{1}{18}\)でその中心座標は\((\frac{2}{3},\frac{1}{18})\)となります。
これらを繰り返していくと、面白い特徴が見えてきます。各円の中心の\(x\)座標を既約分数\(\frac{p}{q}\)で表すと、円は半径\(\frac{1}{2q^2}\)、中心座標\((\frac{p}{q},\frac{1}{2q^2})\)となることがわかります。
フォードの円の特徴2:ファレイ和
また、下図のように円の中心の\(x\)座標の値でラベルを振って眺めてみると、見えてくるものがあります。互いに接する2つの円の中心の\(x\)座標をそれぞれ\(\frac{p_1}{q_1}\)、\(\frac{p_2}{q_2}\)とすると、それらの円と\(x\)軸とで囲まれた隙間に接する円の中心の\(x\)座標の値は\(\frac{p_1+p_2}{q_1+q_2}\)となります。つまり、分母と分子を単純に足した値が隙間に接する円の中心の\(x\)座標になっています。実際、下図のラベルを見ていくと、\[ \frac{0}{1} \oplus \frac{1}{1} = \frac{1}{2}, \ \ \frac{0}{1} \oplus \frac{1}{2} = \frac{1}{3}, \ \ \frac{1}{2} \oplus \frac{1}{1} = \frac{2}{3}, \ \ \frac{0}{1} \oplus \frac{1}{3} = \frac{1}{4}, \ \ \frac{1}{3} \oplus \frac{1}{2} = \frac{2}{5}, \cdots \]となっていることがわかります。
この分母と分子をそれぞれ足した値を「ファレイ和」と呼び、記号\(\oplus\)で表します。
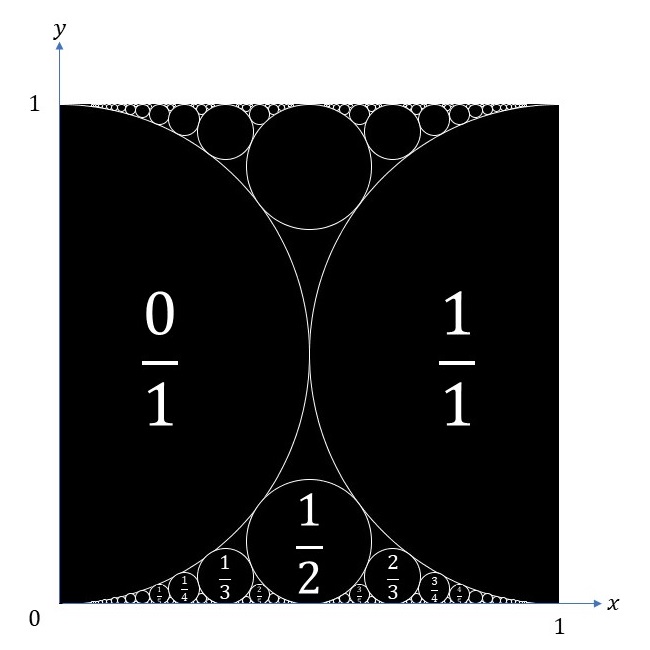
ファレイ和というのはすごく面白いですね。小学生のころ、初めて分数の足し算を習ったとき、分母同士、分子同士を単に足し算して間違いだと言われていたのに、それがファレイ和だと正しいんですから。
プログラムコード
フォードの円を描くプログラムコードを載せておきます。
最初に説明したように、今回はファレイ和を使ってプログラムを作りました。つまり、整数\(p\)と\(q\)を与えて、\((\frac{p}{q}, \frac{1}{2q^2})\)を中心とした半径\(\frac{1}{2q^2}\)の円を描いていくという方法です。
ただし、円を描く順番は\(q\)の値が大きい方から描いています。この理由は、たとえば\(p=1,q=2\)の場合と\(p=2,q=4\)の場合は同じ円になるはずですが、\(q\)の値が小さい方から単純に描いていくと、\(p=1,q=2\)の場合は\((\frac{1}{2}, \frac{1}{8})\)を中心とした半径\(\frac{1}{8}\)の円となり、\(p=2,q=4\)の場合は\((\frac{2}{4}, \frac{1}{32})\)を中心とした半径\(\frac{1}{32}\)の円となるので、\(p=1,q=2\)の円の内部に\(p=2,q=4\)の円が描かれてしまうからです。これは\(\frac{p}{q}\)が既約分数になるように調整してやれば回避できるのですが、今回は円を描く順番を\(q\)の値が大きい方から描くことで、\(p=2,q=4\)の円が\(p=1,q=2\)の円で上書きされるようにして簡易的に回避しました。
void setup(){
size(500,500);
background(0,0,0);
float r_max = width / 2.0; // 円の半径の最大値
float r_min = 1.0; // 円の半径の最小値
float r = r_max; // 円の半径
float x;
stroke(255,255,255); // 円の輪郭は白色
fill(0,0,0); // 円の内部は黒色
circle(0.0, r, 2.0*r); // 最初の大きな円(左)
circle(width, r, 2.0*r); // 最初の大きな円(右)
// ファレイ和を用いてフォードの円を描いていく
int max_q = floor(sqrt(r_max / r_min));
for(int q=max_q; q>1; q--){
for(int p=1; p<q; p++){
x = (float)width * p/q;
r = r_max / pow(q,2);
circle(x, r, 2.0*r);
circle(x, width-r, 2.0*r);
}
}
}