ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.10,11に掲載されていた、平面を充填する曲線の例であるチェザーロ曲線やペアノ=ゴスパー曲線について作ってみました。
チェザーロ曲線
チェザーロ曲線はLシステムで表すと「A+A--A+A:\(\theta\)」となります。\(\theta\)は90°より少し小さい値をとります。以下の図では\(\theta\)を85°にしました。なお、\(\theta\)を60°にすると、コッホ曲線になります。
チェザーロ曲線のステップ
チェザーロ曲線を描く際に、Lシステムの1ステップ前進(A)の部分をさらに「 A+A--A+A:\(\theta\) 」で置き換えていきます。それを図で表すと、以下のようになります。つまり、線分\(P_1P_2\)を図のような同じ長さの線分4本で構成されるパルス図形 \(P_1Q_1Q_2Q_3P_2\) で置き換えていくことでチェザーロ曲線を描くことができます。
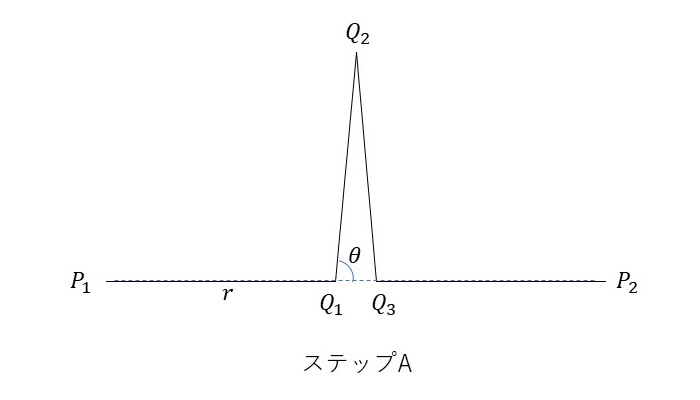
なお、パルス図形に置き換えた際の4本の線分の長さ\(r\)は\[\frac{P_1P_2}{2}=P_1Q_1+Q_1Q_2 \cos \theta \]となることから、\[ r = \frac{l}{2(1+\cos \theta)} \]となります。ここで、線分\(P_1P_2\)の長さを\(l\)とおきました。
プログラムコード
チェザーロ曲線を描くプログラムコードを載せておきます。
float h_min = 5.0; // 枝の長さの最小値
void setup(){
size(500,500);
background(255,255,255);
// チェザーロ曲線
PVector start = new PVector(0.0, height*2.0/3.0);
PVector end = new PVector(width, height*2.0/3.0);
float theta = 85;
drawCesaro(start, end, theta);
}
// チェザーロ曲線を描くための関数
void drawCesaro(PVector start, PVector end, float theta){
// startとendで結ばれる線分を3分割する点
PVector sub_vec = end.copy().sub(start.copy()).mult(1.0/2.0/(1.0+cos(radians(theta))));
PVector sep_point1 = PVector.add(start.copy(), sub_vec.copy());
PVector sep_point2 = PVector.sub(end.copy(), sub_vec.copy());
PVector cesaro_point = PVector.add(sep_point1.copy(), sub_vec.copy().rotate(radians(-theta)));
// チェザーロ曲線を再帰的に描画する
if(sub_vec.mag() > h_min){
drawCesaro(start, sep_point1, theta);
drawCesaro(sep_point1, cesaro_point, theta);
drawCesaro(cesaro_point, sep_point2, theta);
drawCesaro(sep_point2, end, theta);
} else {
line(start.x, start.y, sep_point1.x, sep_point1.y);
line(sep_point1.x, sep_point1.y, cesaro_point.x, cesaro_point.y);
line(cesaro_point.x, cesaro_point.y, sep_point2.x, sep_point2.y);
line(sep_point2.x, sep_point2.y, end.x, end.y);
}
} ペアノ=ゴスパー曲線
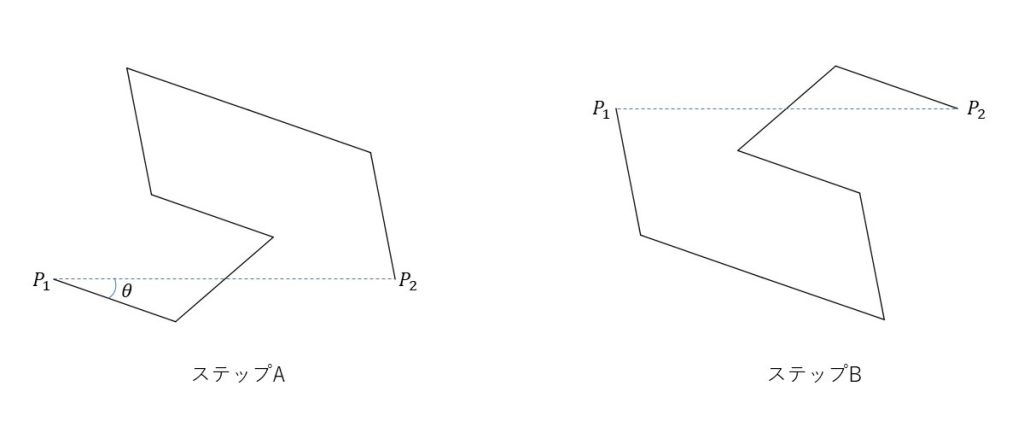
ペアノ=ゴスパー曲線はLシステムで表すと「A+B++B-A--AA-B+:60°」となります。ただし、Aの部分は「A+B++B-A--AA-B+:60°」で置き換えますが、Bの部分は「-A+BB++B+A--A-B:60°」で置き換えていきます。AもBも「1ステップ前進」ではありますが、置き換え方が変わるので区別しています。

ペアノ=ゴスパー曲線のステップ
ペアノ=ゴスパー曲線を描く際に、Lシステムの1ステップ前進(A)及び(B)の置き換えを図で表すと、以下のようになります。線分\(P_1P_2\)に対する1ステップ前進(A)の置き換えに対し、1ステップ前進(B)の置き換えは逆順になっていることが分かります。
角度\(\theta\)の算出
上図の角度\(\theta\)を求めておきます。この値を算出するために、上記のステップAの図形を少し傾け、図形の中を正三角形で埋めていきます。
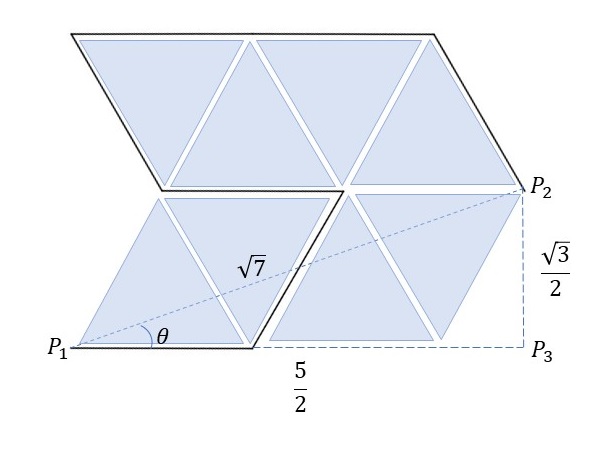
7本の長さが等しい線分(上の長い線分は2本分の線分で構成されている)の長さを1とすると、この図から線分\(P_1P_3\)の長さは\(\frac{5}{2}\)、線分\(P_2P_3\)の長さは\(\frac{\sqrt{3}}{2}\)、そして線分\(P_1P_2\)の長さは\(\sqrt{7}\)となります。したがって、角度\(\theta\)は\[ \theta = \cos^{-1} \left( \frac{5}{2\sqrt{7}} \right) \]などの計算で得られます。
プログラムコード
ペアノ=ゴスパー曲線を描くプログラムコードを載せておきます。
float h_min = 10.0; // 枝の長さの最小値
void setup(){
size(1000,1000);
background(255,255,255);
// 始点と終点を決める
PVector start = new PVector(width/6.0, height*2.0/3.0);
PVector end = new PVector(5.0*width/6.0, height*2.0/3.0);
drawPeanoGosper(start, end);
}
// ペアノ・ゴスパー曲線を描くための関数
void drawPeanoGosper(PVector start, PVector end){
// ペアノ・ゴスパー曲線を描くための点を求める
float theta = acos(5.0/2.0/sqrt(7.0));
PVector sub_vec = end.copy().sub(start.copy()).mult(1.0/sqrt(7.0)).rotate(theta);
PVector point1 = PVector.add(start.copy(), sub_vec.copy());
PVector point2 = PVector.add(point1.copy(), sub_vec.copy().rotate(radians(-60)));
PVector point3 = PVector.add(point2.copy(), sub_vec.copy().rotate(radians(-180)));
PVector point4 = PVector.add(point3.copy(), sub_vec.copy().rotate(radians(-120)));
PVector point5 = PVector.add(point4.copy(), sub_vec.copy());
PVector point6 = PVector.add(point5.copy(), sub_vec.copy());
// ペアノ・ゴスパー曲線を描画する
drawDragon_recurA(start, point1);
drawDragon_recurB(point1, point2);
drawDragon_recurB(point2, point3);
drawDragon_recurA(point3, point4);
drawDragon_recurA(point4, point5);
drawDragon_recurA(point5, point6);
drawDragon_recurB(point6, end);
}
// ペアノ・ゴスパー曲線を描く際、再帰的に呼び出す関数A
void drawDragon_recurA(PVector start, PVector end){
// ペアノ・ゴスパー曲線を描くための点を求める
float theta = acos(5.0/2.0/sqrt(7.0));
PVector sub_vec = end.copy().sub(start.copy()).mult(1.0/sqrt(7.0)).rotate(theta);
PVector point1 = PVector.add(start.copy(), sub_vec.copy());
PVector point2 = PVector.add(point1.copy(), sub_vec.copy().rotate(radians(-60)));
PVector point3 = PVector.add(point2.copy(), sub_vec.copy().rotate(radians(-180)));
PVector point4 = PVector.add(point3.copy(), sub_vec.copy().rotate(radians(-120)));
PVector point5 = PVector.add(point4.copy(), sub_vec.copy());
PVector point6 = PVector.add(point5.copy(), sub_vec.copy());
// ペアノ・ゴスパー曲線を再帰的に描画する
if(sub_vec.mag() > h_min){
drawDragon_recurA(start, point1);
drawDragon_recurB(point1, point2);
drawDragon_recurB(point2, point3);
drawDragon_recurA(point3, point4);
drawDragon_recurA(point4, point5);
drawDragon_recurA(point5, point6);
drawDragon_recurB(point6, end);
} else {
line(start.x, start.y, point1.x, point1.y);
line(point1.x, point1.y, point2.x, point2.y);
line(point2.x, point2.y, point3.x, point3.y);
line(point3.x, point3.y, point4.x, point4.y);
line(point4.x, point4.y, point5.x, point5.y);
line(point5.x, point5.y, point6.x, point6.y);
line(point6.x, point6.y, end.x, end.y);
}
}
// ペアノ・ゴスパー曲線を描く際、再帰的に呼び出す関数B
void drawDragon_recurB(PVector start, PVector end){
// ペアノ・ゴスパー曲線を描くための点を求める
float theta = acos(5.0/2.0/sqrt(7.0));
PVector sub_vec = end.copy().sub(start.copy()).mult(1.0/sqrt(7.0)).rotate(theta);
PVector point1 = PVector.add(start.copy(), sub_vec.copy().rotate(radians(60)));
PVector point2 = PVector.add(point1.copy(), sub_vec.copy());
PVector point3 = PVector.add(point2.copy(), sub_vec.copy());
PVector point4 = PVector.add(point3.copy(), sub_vec.copy().rotate(radians(-120)));
PVector point5 = PVector.add(point4.copy(), sub_vec.copy().rotate(radians(-180)));
PVector point6 = PVector.add(point5.copy(), sub_vec.copy().rotate(radians(-60)));
// ペアノ・ゴスパー曲線を再帰的に描画する
if(sub_vec.mag() > h_min){
drawDragon_recurA(start, point1);
drawDragon_recurB(point1, point2);
drawDragon_recurB(point2, point3);
drawDragon_recurB(point3, point4);
drawDragon_recurA(point4, point5);
drawDragon_recurA(point5, point6);
drawDragon_recurB(point6, end);
} else {
line(start.x, start.y, point1.x, point1.y);
line(point1.x, point1.y, point2.x, point2.y);
line(point2.x, point2.y, point3.x, point3.y);
line(point3.x, point3.y, point4.x, point4.y);
line(point4.x, point4.y, point5.x, point5.y);
line(point5.x, point5.y, point6.x, point6.y);
line(point6.x, point6.y, end.x, end.y);
}
}