バーンズリーのシダ

ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形アルケミスト双書」のp.20,21に掲載されている、バーンズリーのシダを描いてみました。

Contents

1 バーンズリーのシダ

今回描いたバーンズリーのシダです。

バーンズリーのシダは、キャンバス上に種となる1点を描いただけで、後は4つの反復関数を繰り返していけば描けるというものです。たった1点からスタートしてこのような葉っぱの絵が描けるなんてすごいと思いませんか！

バーンズリーのシダに対する反復関数

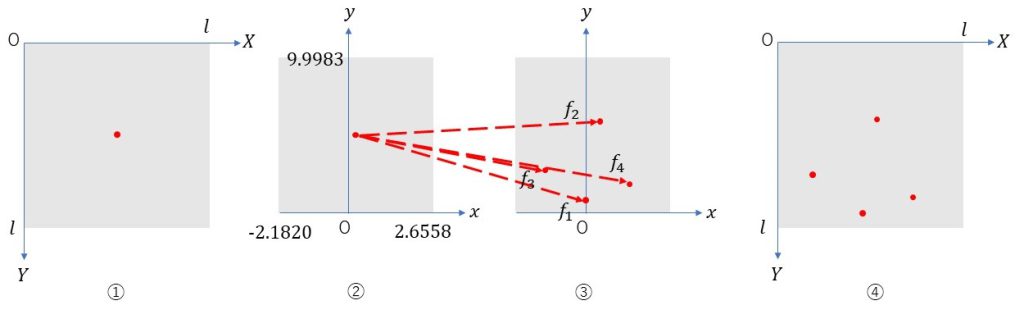
下図②や③のように\(x\)軸と\(y\)軸をとり、描画キャンバスが\(x\)軸方向に\(-2.1820\)から\(2.6558\)、\(y\)軸方向に\(0\)から\(9.9983\)の間となるように設定します。このとき、バーンズリーのシダを生成するための4つの反復関数は以下のようになります。\[ \begin{align} f_1 &: x \to 0, \ \ y \to 0.16y \\ f_2 &: x \to 0.85x+0.04y, \ \ y \to -0.04x+0.85y+1.6 \\ f_3 &: x \to 0.20x-0.26y, \ \ y \to 0.23x+0.22y+1.6 \\ f_4 &: x \to -0.15x+0.28y, \ \ y \to 0.26x+0.24y+0.44 \end{align} \]

ただし、反復関数を利用する座標系\(xy\)（図②と③）と実際の描画キャンバスに定義される座標系\(XY\)（図①と④）は異なっているので、注意が必要です。描画の順番としては、まず図①の\((X,Y)\)座標から図②の\((x,y)\)座標への変換を行います。\[x = -2.1820+\frac{2.6558-(-2.1820)}{l} X, \ \ y = 9.9983-\frac{9.9983}{l} Y \]その後、図②から図③にかけて上記の反復関数を適応した後、図③の\((x,y)\)座標から図④の\((X,Y)\)座標への変換を行います。\[ X = \frac{x-(-2.1820)}{2.6558-(-2.1820)} l, \ \ Y = \frac{9.9983-y}{9.9983}l \]

プログラムコード

今回作成したバーンズリーのシダのプログラムコードを示します。

int iteration_num = 25; // 反復回数 

void setup(){
  size(1000,1000);
  background(255,255,255);

  // 画像の種を描く
  point(width/2.0,height/2.0);

  float x, y;
  float x1, y1, x2, y2, x3, y3, x4, y4;
  PImage img;
  int iter = 0;
  while(iter<iteration_num){
    // 描いた図形を一旦imgに保存する
    img = createImage(width, height, RGB);
    loadPixels();
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        img.set(i, j, pixels[j*width + i]);
      }
    }
    background(255,255,255); // キャンバスを白色で塗りつぶす
    // imgの画素が黒色の場合、4つの反復変換を行ってバーンズリーを更新していく
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        if( img.get(i,j) != color(255,255,255) ){
          x = map(i, 0, width, -2.1820, 2.6558);
          y = map(j, height, 0, 0, 9.9983);
          x1 = map(0.0, -2.1820, 2.6558, 0, width);
          y1 = map(0.16*y, 0, 9.9983, height, 0);
          x2 = map(0.85 * x + 0.04 * y, -2.1820, 2.6558, 0, width);
          y2 = map(-0.04 * x + 0.85 * y + 1.6, 0, 9.9983, height, 0);
          x3 = map(0.20 * x - 0.26 * y, -2.1820, 2.6558, 0, width);
          y3 = map(0.23 * x + 0.22 * y + 1.6, 0, 9.9983, height, 0);
          x4 = map(-0.15 * x + 0.28 * y, -2.1820, 2.6558, 0, width);
          y4 = map(0.26 * x + 0.24 * y + 0.44, 0, 9.9983, height, 0);
          point(x1,y1);
          point(x2,y2);
          point(x3,y3);
          point(x4,y4);
        }
      }
    }
    iter++;
  }
}

参考

今回バーンズリーのシダを作成するにあたり、Wikipediaの「バーンズリーのシダ」を参考にしました。反復関数を利用する座標系での描画キャンバスの範囲はこのサイトの値を利用しています。なお、Wikipediaではバーンズリーのシダをちょっと違う形で描いていく方法がかいてありますので、一度試してみると面白いと思います。（Processingでのプログラムコードも載せてあります。）