ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.15に掲載されている、アポロニウスのギャスケットを描いてみました。書籍では4種類のアポロニウスのギャスケットが描かれていますが、そのうち3種類を描いています。
あと、アポロニウスのギャスケットを描くために「デカルトの円定理」を使っています。この「デカルトの円定理」を使って別記事で紹介した「フォードの円」をもう一度描いてみたいと思います。
Contents
アポロニウスのギャスケット
今回作成した3種類のアポロニウスのギャスケットです。
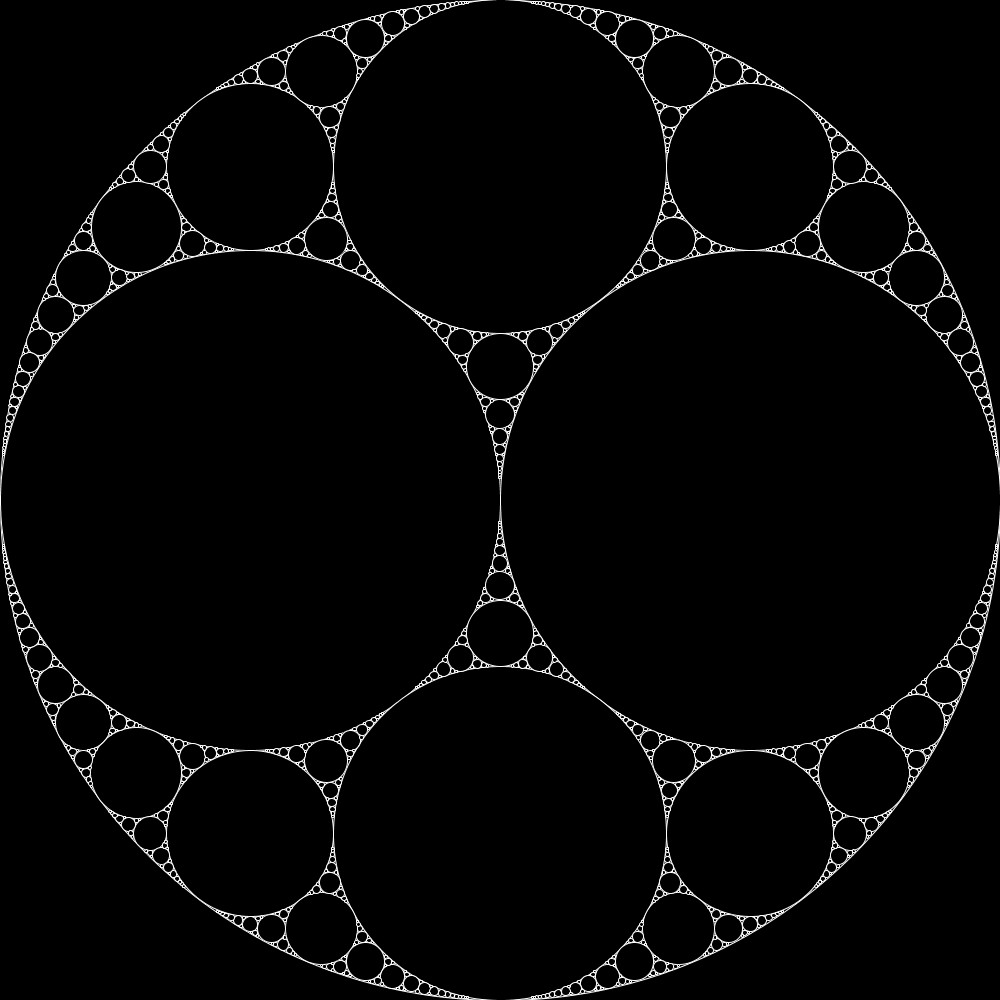
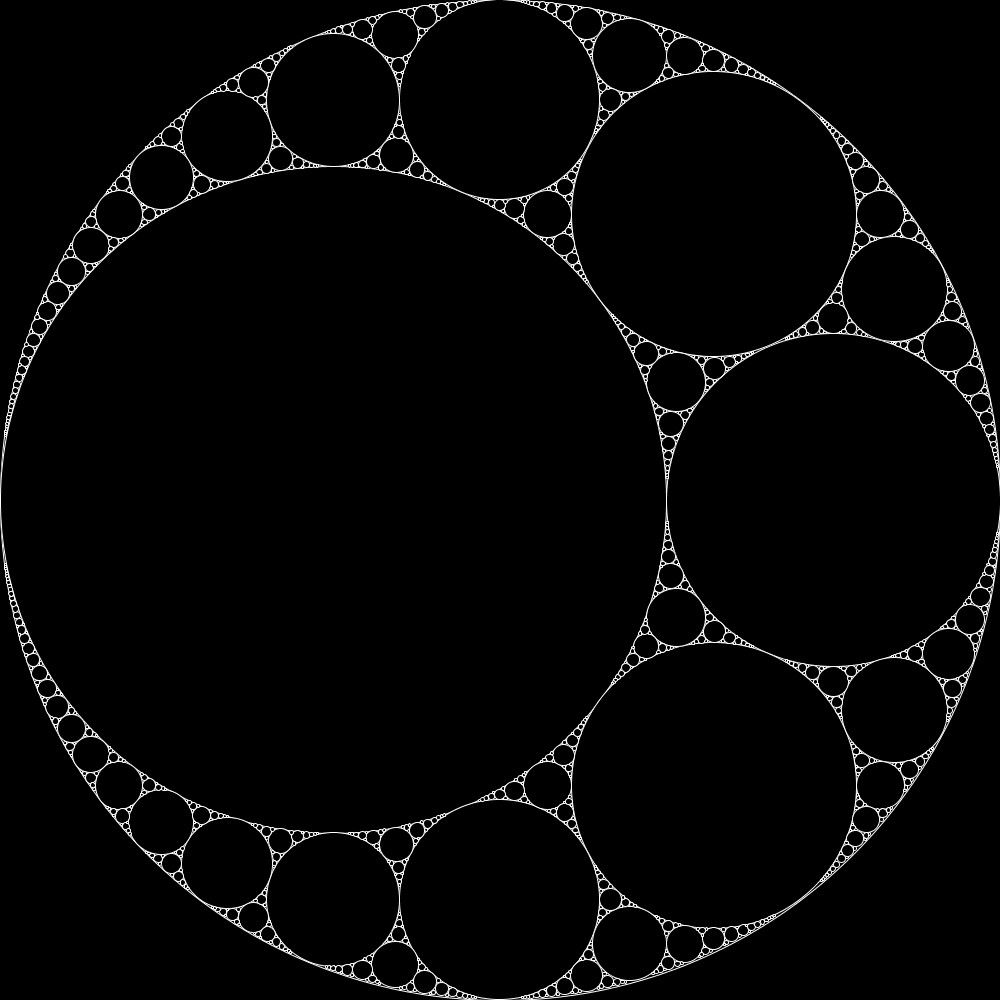
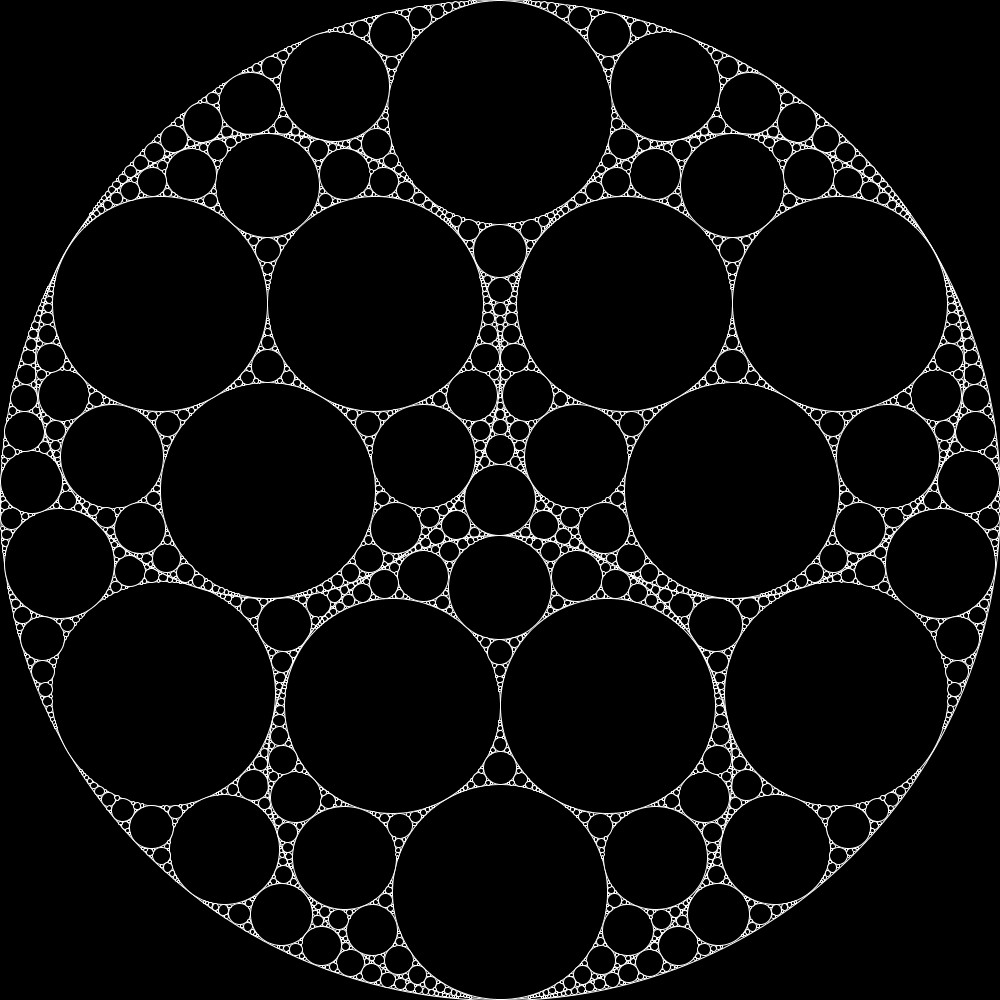
アポロニウスのギャスケットの描き方
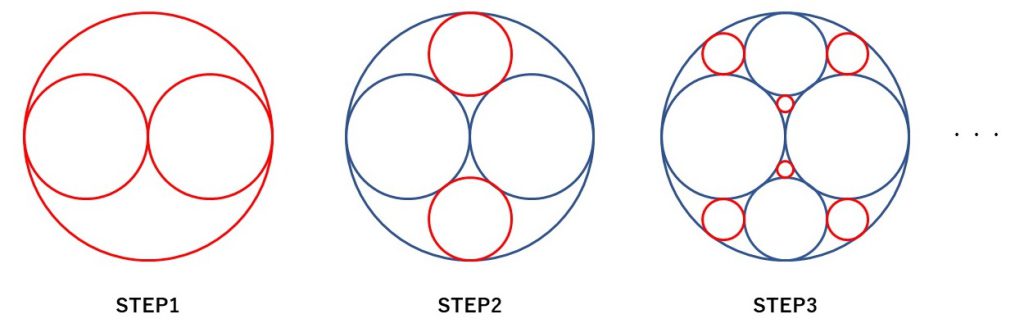
アポロニウスのギャスケットの描き方は、これらの図形を眺めているとなんとなくわかると思います。
- まず大きな円を1つ描き、その円に内接し、かつ互いに外接する2つの円を描きます。
- 次に描いた3つの円の2つの隙間にそれぞれ接する円を描きます。
- さらに描いた5つの円の6つの隙間にそれぞれ接する円を描きます。
- 以降、円の間にできた隙間に接する円を順次描いていくとアポロニウスのギャスケットを描くことができます。
原理的には以上で描くことができるはずですが、実際これらをプログラミングしていくためには、順次描いていく円の半径と中心位置を知る必要があります。これらの円の半径と中心位置はデカルトの円定理を使うことで算出することができます。
デカルトの円定理
まず、円の半径については以下の「デカルトの円定理」を用いることで算出することができます。
定理の主張(半径の算出)
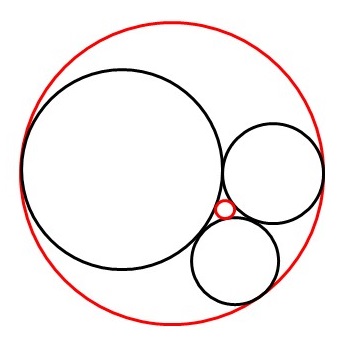
半径\(r\)の円の曲率\(k\)を\(k=\pm \frac{1}{r} \)で定義する。大きな円ほど曲率の絶対値は小さい。\(k\)が正のとき、その円は他の円と外接するものとする(図中の黒い円)。同じく負であるとき、その円は他の円と内接(内包)するものとする(図中の大きな赤い円)。\(k\)が\(0\)のときは、半径が無限に大きな円とみなし、直線を表すものとする。
互いに接する4つの円(もしくは3つの円と1つの直線)の曲率を\(k_1, \ \ k_2, \ \ k_3, \ \ k_4 \)とする。デカルトの定理は、このとき以下の式が成り立つことを主張する。\[(k_1+k_2+k_3+k_4)^2=2(k_1^2+k_2^2+k_3^2+k_4^2) \]先に3つの円(もしくは2つの円と1つの直線)が与えられたとき、4つ目の円の曲率は上式を整理した以下の式で与えられる。\[k_4=k_1+k_2+k_3 \pm 2 \sqrt {k_1k_2+k_2k_3+k_3k_1} \]
複号により解は2つ与えられる。直線への退化を無視すれば、一方の解は常に正で他方は正もしくは負である。負の解は先述したように3つの円を内包する円を表す。
複素数定理(中心位置の算出)
次に、円の中心座標については「複素数定理」を用いることで算出することができます。
以下、円は複素平面上で定義されているものとし、\(j\)番目の円の中心座標\(x_j,y_j)\)を複素数\(z_j=x_j + i y_j\)で表す。このとき、\[ (w_1+w_2+w_3+w_4)^2=2(w_1^2+w_2^2+w_3^2+w_4^2) \] \[ z_4=\frac {w_1+w_2+w_3 \pm 2 \sqrt {w_1w_2+w_2w_3+w_3w_1} }{k_4} \]が成り立つ。ここで\( w_j=k_jz_j\)である。
複号および複素数の平方根の多価性により1つの\(k_4\)に対し2つの解が得られ、そのうちの一方が正しい中心を与える。
以上、「デカルトの円定理」の解説はWikipedia「デカルトの円定理」を参考にしています。
デカルトの円定理を使うときの注意点
大きな円を描き、その円に内接し、かつ互いに外接する2つの円を描くところまで準備してやると、あとはデカルトの円定理を利用して順次、円の半径と中心位置を求めて描いていくことで、アポロニウスのギャスケットを描くことができます。
ただ、デカルトの円定理を利用してアポロニウスのギャスケットを描いていく際にいくつか注意が必要ですので、ここで解説しておきます。
4つ目の円は曲率が大きい方を選択する
デカルトの円定理は、3つの互いに接している円が与えられたとき、4つ目の円の曲率\(k_4\)が\[k_4=k_1+k_2+k_3 \pm 2 \sqrt {k_1k_2+k_2k_3+k_3k_1} \]で与えられることを主張しています。
この性質を使い、描かれた円のうち互いに接する3つの円を選択し、デカルトの円定理を利用して新たな4つ目の円を算出して描いていくということを繰り返していくことでアポロニウスのギャスケットを描いていきます。このとき、選択する3つの円は2つのパターンが考えられます。
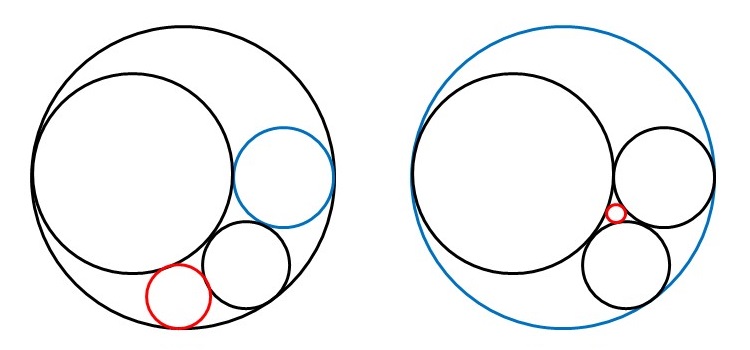
1つ目のパターンは1つの大きな円とそれに内接し、かつ互いに外接する2つの円(左図の3つの黒色の円)が与えられる場合です。この場合は左図のように4つ目の円の候補として赤色の円と青色の円が得られます。今回のアポロニウスのギャスケットを描いていくときの処理の順番を考えると、大きい方の円(青色の円)は最初に与えられているか、すでに描かれていますので、このパターンでは4つ目の円として小さい方の円(赤色の円)を選択します。
2つ目のパターンは3つの円が互いに外接している場合です(右図の3つの黒色の円)。この場合は4つ目の円の候補として3つの円の隙間に接する小さな円(赤色の円)と3つの円が内接する大きな円(青色の円)が得られます。アポロニウスのギャスケットでは他の円が内接する円は最初に与える大きな円以外描かれないので、このパターンでも4つ目の円として小さい方の円(赤色の円)を選択します。
2つのパターンを解説しましたが、どちらのパターンにせよ、4つ目の円として小さい方の円を選択します。曲率は円の半径の逆数で定義されることを考慮すると、半径が小さい円の曲率は大きくなるので、デカルトの円定理で算出された4つ目の円の曲率は\[k_4=k_1+k_2+k_3 + 2 \sqrt {k_1k_2+k_2k_3+k_3k_1} \]を選択します。
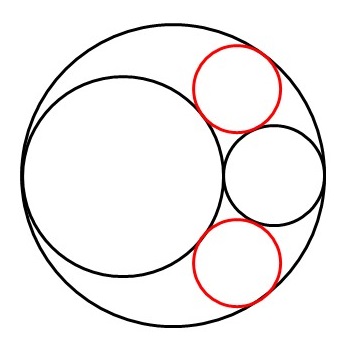
4つ目の円候補の曲率が同じ場合は両方選択する
ただし、4つ目の円としての2つの候補の曲率が同じになる場合があります(下図の2つの赤色の円)。デカルトの円定理では\(k_1k_2+k_2k_3+k_3k_1\)がゼロになる場合です。この場合、2つの候補両方とも選択します。なお、曲率は同じですので、円の中心位置が異なってきます。
正しい中心位置であるか確認する
上記で4つ目の円の曲率を選択したら、次はその中心位置を求めます。中心位置は複素数定理を利用して算出することができますが、その際、定理の但し書きに記載されている『複号および複素数の平方根の多価性により1つの\(k_4\)に対し2つの解が得られ、そのうちの一方が正しい中心を与える。』に注意が必要です。つまり、デカルトの円定理で得られた小さい円の曲率に対して2つの中心位置の候補が存在し、どちらかが正しいのですが、どちらが正しいかを計算して明確に指定することはできないようです。
ただし、プログラミング上はもう少し円の中心位置の候補は増やした方がいいと考えています。というのも、符号の起源が2つあるからです。
1つ目の符号は複素数定理の式\[ z_4=\frac {w_1+w_2+w_3 \pm 2 \sqrt {w_1w_2+w_2w_3+w_3w_1} }{k_4} \]のプラスマイナスの符号です。この符号は方程式\[(w_1+w_2+w_3+w_4)^2=2(w_1^2+w_2^2+w_3^2+w_4^2) \]を\(w_4\)の2次方程式として解いたときに現われます。これは但し書きの中の『復号』に相当する部分になります。
2つ目の符号は、複素数定理の式の\( \sqrt{w_1w_2+w_2w_3+w_3w_1}\)から現れます。つまり、『複素数の平方根の多価性』から来る部分です。\( w_1w_2+w_2w_3+w_3w_1\)の部分をオイラーの公式を利用して\(Re^{i\theta}\)とおくと、\[ \sqrt{w_1w_2+w_2w_3+w_3w_1} = \sqrt{R} e^{i\frac{\theta}{2}} = \sqrt{R} \cos \frac{\theta}{2} + i \sqrt{R} \sin \frac{\theta}{2} \]となります。このとき、\(\cos \frac{\theta}{2} \)と\( \sin \frac{\theta}{2} \)は公式\[ \cos \frac{\theta}{2} = \pm \sqrt{\frac{1+\cos \theta}{2}}, \ \ \sin \frac{\theta}{2} = \pm \sqrt{\frac{1-\cos \theta}{2}} \]で計算されますので、この符号の取り方をどのようにするかがポイントとなってきます。
このような符号の出方のルールはもう少しきちんと見て行けば『1つの\(k_4\)に対し2つの解』になると思いますが、今回はそのルールにはこれ以上立ち入らず、1つの\(k_4\)に対し4つの解の候補、すなわち\(\cos \frac{\theta}{2} \)と\( \sin \frac{\theta}{2} \)を共にゼロ以上の値にとって\[x_4=\frac {x_1+x_2+x_3 \pm 2 \sqrt{R} \cos \frac{\theta}{2} }{k_4}, \ \ y_4=\frac {y_1+y_2+y_3 \pm 2 \sqrt{R} \sin \frac{\theta}{2} }{k_4} \]の復号の4つの組み合わせをすべて試して正しい中心位置を算出するようにしました。
4つの中心位置の候補のうち、正しいものはどれかを確認していきます。この確認方法は曲率を算出したときと同じ、選択する3つの円のパターンで変わってきます。
1つ目のパターン(1つの大きな円とそれに内接し、かつ互いに外接する2つの円)の場合、大きな円の番号を\(1\)とすると、\[ \sqrt{(x_4-x_1)^2+(y_4-y_1)^2} = r_1-r_4, \ \ \sqrt{(x_4-x_2)^2+(y_4-y_2)^2} = r_2+r_4, \ \ \sqrt{(x_4-x_3)^2+(y_4-y_3)^2} = r_3+r_4 \]を満たす\(x_4,y_4\)を選びます。
2つ目のパターン(3つの円が互いに外接している)の場合、\[ \sqrt{(x_4-x_1)^2+(y_4-y_1)^2} = r_1+r_4, \ \ \sqrt{(x_4-x_2)^2+(y_4-y_2)^2} = r_2+r_4, \ \ \sqrt{(x_4-x_3)^2+(y_4-y_3)^2} = r_3+r_4 \]を満たす\(x_4,y_4\)を選びます。
直線の中心位置の扱いについて
ここでは、互いに接している1つの直線と2つの円(下図の黒色の部分)の隙間に接する小さな円(赤色の円)について、その半径と中心位置を算出することを考えます。
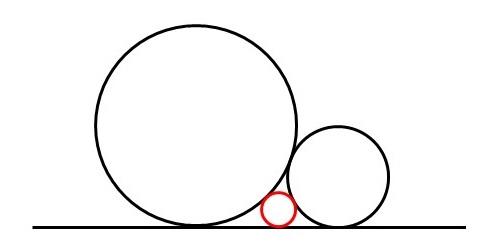
まず、半径についてはデカルトの円定理をそのまま利用します。曲率の説明のところに『\(k\)が\(0\)のときは、半径が無限に大きな円とみなし、直線を表すものとする。』とありますので、今回は直線の曲率を\(k_1=0\)としてデカルトの円定理を利用すると、4つ目の円の曲率\(k_4\)は\[k_4=k_2+k_3 \pm 2 \sqrt{k_2k_3} \]となります。
一方、4つ目の円の中心位置を算出する際は注意が必要です。直線の曲率が\(k_1=0\)のため、複素数定理の式で\(w_1=k_1z_1=0\)とした\[ z_4=\frac {w_2+w_3 \pm 2 \sqrt {w_2w_3} }{k_4} \]で計算すればよさそうに見えますが、これは間違いです。理由は\(w_1\)がゼロではないからです。
これを説明するために、ここで出てくる直線を最初から直線とみなすのではなく、最初は円と考え、その円の半径を無限に大きくしていくことで直線となると考えます。
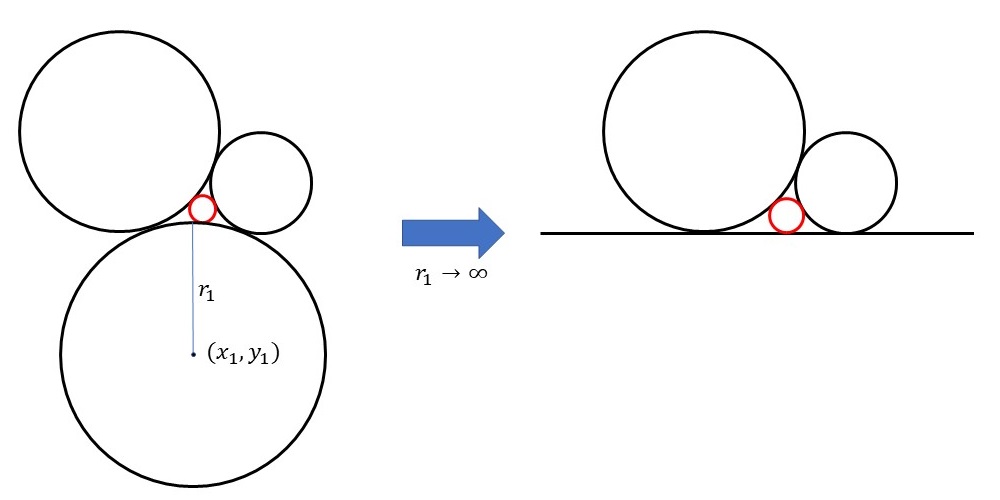
このとき、円の半径を\(r_1\)、中心座標を\(z_1=x_1+iy_1\)とし、他の2つの黒色の円の半径と中心座標をそれぞれ\(r_2, \ \ z_2=x_2+iy_2\)および\(r_3, \ \ z_3=x_3+iy_3\)とおくと、\(r_1\)が十分大きな場合、\[ z_1 \sim z_2+(z_3-z_2) \frac{r_2-r_3+i2\sqrt{r_2r_3}}{(r_2+r_3)^2} (r_1+r_2) \]となり、円の中心座標\(z_1\)は無限に遠くに行くことが分かります。ただ、\(w_1\)は違います。\[w_1=k_1z_1 \sim (z_3-z_2) \frac{r_2-r_3+i2\sqrt{r_2r_3}}{(r_2+r_3)^2} \]となりますので、\(w_1\)の値は有限に残ります。
まとめると、互いに接している1つの直線と2つの円の隙間に接する小さな円の中心座標を求める際、複素数定理を利用しますが、その際の直線に対する\(w_1\)の値は上式で計算した値を利用します。
プログラムコード
上記のデカルトの円定理、およびその利用の際の注意を考慮してアポロニウスのギャスケットを描くためのプログラムコードを紹介します。
アポロニウスのギャスケットを生成する関数
今回、3種類のアポロニウスのギャスケットを描きました。これらに共通して利用するアポロニウスのギャスケットを生成するための関数のプログラムコードです。
使い方として、最初に与える3つの円または1つの直線と2つの円の曲率と中心座標を引数に渡すことでアポロニウスのギャスケットを生成することができます。ただし、内包する円や直線がある場合、その曲率や中心座標は\(k_1\)および\(c1\)に与えるようにします。
// アポロニウスのギャスケットを生成する関数
void drawApollonianGasket(
float k1,
float k2,
float k3,
PVector c1,
PVector c2,
PVector c3
){
// 2つの円の内、曲率が大きい方を描いていく
float k4 = k1+k2+k3+2.0*sqrt(abs(k1*k2+k2*k3+k3*k1));
// 円の位置を算出する準備
PVector w1, w2, w3;
w1 = c1.copy().mult(k1);
w2 = c2.copy().mult(k2);
w3 = c3.copy().mult(k3);
// k1=0のときはw1を更新する
if(abs(k1) < 1.0e-6){
w1.x = (k2*w3.x-k3*w2.x)*(k3-k2)/pow(k3+k2,2.0)
- (k2*w3.y-k3*w2.y)*2.0*sqrt(k2*k3)/pow(k3+k2,2.0);
w1.y = (k2*w3.y-k3*w2.y)*(k3-k2)/pow(k3+k2,2.0)
+ (k2*w3.x-k3*w2.x)*2.0*sqrt(k2*k3)/pow(k3+k2,2.0);
}
float temp_x = (w1.x*w2.x-w1.y*w2.y)
+ (w2.x*w3.x-w2.y*w3.y)
+ (w3.x*w1.x-w3.y*w1.y);
float temp_y = (w1.x*w2.y+w1.y*w2.x)
+ (w2.x*w3.y+w2.y*w3.x)
+ (w3.x*w1.y+w3.y*w1.x);
float temp_size = sqrt(pow(temp_x,2.0)+pow(temp_y,2.0));
float temp_cos = temp_x/temp_size;
// 円の半径がr_minより大きい場合、その円を描く
if(k4 < 1.0/r_min){
PVector c4 = new PVector(0.0,0.0);
float c4_x_sign = 1.0;
float c4_y_sign = 1.0;
float c4_x_re = (w1.x+w2.x+w3.x)/k4;
float c4_x_im = 2.0*sqrt(temp_size)*sqrt((1.0+temp_cos)/2.0)/k4;
float c4_y_re = (w1.y+w2.y+w3.y)/k4;
float c4_y_im = 2.0*sqrt(temp_size)*sqrt((1.0-temp_cos)/2.0)/k4;
float k14_dist = 0.0;
if(k1>1.0e-10){
k14_dist = 1.0/abs(k1) + 1.0/abs(k4);
} else if(k1<-1.0e-10){
k14_dist = 1.0/abs(k1) - 1.0/abs(k4);
}
boolean flag = false;
for(int i=0; i<2; i++){
c4_x_sign = 1.0 - 2.0*i;
for(int j=0; j<2; j++){
c4_y_sign = 1.0 - 2.0*j;
c4.x = c4_x_re + c4_x_sign * c4_x_im;
c4.y = c4_y_re + c4_y_sign * c4_y_im;
if(abs(k1)<1.0e-10){
k14_dist = c4.copy().sub(c1.copy()).mag();
}
if(abs(c4.copy().sub(c1.copy()).mag() - k14_dist ) < 1.0
&& abs(c4.copy().sub(c2.copy()).mag() -1.0/abs(k4) - 1.0/abs(k2) ) < 1.0
&& abs(c4.copy().sub(c3.copy()).mag() -1.0/abs(k4) - 1.0/abs(k3) ) < 1.0
){
flag = true;
break;
}
}
if(flag){break;}
}
circle(c4.x, c4.y, 2.0/k4);
//新たに作った円と元の3つの円のうち2つを組み合わせて再帰的に処理を進める
drawApollonianGasket(k1,k2,k4,c1,c2,c4);
drawApollonianGasket(k2,k3,k4,c2,c3,c4);
drawApollonianGasket(k1,k4,k3,c1,c4,c3);
// もう一つの円がk4と同じ曲率を持つ場合
if(abs(k1*k2+k2*k3+k3*k1) < 1.0e-10){
PVector c4_m = new PVector(0.0,0.0);
c4_m.x = c4_x_re - c4_x_sign * c4_x_im;
c4_m.y = c4_y_re - c4_y_sign * c4_y_im;
circle(c4_m.x, c4_m.y, 2.0/k4);
//新たに作った円と元の3つの円のうち2つを組み合わせて再帰的に処理を進める
drawApollonianGasket(k1,k2,k4,c1,c2,c4_m);
drawApollonianGasket(k2,k3,k4,c2,c3,c4_m);
drawApollonianGasket(k1,k3,k4,c1,c3,c4_m);
}
}
}アポロニウスのギャスケット1
上記で紹介した3つのアポロニウスのギャスケットのうち、1つ目に対するプログラムコードを紹介します。3つの中では一番簡単なものです。大きな円を用意し、その円に内接し、かつ互いに外接する同じ大きさの2つの円を準備し、この3つの円を上記のアポロニウスのギャスケットを生成する関数に設定することで描くことができます。
float r_min = 1.0; // 円の半径の最小値
void setup(){
size(1000,1000);
background(0,0,0);
float r0 = width / 2.0; // 一番外側の円の半径
float r1 = r0/2.0; // 1つ目の円の半径
float r2 = r0/2.0; // 2つ目の円の半径
PVector c0 = new PVector(width/2.0, height/2.0); // 一番外側の円の中心位置
PVector c1 = new PVector(width/4.0, height/2.0); // 1つ目の円の中心位置
PVector c2 = new PVector(width*3.0/4.0, height/2.0); // 2つ目の円の中心位置
stroke(255,255,255);
fill(0,0,0);
circle(c0.x, c0.y, 2.0*r0);
circle(c1.x, c1.y, 2.0*r1);
circle(c2.x, c2.y, 2.0*r2);
float k0 = -1.0/r0; // 一番外側の円の曲率 ※他の円と内接するのでマイナス
float k1 = 1.0/r1; // 1つ目の円の曲率
float k2 = 1.0/r2; // 2つ目の円の曲率
drawApollonianGasket(k0,k1,k2,c0,c1,c2);
}アポロニウスのギャスケット2
上記で紹介した3つのアポロニウスのギャスケットのうち、2つ目に対するプログラムコードを紹介します。1つ目のものと似ています。大きな円を用意し、その円に内接し、かつ互いに外接する2つの円を準備しますが、この2つの円の半径は\(1:2\)になるようにします。これら3つの円を上記のアポロニウスのギャスケットを生成する関数に設定することで描くことができます。
float r_min = 1.0; // 円の半径の最小値
void setup(){
size(1000,1000);
background(0,0,0);
float r0 = width / 2.0; // 一番外側の円の半径
float r1 = r0*2.0/3.0; // 1つ目の円の半径
float r2 = r0/3.0; // 2つ目の円の半径
PVector c0 = new PVector(width/2.0, height/2.0); // 一番外側の円の中心位置
PVector c1 = new PVector(width/3.0, height/2.0); // 1つ目の円の中心位置
PVector c2 = new PVector(width*5.0/6.0, height/2.0); // 2つ目の円の中心位置
stroke(255,255,255);
fill(0,0,0);
circle(c0.x, c0.y, 2.0*r0);
circle(c1.x, c1.y, 2.0*r1);
circle(c2.x, c2.y, 2.0*r2);
float k0 = -1.0/r0; // 一番外側の円の曲率 ※他の円と内接するのでマイナス
float k1 = 1.0/r1; // 1つ目の円の曲率
float k2 = 1.0/r2; // 2つ目の円の曲率
drawApollonianGasket(k0,k1,k2,c0,c1,c2);
}アポロニウスのギャスケット3
上記で紹介した3つのアポロニウスのギャスケットのうち、3つ目に対するプログラムコードを紹介します。大きな円を用意し、その円に内接し、かつ互いに外接する同じ大きさの3つの円を準備します。そして、大きな円と内部の3つの円のうち2つを組み合わせて3パターンの組み合わせを作り、それぞれに上記のアポロニウスのギャスケットを生成する関数に設定することで描くことができます。また、最初に設定した3つの円の内部にもそれぞれアポロニウスのギャスケットが生成されているので、それぞれの円の中にさらに3つの円を用意して、同様の処理を行う必要があります。そのあたりは別途関数としてまとめています。
float r_min = 1.0; // 円の半径の最小値
void setup(){
size(1000,1000);
background(0,0,0);
stroke(255,255,255);
fill(0,0,0);
float r0 = width / 2.0; // 一番外側の円の半径
float r1 = r0*(2.0*sqrt(3.0)-3.0); // 1つ目の円の半径
float r2 = r0*(2.0*sqrt(3.0)-3.0); // 2つ目の円の半径
float r3 = r0*(2.0*sqrt(3.0)-3.0); // 3つ目の円の半径
PVector c0 = new PVector(width/2.0, height/2.0); // 一番外側の円の中心位置
PVector c1 = PVector.fromAngle(radians(-30)).mult(r1*2.0/sqrt(3.0)).add(c0.copy()); // 1つ目の円の中心位置
PVector c2 = PVector.fromAngle(radians(90)).mult(r2*2.0/sqrt(3.0)).add(c0.copy()); // 2つ目の円の中心位置
PVector c3 = PVector.fromAngle(radians(210)).mult(r3*2.0/sqrt(3.0)).add(c0.copy()); // 3つ目の円の中心位置
drawApollonianGasket_circle3(r0,c0);
drawApollonianGasket_circle3(r1,c1);
drawApollonianGasket_circle3(r2,c2);
drawApollonianGasket_circle3(r3,c3);
}
// 1つの大円に対して3つ同じ大きさの内接する円がある場合の
// アポロニウスのギャスケットを描く関数
void drawApollonianGasket_circle3(
float r0, // 一番外側の円の半径
PVector c0 // 一番外側の円の中心位置
){
float r1 = r0*(2.0*sqrt(3.0)-3.0); // 1つ目の円の半径
float r2 = r0*(2.0*sqrt(3.0)-3.0); // 2つ目の円の半径
float r3 = r0*(2.0*sqrt(3.0)-3.0); // 3つ目の円の半径
PVector c1 = PVector.fromAngle(radians(-30)).mult(r1*2.0/sqrt(3.0)).add(c0.copy()); // 1つ目の円の中心位置
PVector c2 = PVector.fromAngle(radians(90)).mult(r2*2.0/sqrt(3.0)).add(c0.copy()); // 2つ目の円の中心位置
PVector c3 = PVector.fromAngle(radians(210)).mult(r3*2.0/sqrt(3.0)).add(c0.copy()); // 3つ目の円の中心位置
circle(c0.x, c0.y, 2.0*r0);
circle(c1.x, c1.y, 2.0*r1);
circle(c2.x, c2.y, 2.0*r2);
circle(c3.x, c3.y, 2.0*r3);
float k0 = -1.0/r0; // 一番外側の円の曲率 ※他の円と内接するのでマイナス
float k1 = 1.0/r1; // 1つ目の円の曲率
float k2 = 1.0/r2; // 2つ目の円の曲率
float k3 = 1.0/r3; // 3つ目の円の曲率
drawApollonianGasket(k0,k1,k2,c0,c1,c2);
drawApollonianGasket(k0,k2,k3,c0,c2,c3);
drawApollonianGasket(k0,k3,k1,c0,c3,c1);
drawApollonianGasket(k1,k2,k3,c1,c2,c3);
} デカルトの円定理を利用したフォードの円
別記事「フォードの円」では、ファレイ和を用いてフォードの円を描きました。ここでは、デカルトの円定理を利用したフォードの円を紹介します。デカルトの円定理を1つの直線とそれに接し、互いにも接する2つの円がある場合に適用した例となります。
なお、直線に対する中心座標は無限遠方になるので、ここではダミーの中心座標をいれており、曲率と中心座標を掛け合わせた値については別途計算するようにしています。
float r_min = 1.0; // 円の半径の最小値
void setup(){
size(500,500);
background(0,0,0);
translate(width/2.0, height/2.0);
stroke(255,255,255);
fill(0,0,0);
float r0 = width / 2.0; // 一番大きい2つの円の半径
PVector c01 = new PVector(-width/2.0, 0.0); // 一番大きい左側の円の中心位置
PVector c02 = new PVector(width/2.0, 0.0); // 一番大きい右側の円の中心位置
circle(c01.x, c01.y, 2.0*r0);
circle(c02.x, c02.y, 2.0*r0);
float k0 = 0.0; // 一つの円は直線のため曲率0
float k1 = 1.0/r0; // 一番大きい左側の円の曲率
float k2 = 1.0/r0; // 一番大きい右側の円の曲率
PVector c_dummy = new PVector(0.0,0.0); // 直線用の中心位置(ダミー)を用意
drawApollonianGasket(k0,k1,k2,c_dummy,c01,c02);
drawApollonianGasket(k0,k2,k1,c_dummy,c02,c01);
}
// アポロニウスのギャスケットを生成する関数
void drawApollonianGasket(
float k1,
float k2,
float k3,
PVector c1,
PVector c2,
PVector c3
){
// 2つの円の内、曲率が大きい方を描いていく
float k4 = k1+k2+k3+2.0*sqrt(abs(k1*k2+k2*k3+k3*k1));
// 円の位置を算出する準備
PVector w1, w2, w3;
w1 = c1.copy().mult(k1);
w2 = c2.copy().mult(k2);
w3 = c3.copy().mult(k3);
// k1=0のときはw1を更新する
if(abs(k1) < 1.0e-6){
w1.x = (k2*w3.x-k3*w2.x)*(k3-k2)/pow(k3+k2,2.0)
- (k2*w3.y-k3*w2.y)*2.0*sqrt(k2*k3)/pow(k3+k2,2.0);
w1.y = (k2*w3.y-k3*w2.y)*(k3-k2)/pow(k3+k2,2.0)
+ (k2*w3.x-k3*w2.x)*2.0*sqrt(k2*k3)/pow(k3+k2,2.0);
}
float temp_x = (w1.x*w2.x-w1.y*w2.y)
+ (w2.x*w3.x-w2.y*w3.y)
+ (w3.x*w1.x-w3.y*w1.y);
float temp_y = (w1.x*w2.y+w1.y*w2.x)
+ (w2.x*w3.y+w2.y*w3.x)
+ (w3.x*w1.y+w3.y*w1.x);
float temp_size = sqrt(pow(temp_x,2.0)+pow(temp_y,2.0));
float temp_cos = temp_x/temp_size;
// 円の半径がr_minより大きい場合、その円を描く
if(k4 < 1.0/r_min){
PVector c4 = new PVector(0.0,0.0);
float c4_x_sign = 1.0;
float c4_y_sign = 1.0;
float c4_x_re = (w1.x+w2.x+w3.x)/k4;
float c4_x_im = 2.0*sqrt(temp_size)*sqrt((1.0+temp_cos)/2.0)/k4;
float c4_y_re = (w1.y+w2.y+w3.y)/k4;
float c4_y_im = 2.0*sqrt(temp_size)*sqrt((1.0-temp_cos)/2.0)/k4;
float k14_dist = 0.0;
if(k1>1.0e-10){
k14_dist = 1.0/abs(k1) + 1.0/abs(k4);
} else if(k1<-1.0e-10){
k14_dist = 1.0/abs(k1) - 1.0/abs(k4);
}
boolean flag = false;
for(int i=0; i<2; i++){
c4_x_sign = 1.0 - 2.0*i;
for(int j=0; j<2; j++){
c4_y_sign = 1.0 - 2.0*j;
c4.x = c4_x_re + c4_x_sign * c4_x_im;
c4.y = c4_y_re + c4_y_sign * c4_y_im;
if(abs(k1)<1.0e-10){
k14_dist = c4.copy().sub(c1.copy()).mag();
}
if(abs(c4.copy().sub(c1.copy()).mag() - k14_dist ) < 1.0
&& abs(c4.copy().sub(c2.copy()).mag() -1.0/abs(k4) - 1.0/abs(k2) ) < 1.0
&& abs(c4.copy().sub(c3.copy()).mag() -1.0/abs(k4) - 1.0/abs(k3) ) < 1.0
){
flag = true;
break;
}
}
if(flag){break;}
}
circle(c4.x, c4.y, 2.0/k4);
//新たに作った円と元の3つの円のうち2つを組み合わせて再帰的に処理を進める
drawApollonianGasket(k1,k2,k4,c1,c2,c4);
// drawApollonianGasket(k2,k3,k4,c2,c3,c4);
drawApollonianGasket(k1,k4,k3,c1,c4,c3);
// もう一つの円がk4と同じ曲率を持つ場合
if(abs(k1*k2+k2*k3+k3*k1) < 1.0e-10){
PVector c4_m = new PVector(0.0,0.0);
c4_m.x = c4_x_re - c4_x_sign * c4_x_im;
c4_m.y = c4_y_re - c4_y_sign * c4_y_im;
circle(c4_m.x, c4_m.y, 2.0/k4);
//新たに作った円と元の3つの円のうち2つを組み合わせて再帰的に処理を進める
drawApollonianGasket(k1,k2,k4,c1,c2,c4_m);
// drawApollonianGasket(k2,k3,k4,c2,c3,c4_m);
drawApollonianGasket(k1,k3,k4,c1,c3,c4_m);
}
}
}