マンデルブロー集合やジュリア集合などなど。フラクタルによる図形はすごく美しい図形です。でも、見ているだけでは物足りない。やっぱり自分でも描いてみたいと思いました。
Contents
ジュリア集合
ここでは、書籍「フラクタルの美 複素力学系のイメージ」のp.189-191に解説されている「実験その1:吸引領域とジュリア集合」を参考にして、ジュリア集合による作品を作ってみました。

ジュリア集合2
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.34,35に掲載されていたジュリア集合による図形を作ってみました。

マンデルブロ集合
ここでは、書籍「フラクタルの美 複素力学系のイメージ」のp.191-192に解説されている「実験その2:マンデルブロー集合」を参考にして、マンデルブロ集合による作品を作ってみました。

樹木
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.2に掲載されていた木構造のフラクタル図形を作ってみました。
コッホ雪片
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.4,5に掲載されていたコッホ雪片を作ってみました。
Lシステム
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.8,9に掲載されているLシステムの例として、レヴィC曲線やドラゴン曲線を作ってみました。

平面を充填する曲線
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.10,11に掲載されていた、平面を充填する曲線の例であるチェザーロ曲線やペアノ=ゴスパー曲線について作ってみました。


カーペット
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.12,13に掲載されている、シェルピンスキーのカーペット、ヴィチェクのカーペット、シェルピンスキーのギャスケット、シェルピンスキーのドイリーを作ってみました。




カーペット2
ここでは、書籍「アートで魅せる数学の世界」のp.170-187で解説されている、パスカルの三角形を用いたシェルピンスキー・ギャスケット、およびデラノイの三角形を用いたシェルピンスキー・カーペットを再現してみました。



フォードの円
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.14に掲載されている、フォードの円を描いてみました。
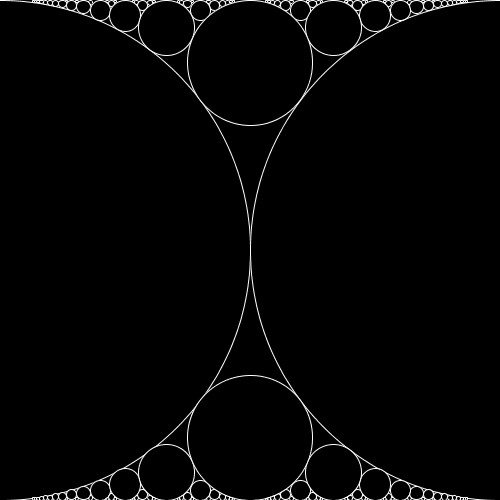
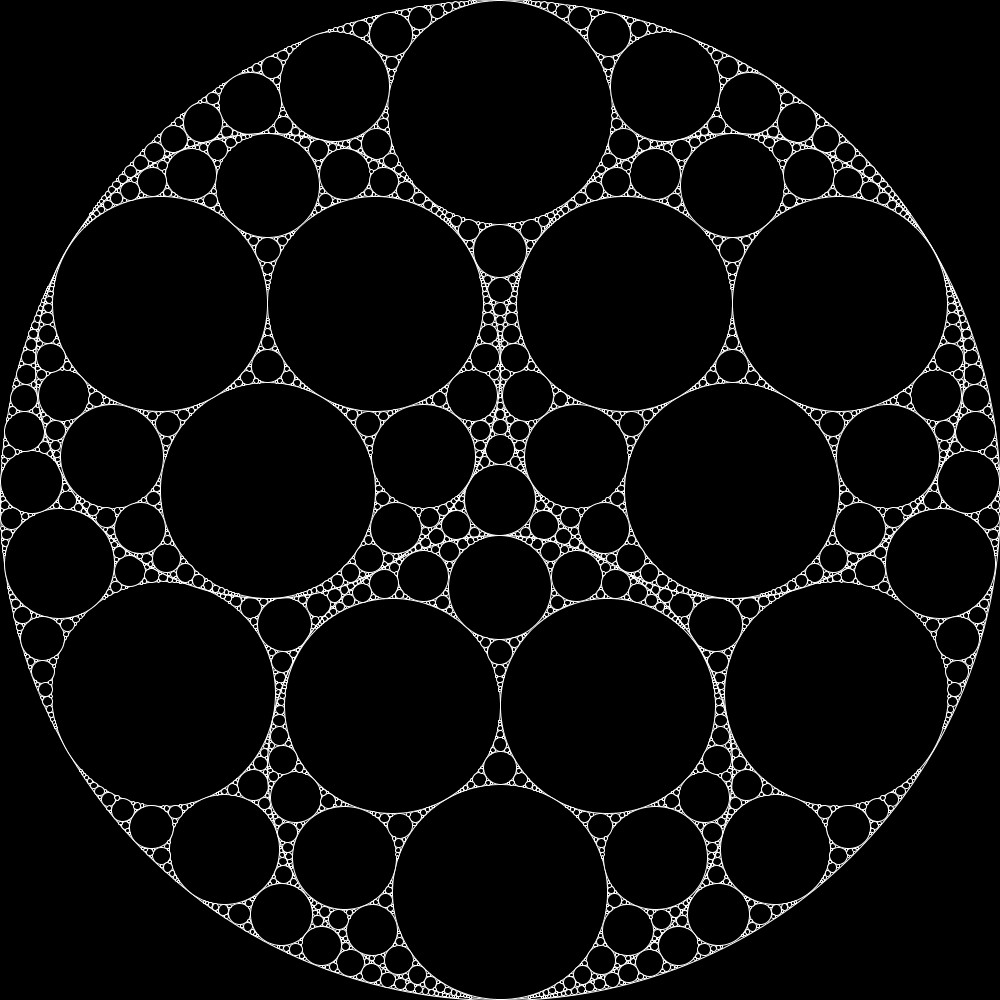
アポロニウスのギャスケット
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.15に掲載されている、アポロニウスのギャスケットを描いてみました。
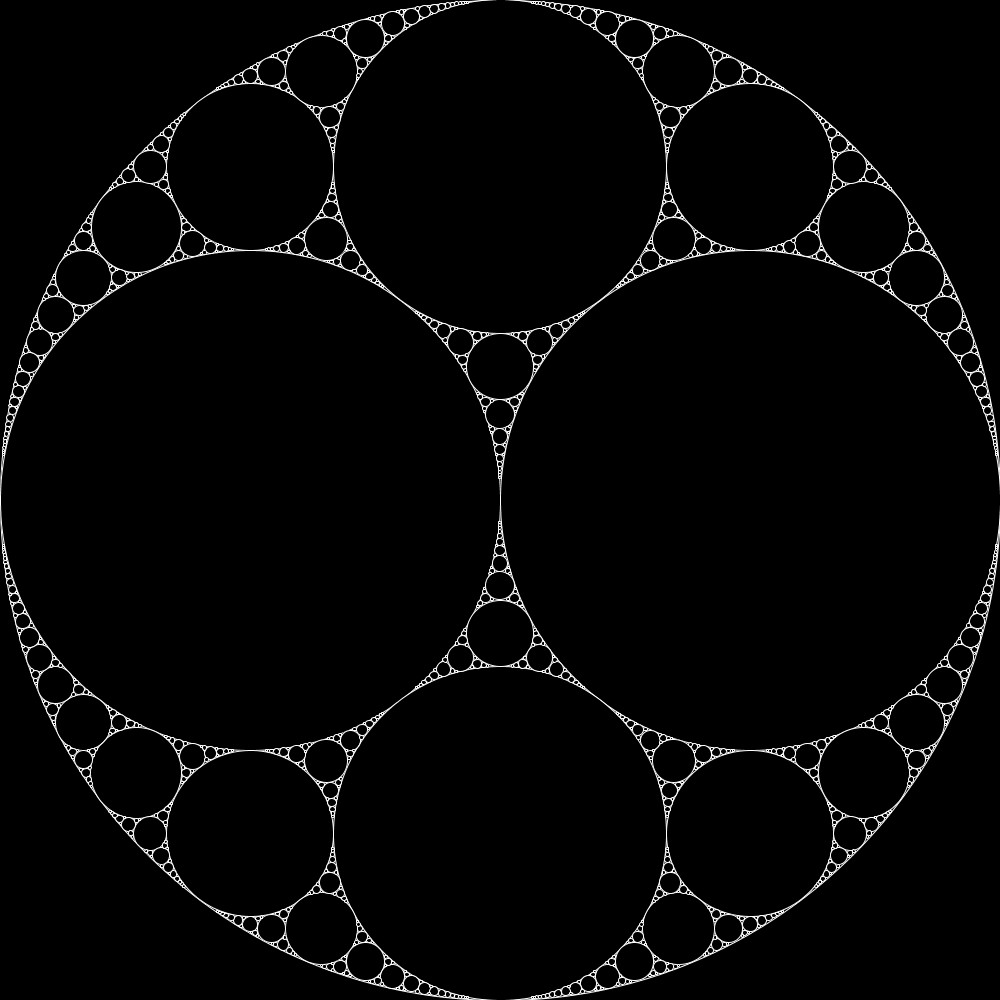
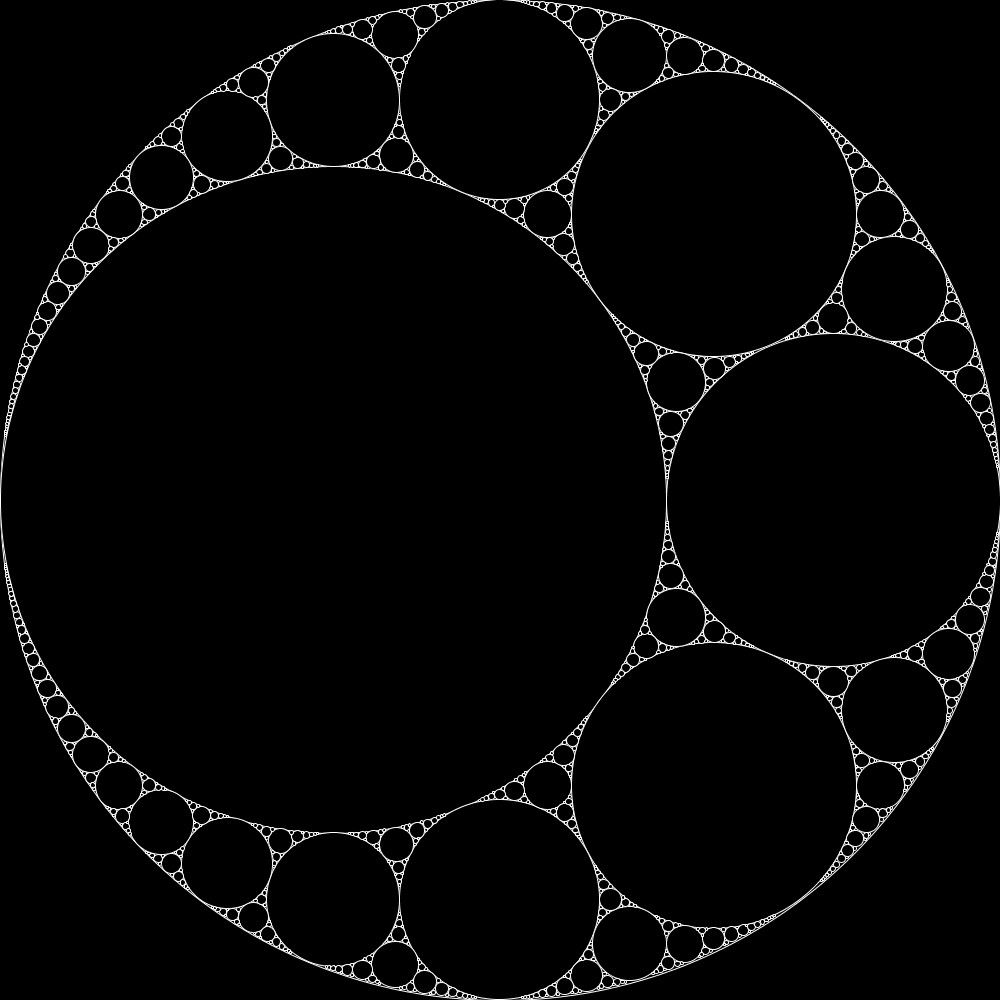
ランダム・ウォーク
ここでは、書籍「アートで魅せる数学の世界」のp.199-203で解説されている、ランダム・ウォークを再現してみました。

レヴィのダスト
ここでは、書籍「アートで魅せる数学の世界」のp.204-205で解説されている、レヴィのダストを再現してみました。

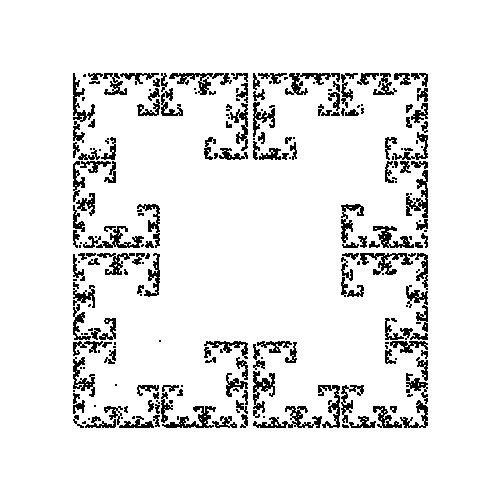
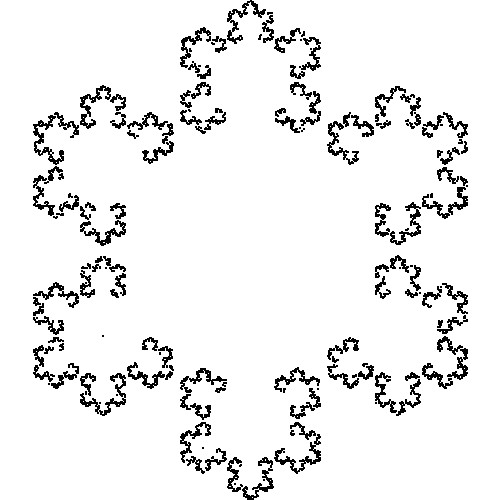
カオスゲーム
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.16,17に掲載されている、カオスゲームと題された6つの図形を再現してみました。




反復関数
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.18,19に掲載されている、反復関数を用いた4つの図形を描いてみました。
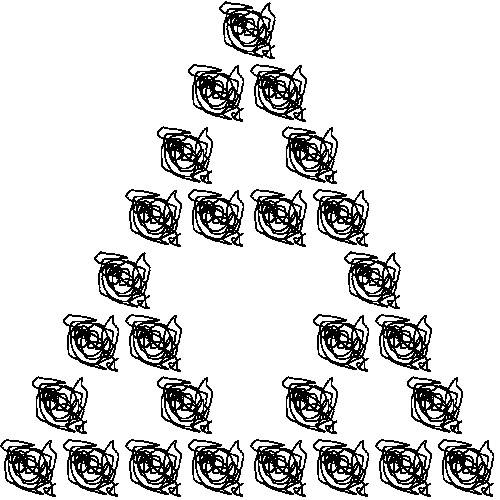



反復関数2
ここでは、書籍「アートで魅せる数学の世界」のp.187-197に掲載されている、反復関数を用いたドラゴン曲線を再現してみました。

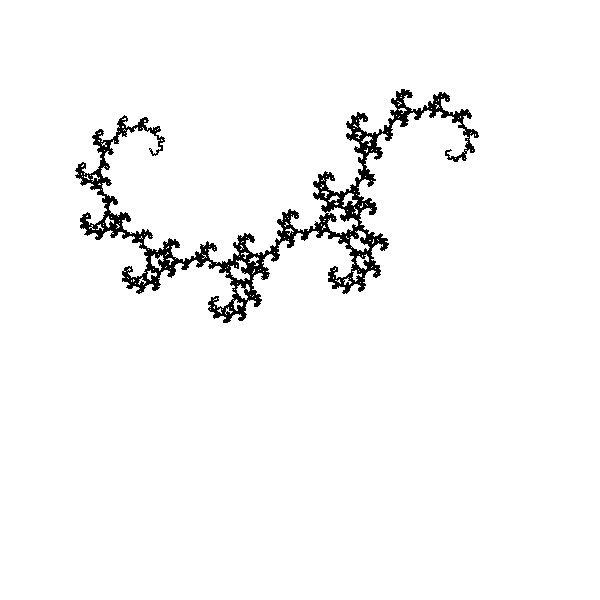
確率的反復関数
ここでは、書籍「アートで魅せる数学の世界」のp.207-209に掲載されている、確率的反復関数を用いたレヴィC曲線とドラゴン曲線を再現してみました。


バーンズリーのシダ
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.20,21に掲載されている、バーンズリーのシダを描いてみました。

非線型変換を含むフラクタル
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.22,23に掲載されている、6つのストレンジアトラクターを再現してみました。






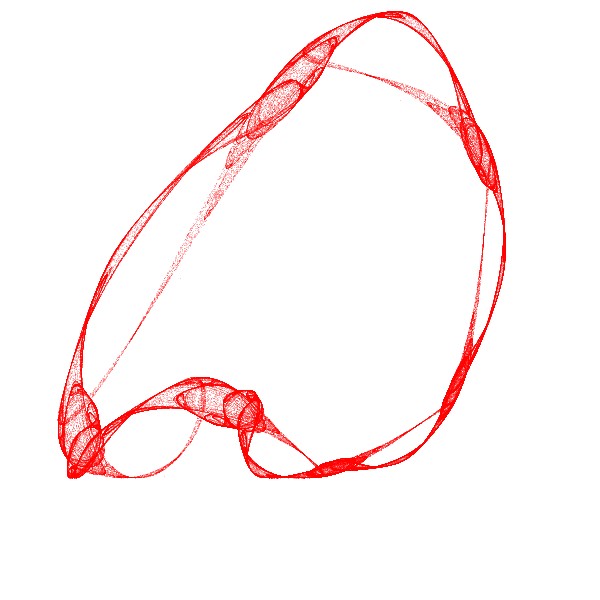
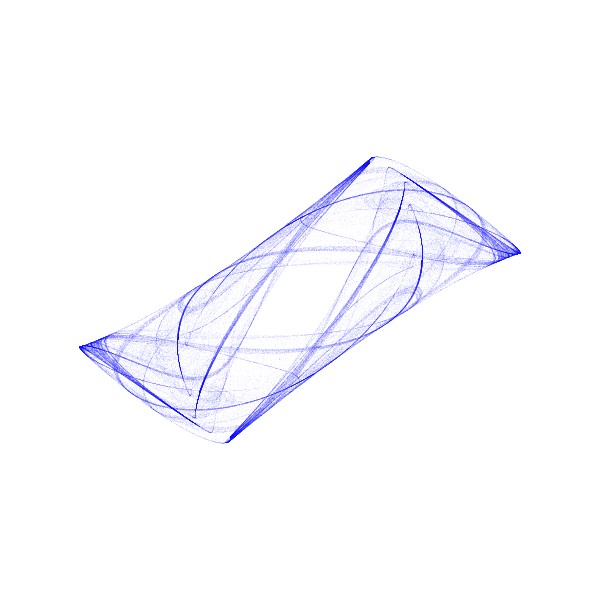
非線型変換を含むフラクタル2
ここでは、書籍「アートで魅せる数学の世界」のp.213-226に掲載されている、ストレンジアトラクターを再現してみました。






ローレンツ・アトラクター
ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.30,31に掲載されている、ローレンツ・アトラクターを再現してみました。


