ここでは、書籍「M.C.エッシャーと楽しむ算数・数学パズル」のp.66-69に紹介されている「ライオンの模様の作図その2」をProcessingで再現してみましたので、その描き方とともに紹介したいと思います。
ライオンの模様その2
今回描いてみたライオンの模様その2は以下のような図形になりました。

描き方
このライオンの模様その2は壁紙群PGGに分類されるものになります。ライオンの模様の基本図形は以下のような形状をしています。
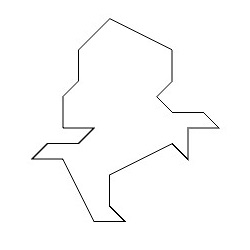
この基本図形を準備することができれば、後はPGG群のルールに従って基本図形を並べていくことでライオンの模様その2を描くことができます。
PGG群の基本図形を選ぶ
ライオンの模様その2の基本図形は、PGG群の基本図形を変形して作成します。そのためにまずPGG群の基本図形を選ぶ必要があります。通常、以前紹介した記事「基本図形の形を考える」の「PGG群の基本図形の形状」の節を参考にして選びます。ただ今回は、書籍「M.C.エッシャーと楽しむ算数・数学パズル」のp.67-68にマス目を利用してライオンの模様その2の基本図形が描かれているので、今回はこのマス目を利用してPGG群の基本図形を以下のように選びました。
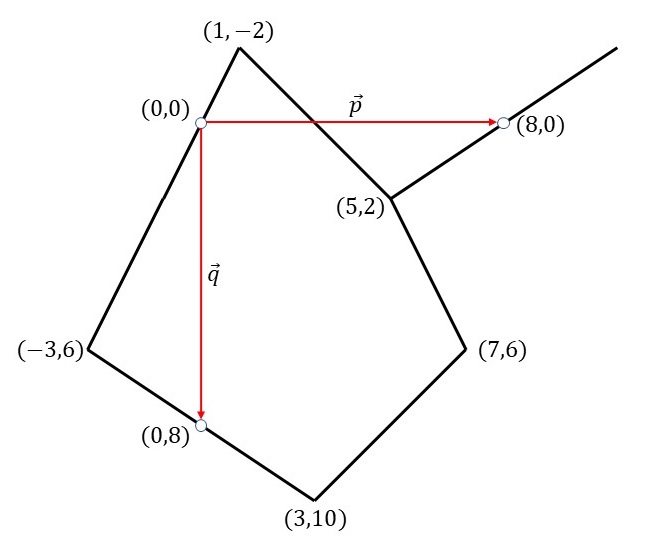
五角形ですが、点\((1,-2)\)と点\((-3,6)\)を結ぶ線分の中点に6番目の角(たまたま180°)があるので、六角形と呼んでいます。
図のように、六角形の辺の一つの中点を原点(0,0)とし、左方向をx軸正の向き、下方向をy軸正の向きとすると、六角形の各頂点や各辺の中点をマス目の座標として表すことができます。
ポイントとしては、\((0,0)\)を長方格子の点とすると、点\((-3,6)\)と点\((3,10)\)とを結ぶ線分の中点\((0,8)\)は隣り合った長方格子の点になることです。つまり、上図の赤い矢印\(\vec{q}\)は長方格子を形づくるための1つのベクトルを表します。また、PGG群の対称性を考慮すると、点\((5,2)\)から右上方向に出た線分は点\((-3,6)\)と点\((3,10)\)とを結ぶ線分をねじれ鏡映で移動させたものになります。その結果、もう一つの赤い矢印\(\vec{p}\)は長方格子を形づくるためのもう1つのベクトルを表すことが分かります。
PGG群の基本図形の変形
PGG群の基本図形を変形するために、隣り合う基本図形同士の辺のラベルと向きをみてみます。
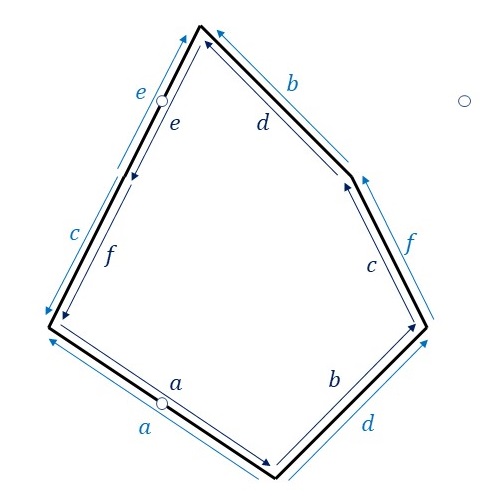
辺\(a\)と辺\(e\)についてはそれぞれ両側のラベルが同じで向きが異なっていますので、中点に関して点対称な変形を行います。一方、辺\(b\)と辺\(d\)、および辺\(c\)と辺\(f\)はそれぞれ同じ向きに重なっています。つまり、辺\(b\)を適当に変形したあと、辺\(d\)は、変形した辺\(b\)を上下反転した形状に変形します。辺\(c\)と辺\(f\)にも同様の変形を行います。そうすると、隣り合う基本図形同士を重ねることなくPGG群の対称性に従って敷き詰めることができます。
実際の変形ですが、今回はマス目を利用して各頂点の座標を指定することで簡単に実現することができます。
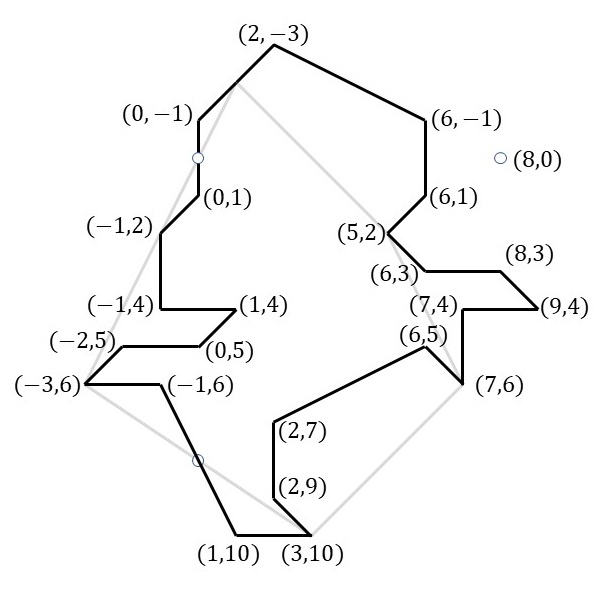
プログラムコード
PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
PVector[] base = new PVector[2]; // 格子を張るベクトル
int col_num = 4; // 描画するタイルの列の数
float scalar; // タイルの辺の長さ
float theta, base_resize;
void setup(){
size(1000, 1000, P2D);
noFill();
scalar = width * 1.0 / col_num; // 描画ウィンドウと行の数からタイルの大きさを決定
makeRectVector(); // 長方格子を張るベクトルの生成
makeLattice(); // 格子点ベクトルを生成
makeTilePGG(); // タイルを生成
drawTiling(); // タイリングを描画
save("PGG_lion.jpg");
}
// 長方格子を張るベクトルを生成する関数
void makeRectVector(){
base[0] = new PVector(8.0, 0.0);
theta = -atan2(base[0].y, base[0].x);
base_resize = 1.0/base[0].mag();
base[0].rotate(theta);
base[0].mult(base_resize);
base[1] = new PVector(0.0,8.0);
base[1].rotate(theta);
base[1].mult(base_resize);
}
// 長方格子を生成する関数
void makeLattice(){
int row_num = ceil(col_num / base[1].y); // 行の数
lattice = new PVector[col_num + 1][row_num + 1];
for (int i = 0; i < col_num + 1; i++){
for (int j = 0; j < row_num + 1; j++){
PVector v = PVector.mult(base[0], i * scalar);
v.add(PVector.mult(base[1], j * scalar));
lattice[i][j] = new PVector(v.x % ((col_num+1)*scalar), v.y);
}
}
}
// 六角形を変形する関数(基本図形)
PShape transformHexagon(){
float[][] v_array = {{-3.0,6.0},{-1.0,6.0},{1.0,10.0},
{3.0,10.0},{2.0,9.0},{2.0,7.0},{6.0,5.0},
{7.0,6.0},{7.0,4.0},{9.0,4.0},{8.0,3.0},{6.0,3.0},
{5.0,2.0},{6.0,1.0},{6.0,-1.0},{2.0,-3.0},{0.0,-1.0},
{0.0,-1.0},{0.0,1.0},
{-1.0,2.0},{-1.0,4.0},{1.0,4.0},{0.0,5.0},{-2.0,5.0}}; // マス目上の頂点
PVector[] v = new PVector[v_array.length]; // 六角形の頂点
PVector center = new PVector(4.0, 4.0); // 基本図形の中心位置
for(int i=0; i<v_array.length; i++){
v[i] = new PVector(v_array[i][0], v_array[i][1]);
v[i].sub(center);
v[i].rotate(theta);
v[i].mult(base_resize * scalar);
}
// 六角形を描く
PShape hexagon = createShape();
hexagon.beginShape();
for(int i=0; i<v_array.length; i++){
hexagon.vertex(v[i].x, v[i].y);
}
hexagon.endShape(CLOSE);
return hexagon;
}
// タイルを生成する関数
void makeTilePGG(){
tile = createShape(GROUP); // PShapeのグループを作る
for(int i=0; i<2; i++){
for(int j=0; j<2; j++){
noStroke();
if( i % 2 == 0 ){
if( j == 0 ){
fill(255,0,0);
} else {
fill(0,255,0);
}
} else {
if( j == 0 ){
fill(0,0,255);
} else {
fill(255,255,0);
}
}
PShape rectangle = transformHexagon(); // 変形した六角形の生成
rectangle.scale(pow(-1,i),pow(-1,j)); // 変形した六角形の反転
rectangle.translate((0.5-j)*scalar, (0.5-i)*scalar*base[1].y); // 変形した六角形の位置を調整
tile.addChild(rectangle); // グループに追加
}
}
}
// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
// background(255);
for (int i=0; i<lattice.length; i++){
for (int j=0; j<lattice[0].length; j++){
if( i%2 == 0 && j%2 == 0 ){
tile.resetMatrix();
tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
shape(tile); // タイルを描画
}
}
}
}