コガネムシの模様

ここでは、書籍「M.C.エッシャーと楽しむ算数・数学パズル」のp.132-137に紹介されている「コガネムシの模様」をProcessingで再現してみましたので、その描き方とともに解説したいと思います。

Contents

1 コガネムシの模様
2 描き方
- 2.1 P4Gの基本図形を選ぶ
- 2.2 P4G群の基本図形の変形
3 プログラムコード

今回描いてみたコガネムシの模様は以下のような図形になりました。

描き方

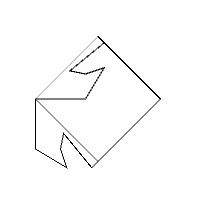
このコガネムシの模様は壁紙群P4Gに分類されるものになります。コガネムシの模様の基本図形は以下のような形状をしています。

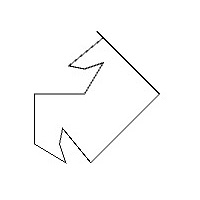
この基本図形を準備することができれば、後はP4G群のルールに従って基本図形を並べていくことでコガネムシの模様を描くことができます。

P4Gの基本図形を選ぶ

コガネムシの模様の基本図形は、P4G群の基本図形を変形して作成します。そのためにまずP4G群の基本図形を選ぶ必要があります。以前紹介した記事「基本図形の形を考える」の「P4G群の基本図形の形状」の節を参考にして、今回は正方形の形状を選びます。

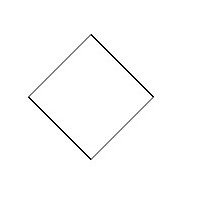
P4G群の基本図形の変形

P4G群の基本図形を変形するために、隣り合う基本図形同士の辺のラベルと向きをみてみます。

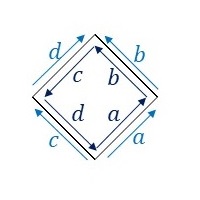
辺\(a,b\)はそれぞれ同じ辺が同じ向きに重なるので、変形できません。一方、辺\(c\)と辺\(d\)は異なる向きに重なっています。つまり、辺\(c\)を自由に変形したものを用意し、それを辺\(d\)の部分に上下左右反対向きに置きます。そうすると、隣り合う基本図形同士を重ねることなくP4G群の対称性に従って敷き詰めることができます。

辺\(c\)と辺\(d\)の変形

辺\(c\)について、今回は以下の図のように変形しています。

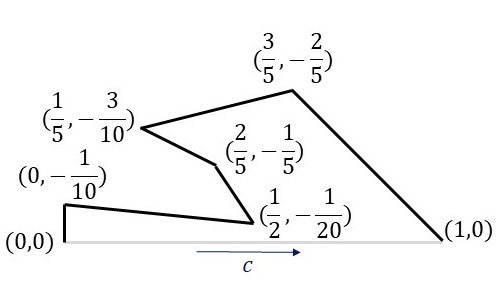
辺\(d\)はこの変形を上下反転したものになります。

この変形を実施した結果、P4G群の基本図形はコガネムシの模様の基本図形に変形することができます。

プログラムコード

P4G群の基本図形を変形した基本図形をP4G群の対称性を考慮して並べていくと、最初に示したような図形を得ることができます。

PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
PVector[] base = new PVector[2]; // 格子を張るベクトル
int col_num = 4; // 描画するタイルの列の数
float scalar; // タイルの辺の長さ

void setup(){
  
  size(1000, 1000, P2D);
  noFill();
  scalar = width * 1.0 / col_num; // 描画ウィンドウと行の数からタイルの大きさを決定
  makeSquareVector(); // 正方格子を張るベクトルの生成
  makeLattice(); // 格子点ベクトルを生成
  makeTileP4G(); // タイルを生成
  drawTiling(); // タイリングを描画
  
  save("P4G_scarab_beetle.jpg");
}

// 正方格子を張るベクトルを生成する関数
void makeSquareVector(){
  base[0] = new PVector(1.0, 0.0);
  base[1] = new PVector(0.0, 1.0);
}

// 正方格子を生成する関数
void makeLattice(){
  int row_num = ceil(col_num / base[1].y); // 行の数
  lattice = new PVector[col_num + 1][row_num + 1];
  for (int i = 0; i < col_num + 1; i++){
    for (int j = 0; j < row_num + 1; j++){
      PVector v = PVector.mult(base[0], i * scalar); 
      v.add(PVector.mult(base[1], j * scalar));
      lattice[i][j] = new PVector(v.x, v.y);
    }
  }
}

// 正方形を変形する関数（基本図形）
PShape transformSquare(){
  
  PVector[] v = new PVector[4]; // 正方形の頂点
  PShape square = createShape();

  v[0] = base[1].copy();
  v[0].mult(scalar / 2.0);
  v[1] = base[0].copy();
  v[1].mult(scalar / 2.0);
  v[2] = base[1].copy();
  v[2].mult(-scalar / 2.0);
  v[3] = base[0].copy();
  v[3].mult(-scalar / 2.0);

  // 正方形を変形する
  square.beginShape(); 
  PVector[] auxiliary_point = new PVector[5];
  // 辺aは変形できず、直線のみ。
  square.vertex(v[0].x, v[0].y);
  square.vertex(v[1].x, v[1].y);
  // 辺bは変形できず、直線のみ。
  square.vertex(v[2].x, v[2].y);
  // 辺cを変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 0.0, -1.0/10.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 5.0/10.0, -0.5/10.0); 
  auxiliary_point[2] = getAuxiliaryPoint(v[2], v[3], 4.0/10.0, -2.0/10.0);
  auxiliary_point[3] = getAuxiliaryPoint(v[2], v[3], 2.0/10.0, -3.0/10.0); 
  auxiliary_point[4] = getAuxiliaryPoint(v[2], v[3], 6.0/10.0, -4.0/10.0);
  for(int i=0; i<5; i++){
    square.vertex(auxiliary_point[i].x, auxiliary_point[i].y);
  }   
  square.vertex(v[3].x, v[3].y);
  // 辺dを辺cと同じ形で逆向きに変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[3], v[0], 4.0/10.0, 4.0/10.0);
  auxiliary_point[1] = getAuxiliaryPoint(v[3], v[0], 8.0/10.0, 3.0/10.0); 
  auxiliary_point[2] = getAuxiliaryPoint(v[3], v[0], 6.0/10.0, 2.0/10.0);
  auxiliary_point[3] = getAuxiliaryPoint(v[3], v[0], 5.0/10.0, 0.5/10.0); 
  auxiliary_point[4] = getAuxiliaryPoint(v[3], v[0], 1.0, 1.0/10.0);
  for(int i=0; i<5; i++){
    square.vertex(auxiliary_point[i].x, auxiliary_point[i].y);
  }
  square.vertex(v[0].x, v[0].y);
  
  square.endShape();
  
  return square;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

// タイルを生成する関数
void makeTileP4G(){
  tile = createShape(GROUP); // PShapeのグループを作る
  for(int j=0; j<2; j++){
    for(int i=0; i<4; i++){

      noStroke();
      if( ( j % 2 == 0 && i % 2 == 0 ) || ( j % 2 == 1 && i % 2 == 1 ) ){
        fill(0,0,0);
      } else {
        fill(255,255,255);
      }   
          
      PShape square = transformSquare(); // 変形した正方形の生成
      square.scale(1, pow(-1,j)); // 正方形の反転
      square.rotate(i*radians(90)); // 正方形の回転
      PVector direction = PVector.fromAngle(i*radians(90)); // 正方形の移動方向
      direction.mult(scalar / 2.0);
      square.translate(direction.x + j*scalar, direction.y + j*scalar); // 正方形の位置を調整
      tile.addChild(square); // グループに追加
    }
  }
}

// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
//  background(255);
  for (int i=0; i<lattice.length; i++){
    for (int j=0; j<lattice[0].length; j++){
      if( i%2 == 0 && j%2==0 ){
        tile.resetMatrix();
        tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
        shape(tile); // タイルを描画 
      }
    }
  }
}