別記事「トカゲの絵を再現してみる」では、エッシャー化の手始めとして、エッシャーの絵で有名なトカゲの絵を再現することを試みました。そこでは、P3群の基本図形として正六角形を選び、各辺を変形することによって、P3群の対称性をみたすようなトカゲの形をした図形を用意し、それを並べていくことで比較的簡単に実現できました。
でも、壁紙アートや壁紙群の知識があり、基本図形の各辺の変形に関しても知識があったとして、実際トカゲの絵のようなものを思いつくことができるでしょうか。正直、エッシャーくらいの才能がないとなかなか難しいと感じます。
この記事では、エッシャーのような天才でなくてもトカゲの絵のようなエッシャー風の絵を描く方法を紹介します。つまり、コンピュータの力を借りれば、私のような凡人でもトカゲの絵のようなものを描くことができます。
なお、ここで紹介する方法は、書籍「エッシャー・マジック―だまし絵の世界を数理で読み解く」の第4章(p.61-72)を参考にしています。
Contents
エッシャー風の絵を描く
今回は、書籍「エッシャー・マジック―だまし絵の世界を数理で読み解く」に例として掲載されている、以下のような牛の図形(元の図形と呼びます)を出発点として、これをP4群の対称性を持つように並べることでエッシャー風の絵を描いてみたいと思います。

ちなみに、今回描いた絵は以下のようになりました。なかなかうまく描けていると思いますが、いかがでしょうか。

エッシャー風の絵を描く手順
ここから、上記のような絵を描いていく方法を紹介していきますが、最初にその手順についてまとめておきたいと思います。
1.元の図形の輪郭を\(n\)角形で近似する
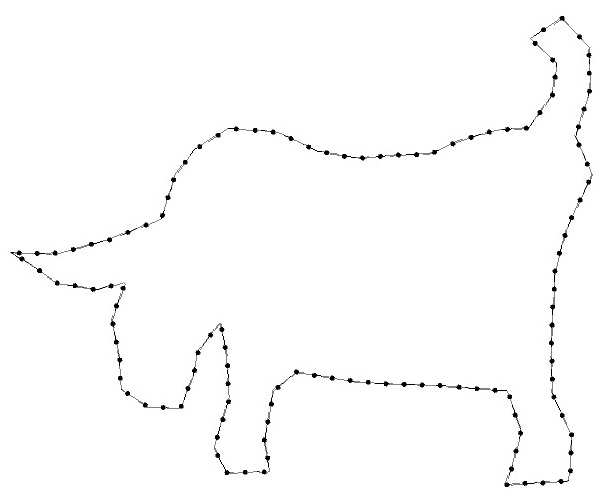
2.壁紙群の基本図形についても\(n\)角形で近似する
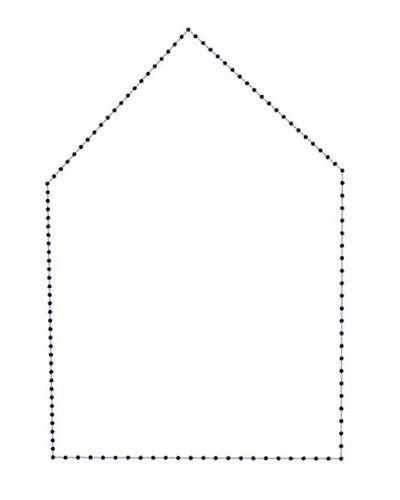
3.元の図形の\(n\)角形とできるだけ同じ形になるように基本図形の\(n\)角形を壁紙群の対称性を保ったまま変形する(赤:元の図形、青:基本図形(変形前)、緑:基本図形(変形後))
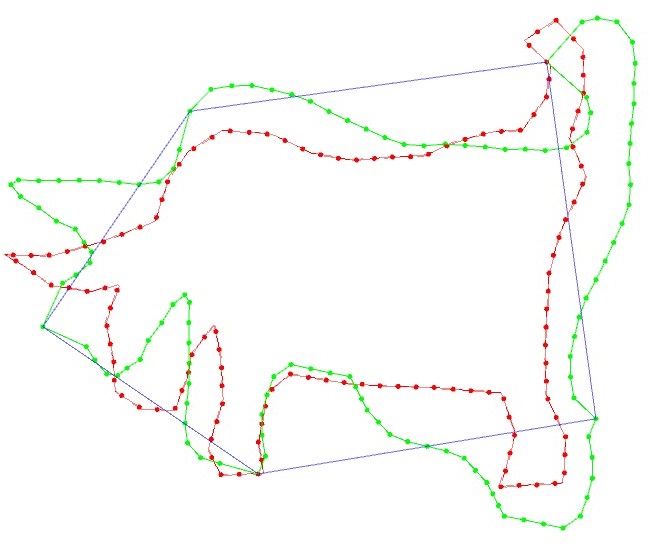
4.変形した基本図形を壁紙群の対称性に合わせて並べていく

元の図形の輪郭を\(n\)角形で近似する
今回、OpenCVの輪郭抽出の機能を利用して、元の図形の輪郭上のすべての点を取得し、これらの輪郭点の集まりから\(n\)個の点をだいたい等間隔になるように選んでいくことで、\(n\)角形の近似を行いました。
元の図形を\(n\)角形で近似する方法について、特定の方法はないです。ただ、2点やっておくことがあります。1つは、画像の左上を原点として右向きを正とする\(x\)座標、下向きを正とする\(y\)座標を取ったときの\(n\)角形の各頂点の位置座標を取得しておくこと、もう1つは元の図形を反時計回りに回るように\(n\)個の頂点に番号を付けておくことです。
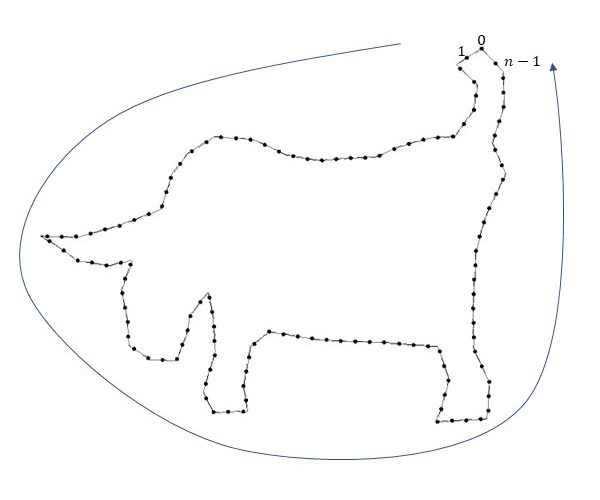
壁紙群の基本図形についても\(n\)角形で近似する
今回はP4群によって並べていきますので、P4群の基本図形を改めて考えてみます。
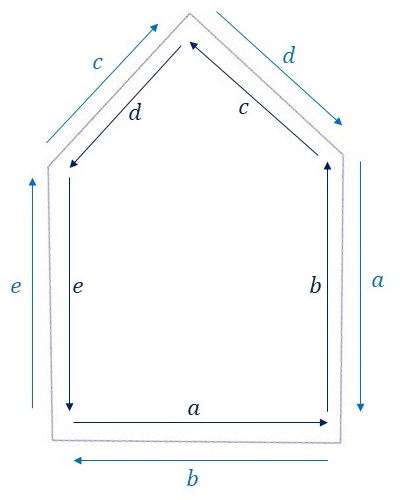
別記事「基本図形の形を考える」において、P4群の基本図形の形状は五角形が許されることがわかりました。上図のように、基本図形の五角形の各辺に\(a,b,c,d,e\)のラベル(濃い青色)を付けると、五角形の性質として、辺\(a\)と辺\(b\)、辺\(c\)と辺\(d\)のそれぞれの長さが等しく、なす角が90°となる形状をもちます。
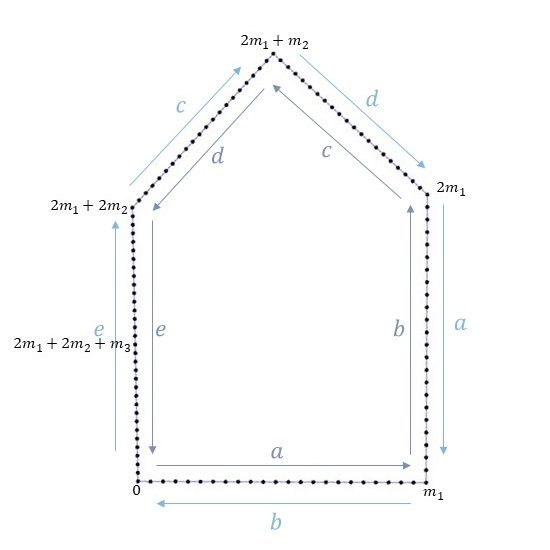
元の図形を\(n\)角形で近似したように、この基本図形についても\(n\)角形に近似します。基本図形の五角形の性質を考慮して、辺\(a\)と辺\(b\)はそれぞれ\(m_1\)個に分割し、辺\(c\)と辺\(d\)はそれぞれ\(m_2\)個に分割、辺\(e\)は\(2m_3\)個に分割します。なお、\(m_1, m_2, m_3\)は\(n=2m_1+2m_2+2m_3\)を満たすように選びます。
そして、反時計回りに下図のように各分割点(\(n\)角形の頂点)に対して番号を振っていきます。
元の図形の\(n\)角形とできるだけ同じ形になるように基本図形の\(n\)角形を壁紙群の対称性を保ったまま変形する
ここから基本図形の変形を考えていきます。
元の図形およびP4群の基本図形をそれぞれ\(n\)角形に近似して頂点に番号を付けました。これらの番号順に\(n\)角形の頂点の座標をそれぞれ\( (\bar{x}_i, \bar{y}_i) \)、\( (x_i, y_i) \)とおきます。そして、次のような値\(F\)を計算します。
\[ F = \sum_{i=0}^{n-1} \{ (x_i-\bar{x}_i)^2 + (y_i-\bar{y}_i)^2 \} \]
この\(F\)は元の図形と基本図形の頂点を順に対応付けし、その頂点同士間の距離の2乗を\(n\)個すべて足していったものになります。この\(F\)の値はすべての\(i\)に対して基本図形の\(n\)角形の頂点位置を調整して、それぞれ対応する元の図形の頂点位置との距離が近いほど、その値は小さくなります。つまり、\(F\)の値が小さいほど、元の図形と変形した基本図形の形状は似てくるというわけです。
この\(F\)が最小になるのは、基本図形の\(n\)角形が元の図形の\(n\)角形と一致するときです。ただ、これでは基本図形がP4群の対称性を満たさないことになります。ここで必要なのは、\(F\)の値をできるだけ小さくしつつ、かつP4群の対称性を満たしながら基本図形を変形していくことです。そこで、基本図形の\(n\)角形の頂点がP4群の対称性を満たすための条件を考えていきます。

別記事「基本図形を変形する」に記載した「変形する際のルール」を用いて、P4群の基本図形である五角形の変形について考えてみます。そのため、P4群の対称性に従って、この五角形を並べていったときに隣り合う図形のどの辺がどの向きに重なるのかを上図に示しています(薄い青色の矢印とラベル)。辺\(a\)と辺\(b\)が異なる向きに重なっていますので、辺\(a\)を自由に変形したものを用意し、それを辺\(b\)の部分に反対向きに置くことでP4群の対称性を保ったまま変形することができます。また、辺\(c\)と辺\(d\)も異なる向きに重なっているので、辺\(c\)と辺\(d\)についても同じように変形できます。一方、辺\(e\)については両側のラベルが同じで向きが異なっていますので、中点に関して点対称な変形を行う必要があります。
以上のことを、基本図形の\(n\)個の頂点で表すと、各頂点に対して以下のような対応関係があることが分かります。
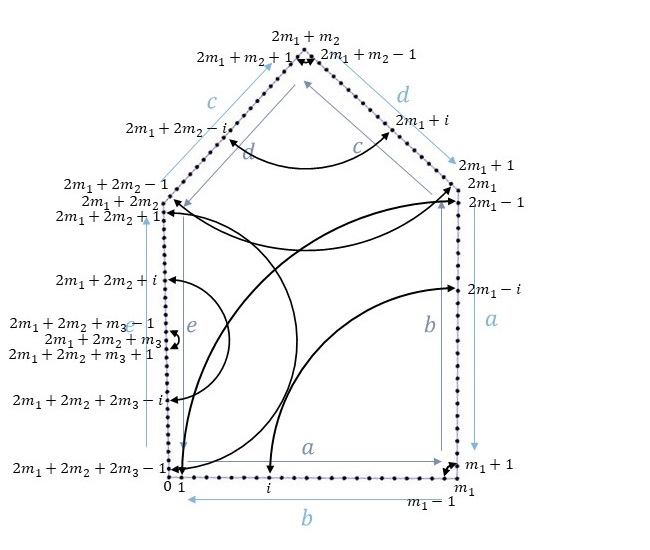
辺\(a\)上の頂点\(i\)は、頂点\(m_1\)を中心として反時計回りに90°回転すると、辺\(b\)上の頂点\(2m_1-i\)に一致します。これを数式で表すと、以下のようになります。
\[ \boldsymbol{x}_{2m_1-i} – \boldsymbol{x}_{m_1} = R_{90} ( \boldsymbol{x}_{i} – \boldsymbol{x}_{m_1} ), \ \ (i = 0, 1, \cdots, m_1-1 ) \]
ここで、\( \boldsymbol{x}_{i} \)は頂点\(i\)の座標位置で、
\[ \boldsymbol{x}_{i} = \left( \begin{array}{c} x_i \\ y_i \\ \end{array} \right) \]
のようにベクトルで表しています。また、\(R_{90}\)はベクトルを反時計回りに90°回転させる回転行列で
\[ R_{90} = \left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \\ \end{array} \right) \]
のように表すことができます。
同様に、辺\(c\)上の頂点\( 2m_1+i \)は、頂点\(2m_1+m_2\)を中心として反時計回りに90°回転すると、辺\(d\)上の頂点\(2m_1+2m_2-i\)に一致します。これを数式で表すと、以下のようになります。
\[ \boldsymbol{x}_{2m_1+2m_2-i} – \boldsymbol{x}_{2m_1+m_2} = R_{90} ( \boldsymbol{x}_{2m_1+i} – \boldsymbol{x}_{2m_1+m_2} ), \ \ (i = 0, 1, \cdots, m_2-1 ) \]
辺\(e\)は中点に関して点対称な変形になるので、辺\(e\)上の頂点\( 2m_1+2m_2+i \)は、頂点\(2m_1+2m_2+m_3\)を中心として反時計回りに180°回転すると、辺\(e\)上の頂点\(2m_1+2m_2+2m_3-i\)に一致します。これを数式で表すと、以下のようになります。
\[ \boldsymbol{x}_{2m_1+2m_2+2m_3-i} – \boldsymbol{x}_{2m_1+2m_2+m_3} = – ( \boldsymbol{x}_{2m_1+2m_2+i} – \boldsymbol{x}_{2m_1+2m_2+m_3} ), \ \ (i = 0, 1, \cdots, m_3-1 ) \]
これらの式は基本図形の\(n\)角形の頂点がP4群の対称性を満たすための条件式となります。得られた式を整理すると、以下のようになります。
\[ \begin{align} \boldsymbol{x}_{m_1+i} &= R_{90} \boldsymbol{x}_{m_1-i}+(1-R_{90}) \boldsymbol{x}_{m_1}, \ \ (i=0,1, \cdots, m_1-1) \\ \boldsymbol{x}_{2m_1} &= R_{90} \boldsymbol{x}_{0}+(1-R_{90}) \boldsymbol{x}_{m_1} \\ \boldsymbol{x}_{2m_1+m_2+i} &= R_{90} \boldsymbol{x}_{2m_1+m_2-i}+(1-R_{90}) \boldsymbol{x}_{2m_1+m_2}, \ \ (i=1, \cdots, m_2-1) \\ \boldsymbol{x}_{2m_1+2m_2} &= – \boldsymbol{x}_{0} + ( 1+R_{90}) \boldsymbol{x}_{m_1}+(1-R_{90}) \boldsymbol{x}_{2m_1+m_2} \\ \boldsymbol{x}_{2m_1+2m_2+m_3} &= \frac{1}{2} \{ ( 1+R_{90}) \boldsymbol{x}_{m_1}+(1-R_{90}) \boldsymbol{x}_{2m_1+m_2} \} \\ \boldsymbol{x}_{2m_1+2m_2+m_3+i} &= (1+R_{90}) \boldsymbol{x}_{m_1}+(1-R_{90}) \boldsymbol{x}_{2m_1+m_2} – \boldsymbol{x}_{2m_1+2m_2+m_3-i}, \ \ (i=1, \cdots, m_3-1) \\ \end{align} \]
これらの条件式を満たしながら、\(F\)の値ができるだけ小さくなるように基本図形の頂点位置を調整していけばいいわけです。
実際に、コンピュータでこの処理を行うために、もう少しこれらの式を整理していきます。基本図形の\(n\)個すべての頂点の座標を並べて、1つの\(2n\)次元のベクトル\(\boldsymbol{u} \)にします。
\[ \boldsymbol{u} = (x_0, y_0, x_1, y_1, \cdots, x_{n-1}, y_{n-1})^t \]
同様に、元の図形の\(n\)角形近似の頂点の座標を並べて、1つの\(2n\)次元のベクトル\(\boldsymbol{w} \)にします。
\[ \boldsymbol{w} = (\bar{x}_0, \bar{y}_0, \bar{x}_1, \bar{y}_1, \cdots, \bar{x}_{n-1}, \bar{y}_{n-1})^t \]
ベクトル\( \boldsymbol{u}, \ \ \boldsymbol{w} \)を利用すると、\(F\)の式は次のように書き直すことができます。
\[ F = (\boldsymbol{u} – \boldsymbol{w})^t \cdot (\boldsymbol{u} – \boldsymbol{w}) \]
また、上で求めたP4群の対称性を満たすための条件式をよく見てみると、これらの条件式の左辺に現れる\( \boldsymbol{x}_{m_1+1}, \cdots, \boldsymbol{x}_{2m_1}, \boldsymbol{x}_{2m_1+m_2+1}, \cdots, \boldsymbol{x}_{2m_1+2m_2}, \boldsymbol{x}_{2m_1+2m_2+m_3}, \cdots, \boldsymbol{x}_{2m_1+2m_2+2m_3-1} \)の\(\frac{n}{2}\)個の座標位置は、右辺に現れる\( \boldsymbol{x}_{0}, \cdots, \boldsymbol{x}_{m_1}, \boldsymbol{x}_{2m_1+1}, \cdots, \boldsymbol{x}_{2m_1+m_2}, \boldsymbol{x}_{2m_1+2m_2+1}, \cdots, \boldsymbol{x}_{2m_1+2m_2+m_3-1} \)の\(\frac{n}{2}\)個の座標位置で表現されていることが分かります。そこで、\(n\)次元ベクトル\( \boldsymbol{z} \)を
\[ \boldsymbol{z} = ( x_0, y_0, \cdots, x_{m_1}, y_{m_1}, x_{2m_1+1}, y_{2m_1+1}, \cdots, x_{2m_1+m_2}, y_{2m_1+m_2}, x_{2m_1+2m_2+1}, y_{2m_1+2m_2+1}, \cdots, x_{2m_1+2m_2+m_3-1}, y_{2m_1+2m_2+m_3-1} )^t \]
とすると、条件式は以下の1つの式で表すことができます。
\[ \boldsymbol{u} = G \boldsymbol{z} \]
ここで、\(G\)は\(2n \times n\)の行列で、条件式の右辺に出てくる係数をまとめたものになります。
得られた係数行列\(G\)については今後の計算を簡単にするために、グラム・シュミットの直交化法を用いてもう少し変形しておきます。行列\(G\)を\(n\)個の\(2n\)次元ベクトルで表すことにします。
\[ G = ( \boldsymbol{g}_0, \boldsymbol{g}_1, \cdots , \boldsymbol{g}_{n-1} ) \]
これら\(n\)個の\(2n\)次元ベクトル\( \boldsymbol{g}_i \ \ (i=0,1,\cdots, n-1) \)を正規直交基底\( \bar{\boldsymbol{g}}_i \ \ (i=0,1,\cdots, n-1) \)に次の手順(グラム・シュミットの直交化法)で変更していきます。
\[ \bar{\boldsymbol{g}}_0 = \frac{ \boldsymbol{g}_0 }{ | \boldsymbol{g}_0 | }, \ \ \bar{\boldsymbol{g}}_i = \frac{ \boldsymbol{g}_i – \sum_{j=0}^{i-1} ( \boldsymbol{g}_i \cdot \bar{\boldsymbol{g}}_j ) \bar{\boldsymbol{g}}_j }{ \left| \boldsymbol{g}_i – \sum_{j=0}^{i-1} ( \boldsymbol{g}_i \cdot \bar{\boldsymbol{g}}_j ) \bar{\boldsymbol{g}}_j \right| } \ \ (i=1, \cdots, n-1 ) \]
これらの正規直交基底\( \bar{\boldsymbol{g}}_i \ \ (i=0,1,\cdots, n-1) \)を用いて、変形した係数行列\(\bar{G}\)を
\[ \bar{G} = ( \bar{\boldsymbol{g}}_0, \bar{\boldsymbol{g}}_1, \cdots , \bar{\boldsymbol{g}}_{n-1} ) \]
とおくと、条件式は
\[ \boldsymbol{u} = \bar{G} \bar{\boldsymbol{z}} \]
と変形することができます。ここで、\(\bar{\boldsymbol{z}}\)は\( G \boldsymbol{z} = \bar{G} \bar{\boldsymbol{z}} \)となるように、\(\boldsymbol{z}\)を変数変換したものになります。
以上で、準備が整いました。最後に、変形した条件式を\(F\)に代入して、
\[ F = (\bar{G} \bar{\boldsymbol{z}} – \boldsymbol{w})^t \cdot (\bar{G} \bar{\boldsymbol{z}} – \boldsymbol{w}) \]
とすると、この\(F\)が最小になるように変数\(\bar{\boldsymbol{z}}\)を選ぶことで元の図形の\(n\)角形にできるだけ同じ形になるような基本図形の変形を行うことができます。実際、\(F\)が最小になるのは、
\[ \bar{z} = \bar{G}^t \boldsymbol{w} \]
のときとなり、したがって、 元の図形の\(n\)角形にできるだけ同じ形になるような基本図形の頂点位置\(\bar{u}\)は
\[ \bar{u} = \bar{G} \bar{G}^t \boldsymbol{w} \]
で得られることが分かります。
なお、ここで紹介した変形した基本図形の頂点座標の計算方法は、書籍「エッシャー・マジック―だまし絵の世界を数理で読み解く」の第4章に解説が載っていますので、より詳しく知りたい方はそちらを参考にしてください。
この方法で算出した、変形後の基本図形は以下のようになりました(赤:元の図形、青:基本図形(変形前)、緑:基本図形(変形後))。

変形した基本図形を壁紙群の対称性に合わせて並べていく
ここまで準備が整えば、後はP4群の対称性に合わせて変形後の基本図形を並べていくだけですが、最後に変形後の基本図形を正方格子のサイズに合わせて、リサイズを行っておきます。
ポイントとしては、
・基本図形の辺\(a\)と辺\(b\)が交わる点(\(m_1\)番目の点)が正方格子を表す格子点と一致すること
・基本図形の辺\(c\)と辺\(d\)が交わる点(\(2m_1+m_2\)番目の点)が正方格子が形作る正方形の重心と一致すること
・基本図形の辺\(e\)の中点(\(2m_1+2m_2+m_3\)番目の点)が正方格子が形作る一辺の中点と一致すること
が挙げられます。以上の対応関係を利用することで、基本図形のサイズを適切に調整することができます。
このリサイズを行った後、変形後の基本図形をP4群の対称性に合わせて並べていくことで、下記のようなエッシャー風の絵を形作ることができます。

プログラムコード
最後に、今回のエッシャー風の絵を描くためのプログラムコードをまとめておきます。
なお、今回の絵を作成するためのプログラムコードは、別記事「渦巻き図形(P4)」に記載しているプログラムコードのうち、makeRecurSquare関数を下記のmakeFundamentalFigure関数に置き換えたものになります。(もう少し細かい話をすると、makeTileP4関数内のmakeRecurSquare関数をmakeFundamentalFigure関数に変更する必要があります。また、drawTiling関数内の記述していた「格子点を描く」部分はコメントアウトしています。)
あと、今回の元の図形(牛の図形)の画像ファイルを「cow.jpg」としてpdeファイルのフォルダに入れておく必要があります。
import gab.opencv.*;
// 画像をP4群の基本図形となるように変形する関数(基本図形)
PShape makeFundamentalFigure(){
OpenCV cv;
PImage im, th;
ArrayList<Contour> contours; // 輪郭点を格納する変数
int m1 = 23; // 辺aと辺b上の輪郭点の数
int m2 = 21; // 辺cと辺d上の輪郭点の数
int m3 = 60-m1-m2; // 辺e上の輪郭点の数の半分
int m = m1+m2+m3;
int n = 2*m; // 全輪郭点の数
// ベクトルを反時計回りに90°回転させるための行列の成分
float r90_12 = -1.0;
float r90_21 = 1.0;
// 画像の読み込み
im = loadImage("cow.jpg");
// OpenCVを用いて輪郭を抽出する
cv = new OpenCV(this,im);
// グレースケール変換
cv.gray();
// 2値化
cv.threshold(150);
// 2値画像から輪郭抽出
contours = cv.findContours();
// 輪郭抽出(n個の点を抽出する)
float[] w = new float[2*n];
for (Contour contour : contours) {
int contour_point_num = contour.numPoints();
float delta = (float)contour_point_num/n;
ArrayList<PVector> p2 = contour.getPoints();
int number = 0;
for(int i=0; i<n; i++){
number = round(delta*i);
w[2*i] = p2.get(number).x;
w[2*i+1] = p2.get(number).y;
}
}
// 配列gの初期化
float[][] g = new float[2*n][2*m];
for(int i=0; i<2*n; i++){
for(int j=0; j<2*m; j++){
g[i][j] = 0.0;
}
}
// 0列目
g[0][0] = 1.0;
g[1][1] = 1.0;
g[2*(2*m1)+1][0] = r90_21;
g[2*(2*m1)][1] = r90_12;
g[2*(2*m1+2*m2)][0] = -1.0;
g[2*(2*m1+2*m2)+1][1] = -1.0;
// 1~m1-1列目
for(int i=1; i<m1; i++){
g[2*i][2*i] = 1.0;
g[2*i+1][2*i+1] = 1.0;
g[2*(2*m1-i)+1][2*i] = r90_21;
g[2*(2*m1-i)][2*i+1] = r90_12;
}
// m1列目
g[2*m1][2*m1] = 1.0;
g[2*m1+1][2*m1+1] = 1.0;
for(int i=m1+1; i<2*m1+1; i++){
g[2*i][2*m1] = 1.0;
g[2*i+1][2*m1+1] = 1.0;
g[2*i+1][2*m1] = -r90_21;
g[2*i][2*m1+1] = -r90_12;
}
g[2*(2*m1+2*m2)][2*m1] = 1.0;
g[2*(2*m1+2*m2)+1][2*m1+1] = 1.0;
g[2*(2*m1+2*m2)+1][2*m1] = r90_21;
g[2*(2*m1+2*m2)][2*m1+1] = r90_12;
g[2*(2*m1+2*m2+m3)][2*m1] = 0.5;
g[2*(2*m1+2*m2+m3)+1][2*m1+1] = 0.5;
g[2*(2*m1+2*m2+m3)+1][2*m1] = 0.5*r90_21;
g[2*(2*m1+2*m2+m3)][2*m1+1] = 0.5*r90_12;
for(int i=2*m1+2*m2+m3+1; i<2*m1+2*m2+2*m3; i++){
g[2*i][2*m1] = 1.0;
g[2*i+1][2*m1+1] = 1.0;
g[2*i+1][2*m1] = r90_21;
g[2*i][2*m1+1] = r90_12;
}
// m1+1~m1+m2-1列目
for(int i=1; i<m2; i++){
g[2*(2*m1+i)][2*(m1+i)] = 1.0;
g[2*(2*m1+i)+1][2*(m1+i)+1] = 1.0;
g[2*(2*m1+2*m2-i)+1][2*(m1+i)] = r90_21;
g[2*(2*m1+2*m2-i)][2*(m1+i)+1] = r90_12;
}
// m1+m2列目
g[2*(2*m1+m2)][2*(m1+m2)] = 1.0;
g[2*(2*m1+m2)+1][2*(m1+m2)+1] = 1.0;
for(int i=2*m1+m2+1; i<2*m1+2*m2+1; i++){
g[2*i][2*(m1+m2)] = 1.0;
g[2*i+1][2*(m1+m2)+1] = 1.0;
g[2*i+1][2*(m1+m2)] = -r90_21;
g[2*i][2*(m1+m2)+1] = -r90_12;
}
g[2*(2*m1+2*m2+m3)][2*(m1+m2)] = 0.5;
g[2*(2*m1+2*m2+m3)+1][2*(m1+m2)+1] = 0.5;
g[2*(2*m1+2*m2+m3)+1][2*(m1+m2)] = -0.5*r90_21;
g[2*(2*m1+2*m2+m3)][2*(m1+m2)+1] = -0.5*r90_12;
for(int i=2*m1+2*m2+m3+1; i<2*m1+2*m2+2*m3; i++){
g[2*i][2*(m1+m2)] = 1.0;
g[2*i+1][2*(m1+m2)+1] = 1.0;
g[2*i+1][2*(m1+m2)] = -r90_21;
g[2*i][2*(m1+m2)+1] = -r90_12;
}
// m1+m2+1~m1+m2+m3-1列目
for(int i=1; i<m3; i++){
g[2*(2*m1+2*m2+i)][2*(m1+m2+i)] = 1.0;
g[2*(2*m1+2*m2+i)+1][2*(m1+m2+i)+1] = 1.0;
g[2*(2*m1+2*m2+2*m3-i)][2*(m1+m2+i)] = -1.0;
g[2*(2*m1+2*m2+2*m3-i)+1][2*(m1+m2+i)+1] = -1.0;
}
// 行列gを正規直交基底にする(グラム・シュミットの直交化法)
float g_size;
float[] inner_product = new float[2*m];
float[][] g_temp = new float[2*n][2*m];
for(int i=0; i<2*m; i++){
for(int j=0; j<i; j++){
inner_product[j] = 0.0;
for(int k=0; k<2*n; k++){
inner_product[j] += g[k][i]*g[k][j];
}
for(int k=0; k<2*n; k++){
g_temp[k][j] = inner_product[j]*g[k][j];
}
}
for(int j=0; j<i; j++){
for(int k=0; k<2*n; k++){
g[k][i] -= g_temp[k][j];
}
}
g_size =0.0;
for(int j=0; j<2*n; j++){
g_size += g[j][i]*g[j][i];
}
g_size = sqrt(g_size);
for(int j=0; j<2*n; j++){
g[j][i] /= g_size;
}
}
// 最適な図形を探索する
float F;
float F_min = 1.0*pow(10.0,36.0);
float[] z = new float[2*m];
float[] u = new float[2*n];
float[] u_min = new float[2*n];
int g_rotation_num_min = 0;
int g_rotation_num = 0;
while( g_rotation_num < n ){
for(int i=0; i<2*m; i++){
z[i] = 0.0;
for(int j=0; j<2*n; j++){
z[i] += g[j][i]*w[j];
}
}
for(int i=0; i<2*n; i++){
u[i] = 0.0;
for(int j=0; j<2*m; j++){
u[i] += g[i][j]*z[j];
}
}
F = 0.0;
for(int i=0; i<2*n; i++){
F += (u[i]-w[i])*(u[i]-w[i]);
}
if(F < F_min){
F_min = F;
g_rotation_num_min = g_rotation_num;
for(int i=0; i<2*n; i++){
u_min[i] = u[i];
}
}
// gを更新
float[] g_last_x = g[0];
float[] g_last_y = g[1];
for(int i=1; i<n; i++){
g[2*(i-1)] = g[2*i];
g[2*(i-1)+1] = g[2*i+1];
}
g[2*(n-1)] = g_last_x;
g[2*(n-1)+1] = g_last_y;
g_rotation_num++;
}
// 正方格子上の点m1の位置を取得する
PVector origin = new PVector();
origin.x = u_min[2*((n-g_rotation_num_min+m1)%n)];
origin.y = u_min[2*((n-g_rotation_num_min+m1)%n)+1];
// 隣り合う正方格子点の中点上の点m3の位置を取得する
PVector baseline = new PVector();
baseline.x = u_min[2*((n-g_rotation_num_min+2*m1+2*m2+m3)%n)];
baseline.y = u_min[2*((n-g_rotation_num_min+2*m1+2*m2+m3)%n)+1];
// 図形を正方格子のサイズにリサイズする
float p4_resize = (scalar/2.0)/baseline.copy().sub(origin.copy()).mag();
for(int i=0; i<n; i++){
u_min[2*i] -= origin.x;
u_min[2*i] *= p4_resize;
u_min[2*i+1] -= origin.y;
u_min[2*i+1] *= p4_resize;
}
// 最後に元の正方格子にあうように回転する
float theta = atan2(baseline.y-origin.y, baseline.x-origin.x);
for(int i=0; i<n; i++){
u[2*i] = u_min[2*i] * cos(-theta) - u_min[2*i+1] * sin(-theta);
u[2*i+1] = u_min[2*i] * sin(-theta) + u_min[2*i+1] * cos(-theta);
}
// 算出された輪郭点を順に結んで図形を形作る
PShape transformed_cow = createShape();
transformed_cow.beginShape();
for(int i=0; i<n; i++){
transformed_cow.vertex(u[2*i],u[2*i+1]);
}
transformed_cow.endShape(CLOSE);
return transformed_cow;
}