カワウの模様

ここでは、書籍「M.C.エッシャーと楽しむ算数・数学パズル」のp.155に紹介されている「カワウの模様」をProcessingで再現してみましたので、その描き方とともに解説したいと思います。

Contents

1 カワウの模様
2 描き方
- 2.1 基本図形の並べ方
- 2.2 カワウの模様の基本図形の準備
3 プログラムコード

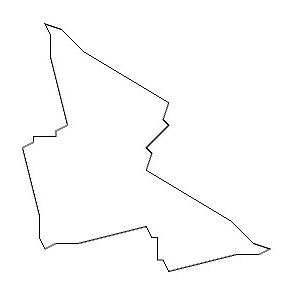
今回描いてみたカワウの模様は以下のような図形になりました。

描き方

今回描いたカワウの模様の基本図形は以下のようなものになります。

このカワウの模様の基本図形は、直角二等辺三角形を準備して各辺を変形することで作ることができます。

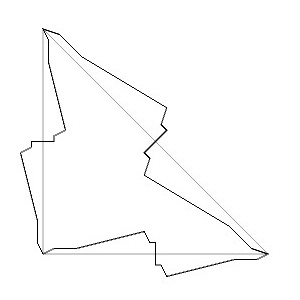
この変形のやり方を説明する前に、まずこれらの基本図形の並べ方についてみていきます。

基本図形の並べ方

カワウの模様は17種類の壁紙群のいずれにも当てはまりません。そのため、基本図形の並べ方を考える必要があります。今回は、以下に説明するように並べています。なお、ここでは基本図形を直角二等辺三角形として考えます。

この模様を描く手順を考えていきます。

まず一番外側にある同じ大きさの8個の直角二等辺三角形（下図の赤枠で囲んだ部分）に注目します。この直角二等辺三角形と全体の正方形との大きさを比べてみると、直角二等辺三角形の隣辺（斜辺ではない辺のこと）の長さは正方形の中心から正方形の一つの頂点までの長さ（青色の線分）の半分であることが分かります。したがって、隣辺の長さが青色の線分の長さの半分となるような直角二等辺三角形を準備して、配色を調整しながら図のように並べていきます。

次に、二番目に外側にある同じ大きさの8個の直角二等辺三角形（下図の赤枠で囲んだ部分）に注目します。二番目に外側にある直角二等辺三角形と一番外側にある直角二等辺三角形とを比べてみると、二番目に外側にある直角二等辺三角形の斜辺の長さと一番外側にある直角二等辺三角形の隣辺の長さが一致していることが分かります。つまり、二番目に外側にある直角二等辺三角形の隣辺の長さは一番外側の直角二等辺三角形の長さを\(1/\sqrt{2}\)倍したものになります。したがって、隣辺の長さを一番外側の直角二等辺三角形の隣辺の\(1/\sqrt{2}\)倍になるような直角二等辺三角形を準備して、配色を調整しながら図のように並べていきます。

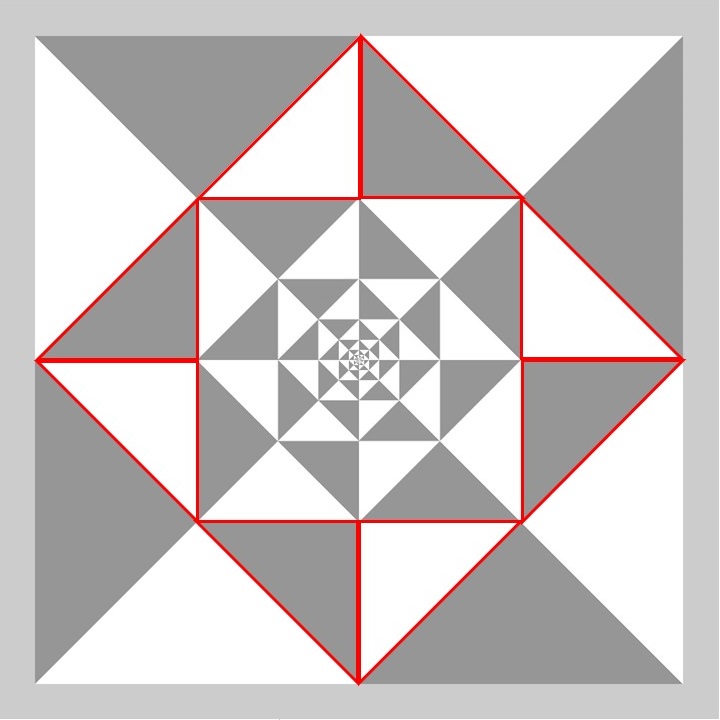
以上の手順を三番目に外側にある直角二等辺三角形、四番目に外側にある直角二等辺三角形と繰り返し描いていくことで、求めたい模様を描くことができます。

カワウの模様の基本図形の準備

次に、直角二等辺三角形を変形してカワウの模様の基本図形を得るために、各直角二等辺三角形にラベルをふり、隣り合う基本図形同士の辺のラベルと向きの対応をみてみます。

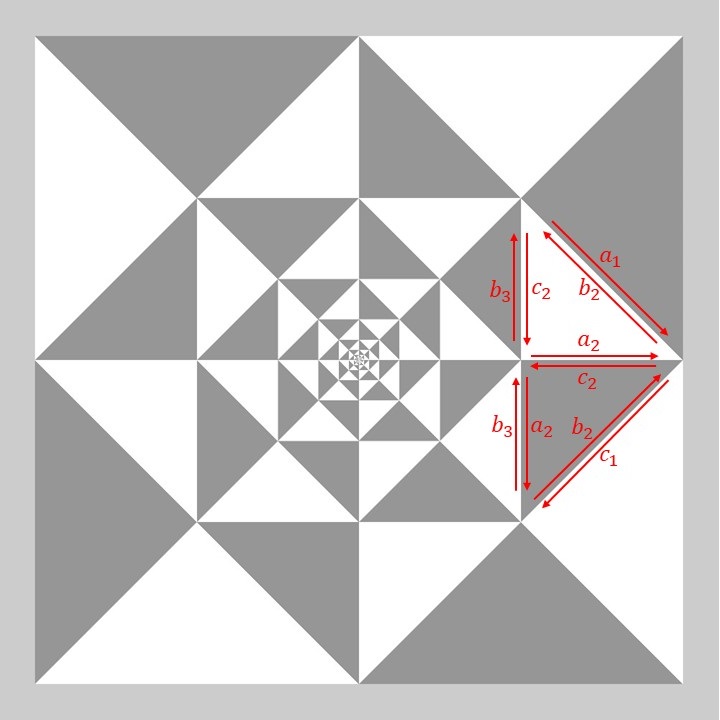
各辺のラベルは一番外側の直角二等辺三角形についてラベルの添え字に\(1\)を、二番目に外側の直角二等辺三角形についてラベルの添え字に\(2\)を、という順番でつけています。

まず、二番目に外側の直角二等辺三角形同士が共有している辺\(a_2,c_2\)に注目してみます。辺\(a_2\)と辺\(c_2\)は互いに反対の向きに重なっています。つまり、辺\(a_2\)を適当に変形したあと、辺\(c_2\)は、変形した辺\(a_2\)を上下左右反転した形状に変形することができます。

次に、二番目に外側の直角二等辺三角形と三番目に外側の直角二等辺三角形とが共有している辺\(b_3\)と辺\(a_2\)、辺\(b_3\)と辺\(c_2\)の組合せに注目してみます。辺\(b_3\)と辺\(a_2\)は互いに反対の向きに重なっていますので、辺\(b_3\)を適当に変形したあと、辺\(a_2\)は、変形した辺\(b_3\)を上下左右反転した形状に変形することができます。また、辺\(b_3\)と辺\(c_2\)も互いに反対の向きに重なっていますので、辺\(b_3\)を適当に変形したあと、辺\(c_2\)は、変形した辺\(b_3\)を上下左右反転した形状に変形することができます。つまり、辺\(a_2\)と辺\(c_2\)は共に、変形した辺\(b_3\)を上下左右反転した形状となるので、辺\(a_2\)と辺\(c_2\)は同じ形状になる必要があります。

以上のことから、辺\(a_2\)と辺\(c_2\)は同じ形状でかつ片方を上下左右反転しても一致するような形状、すなわち、辺の中点に関して点対称な形状になることが分かります。また、これにともない辺\(b_3\)も辺\(a_2\)、辺\(c_2\)と同じ中点に関して点対称な形状となります。

まとめると、辺\(a_i\)と辺\(c_i\)および辺\(b_{i+1}\)は同じ形状で中点に関して点対称な変形をすることができます。

なお、今回はすべての辺に対して以下のような中点に関して点対称な変形を行っています。

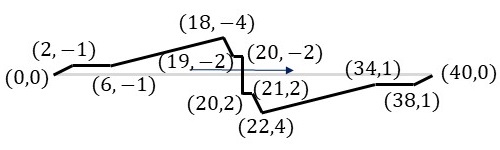
これらの変形を実施した結果、直角二等辺三角形はカワウの模様の基本図形に変形することができます。

プログラムコード

カワウの模様の基本図形を上記で記載した「基本図形の並べ方」の手順で並べていくと、最初に示したような図形を得ることができます。

void setup(){

  size(1000, 1000, P2D);
  float max_size = width * 9.0 / 20.0;

  translate(width/2, height/2);
  drawTiling(max_size);
  
  save("cormorants.jpg");
}

// 二等辺三角形を変形する関数（基本図形）
PShape transformTriangle(
  float s
){
  PVector[] v = new PVector[3]; // 二等辺三角形の頂点

  v[0] = new PVector(0.0,0.0);
  v[1] = new PVector(1.0,0.0);
  v[1].mult(s);
  v[2] = new PVector(0.0,1.0);
  v[2].mult(-s);

  // 変形した二等辺三角形を描く
  PShape tri = createShape();
  tri.beginShape(); 
  PVector[] auxiliary_point;
  // 辺aの変形
  tri.vertex(v[0].x, v[0].y);
  auxiliary_point = getAuxiliaryPoints(v[0], v[1]);
  for(int i=0; i<10; i++){
    tri.vertex(auxiliary_point[i].x, auxiliary_point[i].y);
  }
  tri.vertex(v[1].x, v[1].y); 
  // 辺bの変形
  auxiliary_point = getAuxiliaryPoints(v[1], v[2]);
  for(int i=0; i<10; i++){
    tri.vertex(auxiliary_point[i].x, auxiliary_point[i].y);
  }
  tri.vertex(v[2].x, v[2].y); 
  // 辺cの変形
  auxiliary_point = getAuxiliaryPoints(v[2], v[0]);
  for(int i=0; i<10; i++){
    tri.vertex(auxiliary_point[i].x, auxiliary_point[i].y);
  }
  tri.vertex(v[0].x, v[0].y); 

  tri.endShape();
  
  return tri;
}

PVector[] getAuxiliaryPoints(
  PVector v1,
  PVector v2
){
  PVector[] auxiliary_point = new PVector[10];
  auxiliary_point[0] = getAuxiliaryPoint(v1, v2, 2.0/40.0, -1.0/40.0);
  auxiliary_point[1] = getAuxiliaryPoint(v1, v2, 6.0/40.0, -1.0/40.0);
  auxiliary_point[2] = getAuxiliaryPoint(v1, v2, 18.0/40.0, -4.0/40.0);
  auxiliary_point[3] = getAuxiliaryPoint(v1, v2, 19.0/40.0, -2.0/40.0);
  auxiliary_point[4] = getAuxiliaryPoint(v1, v2, 20.0/40.0, -2.0/40.0);
  auxiliary_point[5] = getAuxiliaryPoint(v1, v2, 20.0/40.0, 2.0/40.0);
  auxiliary_point[6] = getAuxiliaryPoint(v1, v2, 21.0/40.0, 2.0/40.0);
  auxiliary_point[7] = getAuxiliaryPoint(v1, v2, 22.0/40.0, 4.0/40.0);
  auxiliary_point[8] = getAuxiliaryPoint(v1, v2, 34.0/40.0, 1.0/40.0);
  auxiliary_point[9] = getAuxiliaryPoint(v1, v2, 38.0/40.0, 1.0/40.0);

  return auxiliary_point;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

// タイルを生成する関数
PShape makeTilePGG(
  float s
){
  PShape tile;
  tile = createShape(GROUP); // PShapeのグループを作る
  for(int i=0; i<2; i++){

    noStroke();
    if( i%2 == 0){
      fill(255,255,255);
    } else {
      fill(150,150,150);
    }
    
    PShape tri = transformTriangle(s); // 変形された二等辺三角形の生成
    tri.rotate(radians(90)*i);
    tile.addChild(tri); // グループに追加
  }
  
  return tile;
}

// 外側から順にタイリングを描画する関数
void drawTiling(
  float max_size
){
//  background(255);
  float s = max_size;
  PShape tile;
  for(int i=0; i<50; i++){
    s = s/sqrt(2.0);
    for(int j=0; j<4; j++){
      tile = makeTilePGG(s);
      tile.translate(s,0.0);
      tile.rotate(radians(90)*j+radians(45)*(1.0-i%2));

      shape(tile);
    }
  }
}