この記事では書籍「世界一美しい錯視アート」に掲載されている「手品師」という作品をProcessingを使って再現してみます。
手品師
今回作成した錯視アート「手品師」です。

書籍では「ぎらぎらして見える。」と解説されています。自分にはなんとなく黄色が強く見えます。
描き方のポイント
三角形を円形に並べた図形を縮小、回転させて描いていく
最初、これまで通り動径方向に三角形を並べた図形を用意して、これを回転させながら配置していくことを考えましたが、動径方向をよくみると、各角度方向で三角形の色の順番が異なっている(パターンを指定しにくい)ことがわかりました。一方で、円形上の三角形の並びに関しては時計回りに「黄色+黄色」「紫色+白色」「青色+赤色」「白色+緑色」の順になっていることが分かります。
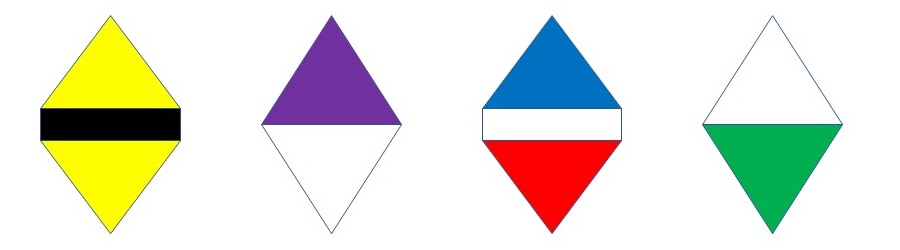
そこで、今回は三角形を円形に並べた図形を円の半径の縮小に合わせて回転させながら描いていくことにしました。なお、回転方向は縮小を4回したら、次は回転方向を逆向きにするという処理を繰り返すことで図形をかみなり型に配置することができます。
縮小比率をどう取るか
この作品「手品師」を再現する上でのもう一つのポイントは円の縮小比率をどう取っていくかになります。ここでは、動径方向に並んだ三角形の大きさから縮小比率を算出していきたいと思います。
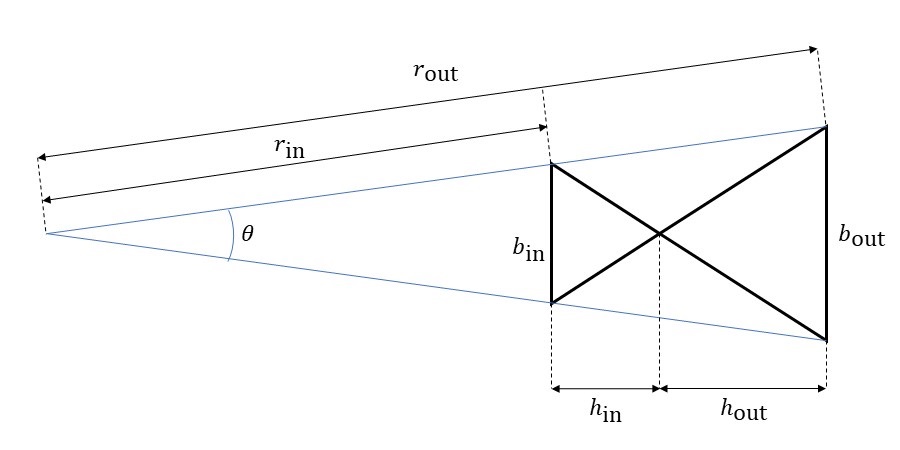
縮小比率を\(\alpha \)とおきます。このとき、上図のようにパラメータを設定すると\[ r_{\rm{in}}= \alpha r_{\rm{out}}, \ \ h_{\rm{in}}= \alpha h_{\rm{out}} \]となります。一方、三角形は円形に72個並んでいるので、\[ \theta = \frac{360^\circ}{72} = 5^\circ \]となります。これらの三角形は正三角形であると考えると、その一辺の長さは\[ b_{\rm{out}} = 2 r_{\rm{out}} \sin \frac{\theta}{2}, \ \ b_{\rm{in}} = 2 r_{\rm{in}} \sin \frac{\theta}{2} \]で計算することができます。したがって、三角形の高さは\[ h_{\rm{out}}=\sqrt{3} r_{\rm{out}} \sin \frac{\theta}{2}, \ \ h_{\rm{in}}=\sqrt{3} r_{\rm{in}} \sin \frac{\theta}{2} \]となります。 これらのパラメータ間には\[ r_{\rm{out}} \cos \frac{\theta}{2} – r_{\rm{in}} \cos \frac{\theta}{2} = h_{\rm{out}}+h_{\rm{in}} \]という関係が成り立つので、この式から縮小比率\(\alpha \)は\[ \alpha = \frac{\cos \frac{\theta}{2} – \sqrt{3} \sin \frac{\theta}{2} }{ \cos \frac{\theta}{2} + \sqrt{3} \sin \frac{\theta}{2} } \]となります。
プログラムコード
今回作成した錯視アート「手品師」のプログラムコードを載せておきます。
void setup() {
size(1000, 1000);
background(0,0,0);
noStroke();
translate(width/2, height/2);
float x0 = width/2.0 - width/30.0; // 一番外側の円の半径
int triangles_num = 72; // 円上に並ぶ三角形の数
float theta = radians(360.0/triangles_num); // 三角形1つ分の中心角の角度
float ratio = (cos(theta/2.0) - sqrt(3.0)*sin(theta/2.0))/(cos(theta/2.0) + sqrt(3.0)*sin(theta/2.0)); // 縮小比率
int i = 0;
float x = x0;
while(i < 25){ // 25個の円を描く
drawTriangles(x, triangles_num, theta);
if( i%8 < 4 ){ // 円4つずつで回転方向を変える
rotate(theta);
} else {
rotate(-theta);
}
x = x * ratio;
i++;
}
save("magician.jpg");
}
// 円上に三角形を並べた図形を描く関数
void drawTriangles(
float xs, // 円の半径
int triangles_num, // 並べる三角形の数
float theta // 円の中心での角度
){
float x;
float y;
x = xs * cos(theta/2.0);
y = xs * sin(theta/2.0);
for(int i=0; i<triangles_num; i++){
noStroke();
if (i%4 == 0){ // 2つの黄色の三角形の間に黒色の矩形が入った図形
fill(255,255,0);
triangle(x+y*sqrt(3.0)/10.0, y, x+y*sqrt(3.0)/10.0, -y, x+y*sqrt(3.0), 0.0);
triangle(x-y*sqrt(3.0)/10.0, y, x-y*sqrt(3.0)/10.0, -y, x-y*sqrt(3.0), 0.0);
fill(0,0,0);
rectMode(CENTER);
rect(x, 0.0, y*sqrt(3.0)/5.0, y*2.0);
} else if ( i%4 == 1 ) { // 紫色と白色の三角形
fill(255,0,255);
triangle(x, y, x, -y, x+y*sqrt(3.0), 0.0);
fill(255,255,255);
triangle(x, y, x, -y, x-y*sqrt(3.0), 0.0);
} else if ( i%4 == 2 ) { // 青色と赤色の三角形の間に白色の矩形が入った図形
fill(0,0,255);
triangle(x+y*sqrt(3.0)/10.0, y, x+y*sqrt(3.0)/10.0, -y, x+y*sqrt(3.0), 0.0);
fill(255,0,0);
triangle(x-y*sqrt(3.0)/10.0, y, x-y*sqrt(3.0)/10.0, -y, x-y*sqrt(3.0), 0.0);
fill(255,255,255);
rectMode(CENTER);
rect(x, 0.0, y*sqrt(3.0)/5.0, y*2.0);
} else { // 白色と緑色の三角形
fill(255,255,255);
triangle(x, y, x, -y, x+y*sqrt(3.0), 0.0);
fill(0,255,0);
triangle(x, y, x, -y, x-y*sqrt(3.0), 0.0);
}
rotate(theta);
}
}