この記事では書籍「世界一美しい錯視アート」に掲載されている「冷却水」という作品をProcessingを使って再現してみます。
冷却水
今回作成した錯視アート「冷却水」です。

書籍では「リングの中を何かが走っているように見える。」と解説されています。確かに、何かが走ります。
描き方のポイント
青色の円を基準にして描いていく
この作品「冷却水」をどのように描いていくかを考えたときにまず浮かんだのが、半径の縮小比率を適当に調整して青色の円と黄色の円を交互に描いていく、というものでした。でも作品をよく見てみると、青色の円から外側に出ているとげとげの高さと内側に出ているとげとげの高さは同じ高さになっているようですので、どうも縮小比率を指定して青色の円と黄色の円を交互に描いていく方法では再現できないことがわかりました。
そこで、今回は次のように青色の円を基準として描いていくことにしました。
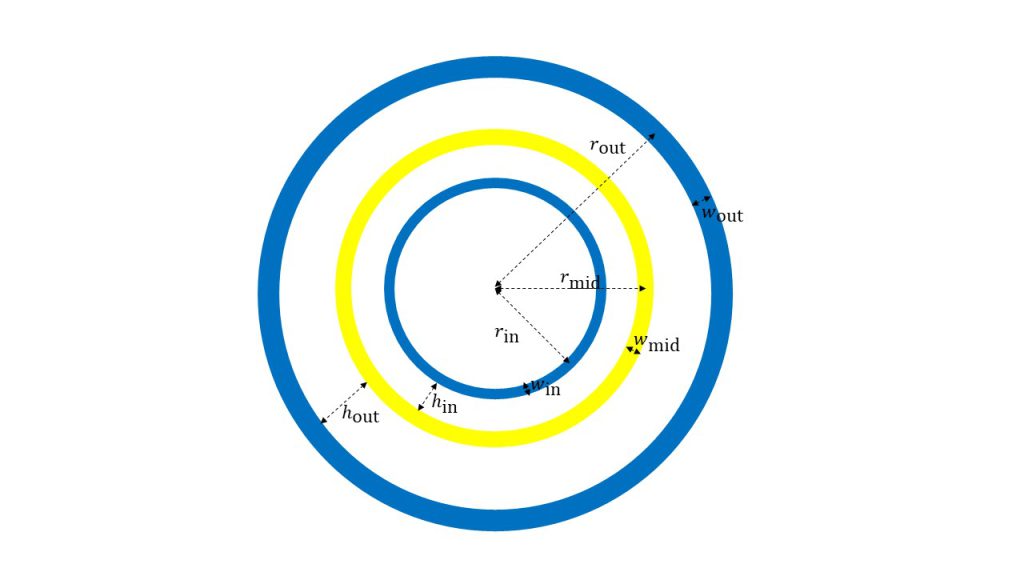
外側の青色の円の半径と幅を決めて描く
まず外側の青色の円の半径\(r_{\rm{out}}\)、幅\(w_{\rm{out}}\)を決めて、外側の青色の円を描きます。
縮小比率を決めて内側の青色の円を描く
次に縮小比率を\(\alpha\)とすると、内側の青色の円の半径\(r_{\rm{in}}\)、幅\(w_{\rm{in}}\)は \[ r_{\rm{in}}=\alpha r_{\rm{out}}, \ \ w_{\rm{in}}=\alpha w_{\rm{out}} \]となるので、この値で内側の青色の円を描いていきます。
とげの高さを計算して描いていく
外側の青色の円と内側の青色の円に挟まれる黄色の円の幅\(w_{\rm{mid}}\)は外側の青色の円と内側の青色の円の幅の平均値であると考えると、 \[ w_{\rm{mid}}=\frac{ w_{\rm{out}}+w_{\rm{in}} }{2} \]となります。また、外側の青色の円から出ているとげの高さを\(h_{\rm{out}}\)、内側の青色の円から出ているとげの高さを \(h_{\rm{in}}\) とすると\[ h_{\rm{in}}=\alpha h_{\rm{out}} \]となります。さらに、関係式\[ r_{\rm{out}}= r_{\rm{in}}+\frac{w_{\rm{in}}}{2}+h_{\rm{in}}+w_{\rm{mid}}+h_{\rm{out}}+\frac{w_{\rm{out}}}{2} \]が成り立ちますので、これまで出てきた式をまとめると\[ h_{\rm{out}}=\frac{ (1-\alpha) r_{\rm{out}}-(1+\alpha) w_{\rm{out}} }{1+\alpha} \]となります。 以上のことから、とげの高さが計算できましたので、外側の青色の円から出ているとげと内側の青色の円から出ているとげを描くことができます。
黄色の円の半径を計算して描いていく
最後に、黄色の円の半径\( r_{\rm{mid}}\)は\[ r_{\rm{mid}}=r_{\rm{out}}-\frac{w_{\rm{out}}}{2}-h_{\rm{out}}- \frac{w_{\rm{mid}}}{2} \]で計算することができます。黄色の円の幅\(w_{\rm{mid}}\)は上記で計算しているので、これらの値を使って黄色の円を描くことができます。
なお、これらの処理を青色の円を縮小させながら繰り返していきますが、3回目に描くときは黄色ではなく赤色の円を描きます。
中心は紫色の円形グラデーション
中心部分は紫色で円形にグラデーションしたものになっています。円形のグラデーションを描く方法は別記事「円形のグラデーションを描く」を見てください。
プログラムコード
今回作成した錯視アート「冷却水」のプログラムコードを載せておきます。
void setup() {
size(1000, 1000, P2D);
background(255,255,255);
noStroke();
translate(width/2, height/2);
float x0 = width/2.0 - width/8.0; // 一番外側の青色の円の半径
float w0 = width/40.0; // 一番外側の青色の円の幅
float ratio = 1.0/2.0; // 一番外側の青色の円と二番目の青色の円の大きさの比率
// とげとげを描く
int line_num = 120;
for(int i=0; i<line_num; i++){
rotate(radians(360.0/line_num));
drawTriangles(x0, w0, ratio, radians(360.0/120.0/2.0));
}
// 円形のグラデーションを描く
drawCircles(x0, w0, ratio);
save("reikyakusui.jpg");
}
// 青色の円から出ているとげとげを描く関数
void drawTriangles(
float xs, // 外側の青色の円の半径
float ws, // 外側の青色の円の幅
float ratio, // 縮小比率
float theta // 分割の角度
){
float x_out; // 外側の円の半径(青い円)
float x_mid; // 中間の円の半径(黄色または赤い円)
float x_in; // 内側の円の半径(青い円)
float w_out; // 外側の円の幅(太さ)
float w_mid; // 中間の円の幅
float w_in; // 内側の円の幅
float r; // 縮小時の比率
float triangle_height; // 三角形の高さ
float x1, y1, x2, y2;
x_out = xs;
x_in = x_out * ratio;
w_out = ws;
w_in = w_out * ratio;
w_mid = (w_out + w_in)/2.0;
triangle_height = ((1.0 - ratio) * x_out - w_out - w_in)/(1.0+ratio);
x_mid = x_out - w_out/2.0 - triangle_height - w_mid/2.0;
int i = 0;
while(i<3){
x1 = (x_out + w_out/2.0) * cos(theta);
y1 = (x_out + w_out/2.0) * sin(theta);
x2 = (x_out - w_out/2.0) * cos(theta);
y2 = (x_out - w_out/2.0) * sin(theta);
noStroke();
fill(0,0,0);
triangle(x1, y1, x1, -y1, x_out + w_out/2.0 + triangle_height, 0.0);
triangle(x2, y2, x2, -y2, x_out - w_out/2.0 - triangle_height, 0.0);
x_out = x_in;
x_in = x_out * ratio;
w_out = w_in;
w_in = w_out * ratio;
w_mid = (w_out + w_in)/2.0;
triangle_height = ((1.0 - ratio) * x_out - w_out - w_in)/(1.0+ratio);
x_mid = x_out - w_out/2.0 - triangle_height - w_mid/2.0;
i++;
}
}
// 円を描いていく関数
void drawCircles(
float xs, // 外側の青色の円の半径
float ws, // 外側の青色の円の幅
float ratio // 縮小比率
){
int i = 0;
float x_out; // 外側の円の半径(青い円)
float x_mid; // 中間の円の半径(黄色または赤い円)
float x_in; // 内側の円の半径(青い円)
float w_out; // 外側の円の幅(太さ)
float w_mid; // 中間の円の幅
float w_in; // 内側の円の幅
float triangle_height; // 三角形の高さ
float center_gradcircle_radius = 0.0; // 中心位置の紫色の円形グラデーションの半径
x_out = xs;
x_in = x_out * ratio;
w_out = ws;
w_in = w_out * ratio;
w_mid = (w_out + w_in)/2.0;
triangle_height = ((1.0 - ratio) * x_out - w_out - w_in)/(1.0+ratio);
x_mid = x_out - w_out/2.0 - triangle_height - w_mid/2.0;
while(i<3){
noFill();
stroke(0,0,255);
strokeWeight(w_out);
circle(0,0,x_out*2.0);
stroke(255,255,0);
if( i == 2 ){
stroke(255, 0, 0);
center_gradcircle_radius = x_mid-w_mid/2.0;
}
strokeWeight(w_mid);
circle(0,0,x_mid*2.0);
x_out = x_in;
x_in = x_out * ratio;
w_out = w_in;
w_in = w_out * ratio;
w_mid = (w_out + w_in)/2.0;
triangle_height = ((1.0 - ratio) * x_out - w_out - w_in)/(1.0+ratio);
x_mid = x_out - w_out/2.0 - triangle_height - w_mid/2.0;
i++;
}
noStroke();
color col_out = color(#53005D); // 外側の色
color col_in = color(#F5A2FF); // 内側の色
grdCircle(0.0, 0.0, center_gradcircle_radius*2.0, col_out, col_in);
}
// 円形のグラデーションを描く関数
void grdCircle(
float x, // 円の中心位置のx座標
float y, // 円の中心位置のy座標
float d, // 一番外側の円の直径
color col_out, // 円形のグラデーションの一番外側の色
color col_in // 円形のグラデーションの一番内側の色
) {
float c = 100;
for (int i=0; i<c; i++) {
color col = lerpColor(col_out, col_in, i/c); // 円の色
float dd = lerp(d, 0.0, i/c); // 円の直径
noStroke();
fill(col);
ellipse(x, y, dd, dd); // 円を描く
}
}